Archive
Procedure nesting a once common idiom
Structured programming was a popular program design methodology that many developers/managers claimed to be using in the 1970s and 1980s. Like all popular methodologies, everybody had/has their own idea about what it involves, and as always, consultancies sprang up to promote their take on things. The 1972 book Structured programming provides a taste of the times.
The idea underpinning structured programming is that it’s possible to map real world problems to some hierarchical structure, such as in the image below. This hierarchy model also provided a comforting metaphor for those seeking to understand software and its development.

The disadvantages of the Structured programming approach (i.e., real world problems often have important connections that cannot be implemented using a hierarchy) become very apparent as programs get larger. However, in the 1970s the installed memory capacity of most computers was measured in kilobytes, and a program containing 25K lines of code was considered large (because it was enough to consume a large percentage of the memory available). A major program usually involved running multiple, smaller, programs in sequence, each reading the output from the previous program. It was not until the mid-1980s…
At the coding level, doing structured programming involves laying out source code to give it a visible structure. Code blocks are indented to show if/for/while nesting and where possible procedure/functions are nested within the calling procedures (before C became widespread, functions that did not return a value were called procedures; Fortran has always called them subroutines).
Extensive nesting of procedures/functions was once very common, at least in languages that supported it, e.g., Algol 60 and Pascal, but not Fortran or Cobol. The spread of C, and then C++ and later Java, which did not support nesting (supported by gcc as an extension, nested classes are available in C++/Java, and later via lambda functions), erased nesting from coding consideration. I started life coding mostly in Fortran, moved to Pascal and made extensive use of nesting, then had to use C and not being able to nest functions took some getting used to. Even when using languages that support nesting (e.g., Python), I have not reestablished by previous habit of using nesting.
A common rationale for not supporting nested functions/methods is that it complicate the language specification and its implementation. A rather self-centered language designer point of view.
The following Pascal example illustrates a benefit of being able to nest procedures/functions:
procedure p1; var db :array[db_size] of char; procedure p2(offset :integer); function p3 :integer; begin (* ... *) return db[offset]; end; begin var off_val :char; off_val=p3; (* ... *) end; begin (* ... *) p2(3) end; |
The benefit of using nesting is in not forcing the developer to have to either define db at global scope, or pass it as an argument along the call chain. Nesting procedures is also a method of information hiding, a topic that took off in the 1970s.
To what extent did Algol/Pascal developers use nested procedures? A 1979 report by G. Benyon-Tinker and M. M. Lehman contains the only data I am aware of. The authors analysed the evolution of procedure usage within a banking application, from 1973 to 1978. The Algol 60 source grew from 35,845 to 63,843 LOC (657 procedures to 967 procedures). A large application for the time, but a small dataset by today’s standards.
The plot below shows the number of procedures/functions having a particular lexical nesting level, with nesting level 1 is the outermost level (i.e., globally visible procedures), and distinct colors denoting successive releases (code+data):
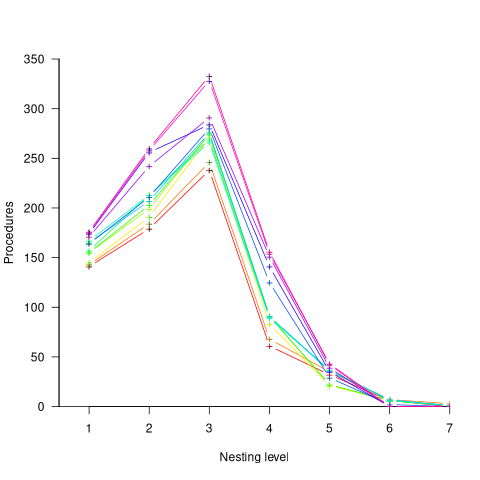
Just over 78% of procedures are nested within at least one other procedure. It’s tempting to think that nesting has a Poisson distribution, however, the distribution peaks at three rather than two. Perhaps it’s possible to fit an over-dispersed, but this feels like creating a just-so story.
What is the distribution of nested functions/methods in more recently written source? A study of 35 Python projects found 6.5% of functions nested and over twice as many (14.2%) of classed nested.
Are there worthwhile benefits to using nested functions/methods where possible, or is this once common usage mostly fashion driven with occasional benefits?
Like most questions involving cost/benefit analysis of language usage, it’s probably not sufficiently interesting for somebody to invest the effort required to run a reliable study.
21 Algol 60 compilers in 1962
The specification of ALGOL 60 was published in May 1960. Unlike today, where the creators of a new language release the source of a corresponding compiler, people were expected to write their own compiler. The June 1962 paper: The Replies to the AB14 Questionnaire lists implementation details on 21’ish compilers (it’s not clear whether some are dialects or languages very similar to Algol 60; 1963: list of 32 Algol compilers/versions).
Compiler writing was a hot leading edge research topic in the 1960s; at the start of this decade all the techniques we take for granted today had not yet been invented (Knuth invented LR parsing in 1965, and algorithms for optimal code generation started appearing in 1970). The 1960s was the period of the Cambrian explosion for programming languages.
Implementors not only had to deal with all the unknowns of writing a compiler, they also had to do the work using systems whose memory was measured in tens of kilobytes, computer interaction probably via punched card or punched tape, or if lucky, the luxury of teletype input/output. It’s no surprise that fourteen of the implementations considered themselves to be a “true subset” (which I take to mean that everything implemented was as per the specification). Compilers for earlier languages probably had the benefit of the language not supporting anything that was hard to implement.
Compiler implementation know-how received a major boost in 1964 with the publication of the book ALGOL 60 Implementation.
The plot below shows the number of compilers having a given reported implementation time (code+data):
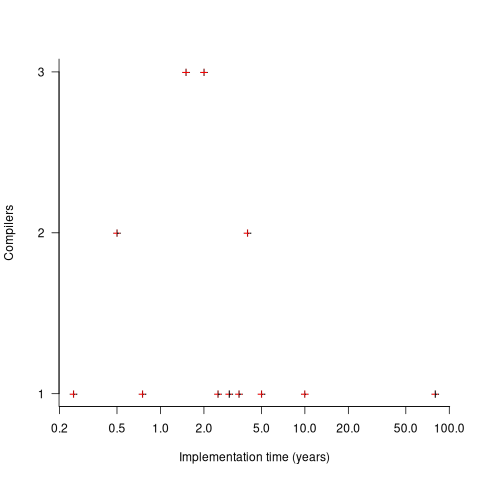
The median implementation effort is 2 man-years. Is this the result of a few good people working off the clock to create software, or management supporting the creation of a product that customers are not clamouring for?
The 0.25 man-year implementation looks like a port of an existing compiler to a different version of the same hardware. The 10 man-year implementation time was for what looks like a full implementation, plus extensions. The 80 man-year implementation time was reported by SDC (a large defence contractor) for a range of JOVIAL compilers (derived from Algol 58) targetting five different hardware platforms.
Were the implementors of Algol compilers different from the implementors of other languages? It’s not possible to say, although the language was created by a distinct group of people. The definition of Algol 60 was created by a committee composed of computing academics and like-minded people, while Fortran was dominated by the major computer company of the day, IBM (1963: list of 51 Fortran compilers; 1964: at least 43 Fortran compilers/versions), and COBOL was designed to be used by those strange business people (1963: list of 37 COBOL implementations/versions).
Design of the Whetstone benchmark
The Whetstone benchmark was once a widely cited measure of computer performance. This benchmark consisted of a single program, originally designed for Algol 60 based applications, and later translated to other languages (over 85% of published results used Fortran). The source used as representative of typical user programs came from scientific applications, which has some characteristics that are very non-representative of non-scientific applications, e.g., use of floating-point, and proportionally more multiplications and multidimensional array accesses. Dhrystone benchmark was later designed with the intent of being representative of a broader range of applications.
While rooting around for Whetstone result data, I discovered the book Algol 60 Compilation and Assessment by Brian Wichmann. Despite knowing Brian for 25 years and being very familiar with his work on compiler validation, I had never heard of this book (Knuth’s An Empirical Study of Fortran Programs has sucked up all the oxygen in this niche).
As expected, this 1973 book has a very 1960s model of cpu/compiler behavior, much the same as MIX, the idealised computer used by Knuth for the first 30-years of The Art of Computer Programming.
The Whetstone world view is of a WYSIWYG compiler (i.e., each source statement maps to the obvious machine code), and cpu instructions that always take the same number of clock cycles to execute (the cpu/memory performance ratio had not yet moved far from unity, for many machines).
Compiler optimization is all about trying not to generate code, and special casing to eke out many small savings; post-1970 compilers tried hard not to be WYSIWYG. Showing compiler correctness is much simplified by WYSIWIG code generation.
Today, there are application domains where the 1960s machine model still holds. Low power embedded systems may have cpu/memory performance ratios close to unity, and predictable instruction execution times (estimating worst-case execution time is a minor research field).
Creating a representative usage-based benchmark requires detailed runtime data on what the chosen representative programs are doing. Brian modified the Whetstone Algol interpreter to count how many times each virtual machine op-code was executed (see the report Some Statistics from ALGOL Programs for more information).
The modified Algol interpreter was installed on the KDF9 at the National Physical Laboratory and Oxford University, in the late 1960s. Data from 949 programs was collected; the average number of operations per program was 152,000.
The op-codes need to be mapped to Algol statements, to create a benchmark program whose compiled form executes the appropriate proportion of op-codes. Some op-code sequences map directly to statements, e.g., Ld addrof x, Ld value y, Store, maps to the statement: x:=y;.
Counts of occurrences of each language construct in the source of the representative programs provides lots of information about the proportions of the basic building blocks. It’s ‘just’ a matter of sorting out the loop counts.
For me, the most interesting part of the book is chapter 2, which attempts to measure the execution time of 40+ different statements running on 36 different machines. The timing model is 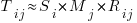 , where
, where 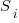 is the
is the 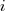 ‘th statement,
‘th statement, 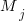 is the
is the 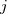 ‘th machine,
‘th machine, 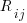 an adjustment factor intended to be as close to one as possible, and
an adjustment factor intended to be as close to one as possible, and 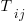 is execution time. The book lists some of the practical issues with this model, from the analysis of timing data from current machines, e.g., the impact of different compilers, and particular architecture features having a big performance impact on some kinds of statements.
is execution time. The book lists some of the practical issues with this model, from the analysis of timing data from current machines, e.g., the impact of different compilers, and particular architecture features having a big performance impact on some kinds of statements.
The table below shows statement execution time, in microseconds, for the corresponding computer and statement (* indicates an estimate; the book contains timings on 36 systems):
ATLAS MU5 1906A RRE Algol 68 B5500 Statement 6.0 0.52 1.4 14.0 12.1 x:=1.0 6.0 0.52 1.3 54.0 8.1 x:=1 6.0 0.52 1.4 *12.6 11.6 x:=y 9.0 0.62 2.0 23.0 18.8 x:=y + z 12.0 0.82 3.2 39.0 50.0 x:=y × z 18.0 2.02 7.2 71.0 32.5 x:=y/z 9.0 0.52 1.0 8.0 8.1 k:=1 18.0 0.52 0.9 121.0 25.0 k:=1.0 12.0 0.62 2.5 13.0 18.8 k:=l + m 15.0 1.07 4.9 75.0 35.0 k:=l × m 48.0 1.66 6.7 45.0 34.6 k:=l ÷ m 9.0 0.52 1.9 8.0 11.6 k:=l 6.0 0.72 3.1 44.0 11.8 x:=l 18.0 0.72 8.0 122.0 26.1 l:=y 39.0 0.82 20.3 180.0 46.6 x:=y ^ 2 48.0 1.12 23.0 213.0 85.0 x:=y ^ 3 120.0 10.60 55.0 978.0 1760.0 x:=y ^ z 21.0 0.72 1.8 22.0 24.0 e1[1]:=1 27.0 1.37 1.9 54.0 42.8 e1[1, 1]:=1 33.0 2.02 1.9 106.0 66.6 e1[1, 1, 1]:=1 15.0 0.72 2.4 22.0 23.5 l:=e1[1] 45.0 1.74 0.4 52.0 22.3 begin real a; end 96.0 2.14 80.0 242.0 2870.0 begin array a[1:1]; end 96.0 2.14 86.0 232.0 2870.0 begin array a[1:500]; end 156.0 2.96 106.0 352.0 8430.0 begin array a[1:1, 1:1]; end 216.0 3.46 124.0 452.0 13000.0 begin array a[1:1, 1:1, 1:1]; end 42.0 1.56 3.5 16.0 31.5 begin goto abcd; abcd : end 129.0 2.08 9.4 62.0 98.3 begin switch s:=q; goto s[1]; q : end 210.0 24.60 73.0 692.0 598.0 x:=sin(y) 222.0 25.00 73.0 462.0 758.0 x:=cos(y) 84.0 *0.58 17.3 22.0 14.0 x:=abs(y) 270.0 *10.20 71.0 562.0 740.0 x:=exp(y) 261.0 *7.30 24.7 462.0 808.0 x:=ln(y) 246.0 *6.77 73.0 432.0 605.0 x:=sqrt(y) 272.0 *12.90 91.0 622.0 841.0 x:=arctan(y) 99.0 *1.38 18.7 72.0 37.5 x:=sign(y) 99.0 *2.70 24.7 152.0 41.1 x:=entier(y) 54.0 2.18 43.0 72.0 31.0 p0 69.0 *6.61 57.0 92.0 39.0 p1(x) 75.0 *8.28 65.0 132.0 45.0 p2(x, y) 93.0 *9.75 71.0 162.0 53.0 p2(x, y, z) 57.0 *0.92 8.6 17.0 38.5 loop time |
The performance studies found wide disparities between expected and observed timings. Chapter 9 does a deep dive on six Algol compilers.
A lot of work and idealism went into gather the data for this book (36 systems!). Unfortunately, the computer performance model was already noticeably inaccurate, and advances in compiler optimization and cpu design meant that the accuracy was only going to get worse. Anyways, there is lots of interesting performance data on 1960 era computers.
Whetstone lived on into the 1990s, when the SPEC benchmark started to its rise to benchmark dominance.
Happy 60th birthday: Algol 60
Report on the Algorithmic Language ALGOL 60 is the title of a 16-page paper appearing in the May 1960 issue of the Communication of the ACM. Probably one of the most influential programming languages, and a language that readers may never have heard of.
During the 1960s there were three well known, widely used, programming languages: Algol 60, Cobol, and Fortran.
When somebody created a new programming languages Algol 60 tended to be their role-model. A few of the authors of the Algol 60 report cited beauty as one of their aims, a romantic notion that captured some users imaginations. Also, the language was full of quirky, out-there, features; plenty of scope for pin-head discussions.
Cobol appears visually clunky, is used by business people and focuses on data formatting (a deadly dull, but very important issue).
Fortran spent 20 years catching up with features supported by Algol 60.
Cobol and Fortran are still with us because they never had any serious competition within their target markets.
Algol 60 had lots of competition and its successor language, Algol 68, was groundbreaking within its academic niche, i.e., not in a developer useful way.
Language family trees ought to have Algol 60 at, or close to their root. But the Algol 60 descendants have been so successful, that the creators of these family trees have rarely heard of it.
In the US the ‘military’ language was Jovial, and in the UK it was Coral 66, both derived from Algol 60 (Coral 66 was the first language I used in industry after graduating). I used to hear people saying that Jovial was derived from Fortran; another example of people citing the language the popular language know.
Algol compiler implementers documented their techniques (probably because they were often academics); ALGOL 60 Implementation is a real gem of a book, and still worth a read today (as an introduction to compiling).
Algol 60 was ahead of its time in supporting undefined behaviors 😉 Such as: “The effect, of a go to statement, outside a for statement, which refers to a label within the for statement, is undefined.”
One feature of Algol 60 rarely adopted by other languages is its parameter passing mechanism, call-by-name (now that lambda expressions are starting to appear in widely used languages, call-by-name has a kind-of comeback). Call-by-name essentially has the same effect as textual substitution. Given the following procedure (it’s not a function because it does not return a value):
procedure swap (a, b); integer a, b, temp; begin temp := a; a := b; b:= temp end; |
the effect of the call: swap(i, x[i]) is:
temp := i; i := x[i]; x[i] := temp |
which might come as a surprise to some.
Needless to say, programmers came up with ‘clever’ ways of exploiting this behavior; the most famous being Jensen’s device.
The follow example of go to usage appears in: International Standard 1538 Programming languages – ALGOL 60 (the first and only edition appeared in 1984, after most people had stopped using the language):
go to if Ab < c then L17 else g[if w < 0 then 2 else n] |
Orthogonality of language use won out over the goto FUD.
The Software Preservation Group is a great resource for Algol 60 books and papers.
ALGEC: ALGorithmic language for EConomic problems
I have been reading about ALGEC, the computer language invented in the Soviet Union during the early 1960s, courtesy of a translation of the article Report on the Working Sessions of the Group on Algorithmic Languages for Processing Economic Information (GAIAPEI) by Rand.
The Soviet Union ran a command economy and the job of computers was obviously to process economic information.
The language is based on Algol 60, the default base language for the design of most establishment driven programming languages.
Since the Soviets were the only country to build a computer that used ternary logic, I was hoping that the language would include support for this ‘feature’. No such luck.
Two features caught by attention:
- Keywords can be written in a form that denotes their gender and number. For instance,
Booleancan be written:логическое(neuter),логический(masculine),логическая(feminine) andлогические(plural). - The keyword for the go to token is
to. There is obviously something about the use of Russian that makes it obvious that the word go should not be part of this keyword.
Do readers know of any other computer language which have been influence by features of the designers native human language (apart, obviously from all the English derived computer languages)?
Recent Comments