Type compatibility: name vs structural equivalence
What are the rules for deciding when two types are the same, or compatibility?
This question needs to be answered to decide whether an object of type T1 can be assigned to an object of type T2, whether they can be compared, added together, etc.
A wide collection of rules have been combined together, by various languages, for type compatibility of scalar types (e.g., integer, character, etc), but for aggregate types two rules dominate: name equivalence, and structural equivalence, or some combination.
With name equivalence, two types are the same if they are declared using the same name (e.g., the name of the tag for a union type, in C)
With structural equivalence, two types are compatible if they have a compatible structure, i.e., their internal contents are type compatible (this requires walking over each field/member checking that it is compatible). For instance, an object declared to have an aggregate type containing three integers is compatible with another aggregate type containing three integers (assuming any type modifiers, such as const’ness or mutability, are the same).
Structural compatibility becomes interesting when pointer types are involved; the pointed to types need to be checked and loops can occur, e.g., type S1 contains a field that has a type pointer to S2, which contains a field that has type pointer to S1.
While most types are easily checked for structural compatibility, every now and again aggregate types connect together in a way that makes it non-trivial to figure out which types are structurally compatible (dot file; needs graphviz):
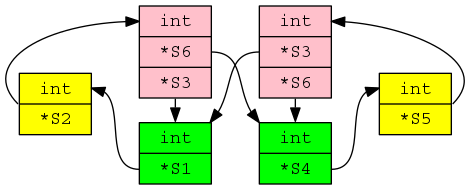
Handling the edge cases requires maintaining a stack of information about which pairs of types are currently being compared.
In C, type compatibility is a combination of name equivalence (for aggregate types in the same translation unit) and structural equivalence (for function types and aggregate types across translation units).
Function types have to use structural equivalence because the type in a function definition is anonymous (the function name that appears in the definition has this anonymous type), there is no name to compare.
Cycles cannot appear in function types (in C), because the identifier being defined in a typedef is not in scope until just after the completion of its declarator. It is not possible to refer to the identifier being defined insider its own definition (e.g., it is not possible to define a function that takes its own type as a parameter; in typedef int (*f)(f); the second f is a redundant parameter name, the scope of the type denoted by the first f begins just before the semicolon).
Structural equivalence across translation units is a hangover from the early days of C, when developers were sloppy when using (or not) tag names (with different people having different rules for using upper/lower case tag names); developers’ knew what the layout in memory was and created the necessary types for their use of this data.
Type compatibility via name equivalence is easy to explain and makes it explicit when developers are bending the rules (i.e., pointer to struct casts appear in the code).
Type compatibility via structural equivalence is the wild west, which still exists in some development environments.
Replication: not always worth the effort
Replication is the means by which mistakes get corrected in science. A researcher does an experiment and gets a particular result, but unknown to them one or more unmeasured factors (or just chance) had a significant impact. Another researcher does the same experiment and fails to get the same results, and eventually many experiments later people have figured out what is going on and what the actual answer is.
In practice replication has become a low status activity, journals want to publish papers containing new results, not papers backing up or refuting the results of previously published papers. The dearth of replication has led to questions being raised about large swathes of published results. Most journals only published papers that contain positive results, i.e., something was shown to some level of statistical significance; only publishing positive results produces publication bias (there have been calls for journals that publishes negative results).
Sometimes, repeating an experiment does not seem worth the effort. One such example is: An Explicit Strategy to Scaffold Novice Program Tracing. It looks like the authors ran a proper experiment and did everything they are supposed to do; but, I think the reason that got a positive result was luck.
The experiment involved 24 subjects and these were randomly assigned to one of two groups. Looking at the results (figures 4 and 5), it appears that two of the subjects had much lower ability that the other subjects (the authors did discuss the performance of these two subjects). Both of these subjects were assigned to the control group (there is a 25% chance of this happening, but nobody knew what the situation was until the experiment was run), pulling down the average of the control, making the other (strategy) group appear to show an improvement (i.e., the teaching strategy improved student performance).
Had one, or both, low performers been assigned to the other (strategy) group, no experimental effect would have shown up in the results, significantly reducing the probability that the paper would have been accepted for publication.
Why did the authors submit the paper for publication? Well, academic performance is based on papers published (quality of journal they appear in, number of citations, etc), a positive result is reason enough to submit for publication. The researchers did what they have been incentivized to do.
I hope the authors of the paper continue with their experiments. Life is full of chance effects and the only way to get a solid result is to keep on trying.
A Python Data Science hackathon
I was at the Man AHL Hackathon this weekend. The theme was improving the Python Data Science ecosystem. Around 15, or so, project titles had been distributed around the tables in the Man AHL cafeteria and the lead person for each project gave a brief presentation. Stable laws in SciPy sounded interesting to me and their room location included comfy seating (avoiding a numb bum is an underappreciated aspect of choosing a hackathon team, and wooden bench seating is not numbing after a while).
Team Stable laws consisted of Andrea, Rishabh, Toby and yours truly. Our aim was to implement the Stable distribution as a Python module, to be included in the next release of SciPy (the availability had been announced a while back and there has been one attempt at an implementation {which seems to contain a few mistakes}).
We were well-fed and watered by Man AHL, including fancy cream buns and late night sushi.
A probability distribution is stable if the result of linear combinations of the distribution has the same distribution; the Gaussian, or Normal, distribution is the most well-known stable distribution and the central limit theorem leads many to think, that is that.
Two other, named, stable distributions are the Cauchy distribution and most interestingly (from my perspective this weekend) the Lévy distribution. Both distributions have very fat tails; the mean and variance of the Cauchy distribution is undefined (i.e., the values jump around as the sample size increases, never converging to a fixed value), while they are both infinite for the Lévy distribution.
Analytic expressions exist for various characteristics of the Stable distribution (e.g., probability distribution function), with the Gaussian, Cauchy and Lévy distributions as special cases. While solutions for implementing these expressions have been proposed, care is required; the expressions are ill-behaved in different ways over some intervals of their parameter values.
Andrea has spent several years studying the Stable distribution analytically and was keen to create an implementation. My approach for complicated stuff is to find an existing implementation and adopt it. While everybody else worked their way through the copious papers that Andrea had brought along, I searched for existing implementations.
I found several implementations, but they all suffered from using approaches that delivered discontinuities and poor accuracies over some range of parameter values.
Eventually I got lucky and found a paper by Royuela-del-Val, Simmross-Wattenberg and Alberola-López, which described their implementation in C: Libstable (licensed under the GPL, perfect for SciPy); they also provided lots of replication material from their evaluation. An R package was available, but no Python support.
No other implementations were found. Team Stable laws decided to create a new implementation in Python and to create a Python module to interface to the C code in libstable (the bit I got to do). Two implementations would allow performance and accuracy to be compared (accuracy checks really need three implementations to get some idea of which might be incorrect, when output differs).
One small fix was needed to build libstable under OS X (change Makefile to link against .so library, rather than .a) and a different fix was needed to install the R package under OS X (R patch; Windows and generic Unix were fine).
Python’s ctypes module looked after loading the C shared library I built, along with converting the NumPy arrays. My PyStable module will not win any Python beauty contest, it is a means of supporting the comparison of multiple implementations.
Some progress was made towards creating a new implementation, more than 24 hours is obviously needed (libstable contains over 4,000 lines of code). I had my own problems with an exception being raised in calls to stable_pdf; libstable used the GNU Scientific Library and I tracked the problem down to a call into GSL, but did not get any further.
We all worked overnight, my first 24-hour hack in a very long time (I got about 4-hours sleep).
After Sunday lunch around 10 teams presented and after a quick deliberation, Team Stable laws were announced as the winners; yea!
Hopefully, over the coming weeks a usable implementation will come into being.
Influential philosophers of source code
Who is the most important/influential philosopher of source code? Source code, as far as I know, is not a subject that philosophers claim to be studying; but, the study of logic, language and the mind is the study of source code.
For many, Ludwig Wittgenstein would probably be the philosopher that springs to mind. Wittgenstein became famous as the world’s first Perl programmer, with statements such as: “If a lion could talk, we could not understand him.” and “Whereof one cannot speak, thereof one must be silent.”
Noam Chomsky, a linguist, might be another choice, based on his specification of the Chomsky hierarchy (which neatly categorizes grammars). But generative grammars (for which he is famous in linguistics) is about generating language, not understanding what has been said/written.
My choice for the most important/influential philosopher of source code is Paul Grice. A name, I suspect, that is new to most readers. The book to quote (and to read if you enjoy the kind of books philosophers write) is “Studies in the Way of Words”.
Grice’s maxims, provide a powerful model for human communication; the tldr:
- Maxim of quality: Try to make your contribution one that is true.
- Maxim of quantity: Make your contribution as informative as is required.
- Maxim of relation: Be relevant.
But source code is about human/computer communication, you say. Yes, but so many developers seem to behave as-if they were involved in human/human communication.
Source code rarely expresses what the developer means; source code is evidence of what the developer means.
The source code chapter of my empirical software engineering book is Gricean, with a Relevance theory accent.
More easily digestible books on Grice’s work (for me at least) are: “Relevance: Communication and Cognition” by Sperber and Wilson, and the more recent “Meaning and Relevance” by Wilson and Sperber.
The C++ committee has taken off its ball and chain
A step change in the approach to updates and additions to the C++ Standard occurred at the recent WG21 meeting, or rather a change that has been kind of going on for a few meetings has been documented and discussed. Two bullet points at the start of “C++ Stability, Velocity, and Deployment Plans [R2]”, grab reader’s attention:
● Is C++ a language of exciting new features?
● Is C++ a language known for great stability over a long period?
followed by the proposal (which was agreed at the meeting): “The Committee should be willing to consider the design / quality of proposals even if they may cause a change in behavior or failure to compile for existing code.”
We have had 30 years of C++/C compatibility (ok, there have been some nibbling around the edges over the last 15 years). A remarkable achievement, thanks to Bjarne Stroustrup over 30+ years and 64 full-week standards’ meetings (also, Tom Plum and Bill Plauger were engaged in shuttle diplomacy between WG14 and WG21).
The C/C++ superset/different issue has a long history.
In the late 1980s SC22 (the top-level ISO committee for programming languages) asked WG14 (the C committee) whether a standard should be created for C++, and if so did WG14 want to create it. WG14 considered the matter at its April 1989 meeting, and replied that in its view a standard for C++ was worth considering, but that the C committee were not the people to do it.
In 1990, SC22 started a study group to look into whether a working group for C++ should be created and in the U.S. X3 (the ANSI committee responsible for Information processing systems) set up X3J16. The showdown meeting of what would become WG21, was held in London, March 1992 (the only ISO C++ meeting I have attended).
The X3J16 people were in London for the ISO meeting, which was heated at times. The two public positions were: 1) work should start on a standard for C++, 2) C++ was not yet mature enough for work to start on a standard.
The, not so public, reason given for wanting to start work on a standard was to stop, or at least slow down, changes to the language. New releases, rumored and/or actual, of Cfront were frequent (in a pre-Internet time sense). Writing large applications in a version of C++ that was replaced with something sightly different six months later had developers in large companies pulling their hair out.
You might have thought that compiler vendors would be happy for the language to be changing on a regular basis; changes provide an incentive for users to pay for compiler upgrades. In practice the changes were so significant that major rework was needed by somebody who knew what they were doing, i.e., expensive people had to be paid; vendors were more used to putting effort into marketing minor updates. It was claimed that implementing a C++ compiler required seven times the effort of implementing a C compiler. I have no idea how true this claim might have been (it might have been one vendor’s approximate experience). In the 1980s everybody and his dog had their own C compiler and most of those who had tried, had run into a brick wall trying to implement a C++ compiler.
The stop/slow down changing C++ vs. let C++ “fulfill its destiny” (a rallying call from the AT&T rep, which the whole room cheered) finally got voted on; the study group became a WG (I cannot tell you the numbers; the meeting minutes are not online and I cannot find a paper copy {we had those until the mid/late-90s}).
The creation of WG21 did not have the intended effect (slowing down changes to the language); Stroustrup joined the committee and C++ evolution continued apace. However, from the developers’ perspective language change did slow down; Cfront changes stopped because its code was collapsing under its own evolutionary weight and usable C++ compilers became available from other vendors (in the early days, Zortech C++ was a major boost to the spread of usage).
The last WG21 meeting had 140 people on the attendance list; they were not all bored consultants looking for a creative outlet (i.e., exciting new features), but I’m sure many would be happy to drop the ball-and-chain (otherwise known as C compatibility).
I think there will be lots of proposals that will break C compatibility in one way or another and some will make it into a published standard. The claim will be that the changes will make life easier for future C++ developers (a claim made by proponents of every language, for which there is zero empirical evidence). The only way of finding out whether a change has long term benefit is to wait a long time and see what happens.
The interesting question is how C++ compiler vendors will react to breaking changes in the language standard. There are not many production compilers out there these days, i.e., not a lot of competition. What incentive does a compiler vendor have to release a version of their compiler that will likely break existing code? Compiler validation, against a standard, is now history.
If WG21 make too many breaking changes, they could find C++ vendors ignoring them and developers asking whether the ISO C++ standards’ committee is past its sell by date.
GDPR has a huge impact on empirical software engineering research
The EU’s General Data Protection Regulation (GDPR) is going to have a huge impact on empirical software engineering research. After 25 May 2018, analyzing source code will never be the same again.
I am not a lawyer and nothing qualifies me to talk about the GDPR.
People put their name in source code, bug tracking databases and discussion forums; this is personal identifying information.
Researchers use personal names to obtain information about a wide variety of activities, e.g., how much code did individuals write, how many bug reports did they process, contributions in discussions of one sort or another.
Open source licenses give others all kinds of rights (e.g., ability to use and modify source code), but they do not contain any provisions for processing personal data.
Adding a “I hereby give permission for anybody to process information about my name in any way they see fit.” clause to licenses is not going to help.
The GDPR requires (article 5: Principles relating to processing of personal data):
“Personal data shall be: … collected for specified, explicit and legitimate purposes and not further processed in a manner that is incompatible with those purposes;”
That is, personal data can only be processed for the specific reason it was collected, i.e., if you come up with another bright idea for analysis of data that has just been collected, it may be necessary to obtain consent, from those whose personal data it is, before trying out the bright idea.
It is not possible to obtain blanket permission (article 6, Lawfulness of processing):
“…the data subject has given consent to the processing of his or her personal data for one or more specific purposes;”, i.e., consent has to be obtained from the data subject for each specific purpose.
Github’s Global Privacy Practices shows that Github are intent on meeting the GDPR requirements, they include: “GitHub provides clear methods of unambiguous, informed consent at the time of data collection, when we do collect your personal data.”. Processing personal information, about an EU citizen, contained in source code appears to be a violation of Github’s terms of service.
The GDPR has many other requirements, e.g., right to obtain information on what information is held and right to be forgotten. But, the upfront killer is not being able to cheaply collect lots of code and then use personal information to help with the analysis.
There are exceptions for: Processing for archiving, scientific or historical research or statistical purposes. Can somebody who blogs and is writing a book claim to be doing scientific research? People who know more about these exceptions than me, tell me that there could be a fair amount of paperwork involved when making use of the exception, i.e., being able to show that privacy safeguards are in place.
Then, there is the issue of what constitutes personal information. Git’s hashing algorithm makes use of the committer’s name and/or email address. Is a git hash personal identifying information?
A good introduction to the GDPR for developers, and one for researchers.
Reliability chapter added to “Empirical software engineering using R”
The Reliability chapter of my Empirical software engineering book has been added to the draft pdf (download here).
I have been working on this draft for four months and it still needs lots of work; time to move on and let it stew for a while. Part of the problem is lack of public data; cost and schedule overruns can be rather public (projects chapter), but reliability problems are easier to keep quiet.
Originally there was a chapter covering reliability and another one covering faults. As time passed, these merged into one. The material kept evaporating in front of my eyes (around a third of the initial draft, collected over the years, was deleted); I have already written about why most fault prediction research is a waste of time. If it had not been for Rome I would not have had much to write about.
Perhaps what will jump out at people most, is that I distinguish between mistakes in code and what I call a fault experience. A fault_experience=mistake_in_code + particular_input. Most fault researchers have been completely ignoring half of what goes into every fault experience, the input profile (if the user does not notice a fault, I do not consider it experienced) . It’s incredibly difficult to figure out anything about the input profile, so it has been quietly ignored (one of the reasons why research papers on reported faults are such a waste of time).
I’m also missing an ‘interesting’ figure on the opening page of the chapter. Suggestions welcome.
I have not said much about source code characteristics. There is a chapter covering source code, perhaps some of this material will migrate to reliability.
All sorts of interesting bits and pieces have been added to earlier chapters. Ecosystems keeps growing and in years to come somebody will write a multi-volume tomb on software ecosystems.
I have been promised all sorts of data. Hopefully some of it will arrive.
As always, if you know of any interesting software engineering data, please tell me.
Source code chapter next.
McCabe’s cyclomatic complexity and accounting fraud
The paper in which McCabe proposed what has become known as McCabe’s cyclomatic complexity did not contain any references to source code measurements, it was a pure ego and bluster paper.
Fast forward 10 years and cyclomatic complexity, complexity metric, McCabe’s complexity…permutations of the three words+metrics… has become one of the two major magical omens of code quality/safety/reliability (Halstead’s is the other).
It’s not hard to show that McCabe’s complexity is a rather weak measure of program complexity (it’s about as useful as counting lines of code).
Just as it is possible to reduce the number of lines of code in a function (by putting all the code on one line), it’s possible to restructure existing code to reduce the value of McCabe’s complexity (which is measured for individual functions).
The value of McCabe’s complexity for the following function is 5 16, i.e., and there are 16 possible paths through the function:
int main(void) { if (W) a(); else b(); if (X) c(); else d(); if (Y) e(); else f(); if (Z) g(); else h(); } |
each if…else contains two paths and there are four in series, giving 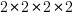 paths.
paths.
Restructuring the code, as below, removes the multiplication of paths caused by the sequence of if…else:
void a_b(void) {if (W) a(); else b();} void c_d(void) {if (X) c(); else d();} void e_f(void) {if (Y) e(); else f();} void g_h(void) {if (Z) g(); else h();} int main(void) { a_b(); c_d(); e_f(); g_h(); } |
reducing main‘s McCabe complexity to 1 and the four new functions each have a McCabe complexity of two.
Where has the ‘missing’ complexity gone? It now ‘exists’ in the relationship between the functions, a relationship that is not included in the McCabe complexity calculation.
The number of paths that can be traversed, by a call to main, has not changed (but the McCabe method for counting them now produces a different answer)
Various recommended practice documents suggest McCabe’s complexity as one of the metrics to consider (but don’t suggest any upper limit), while others go as far as to claim that it’s bad practice for functions to have a McCabe’s complexity above some value (e.g., 10) or that “Cyclomatic complexity may be considered a broad measure of soundness and confidence for a program“.
Consultants in the code quality/safety/security business need something to complain about, that is not too hard or expensive for the client to fix.
If a consultant suggested that you reduced the number of lines in a function by joining existing lines, to bring the count under some recommended limit, would you take them seriously?
What about, if a consultant highlighted a function that had an allegedly high McCabe’s complexity? Should what they say be taken seriously, or are they essentially encouraging developers to commit the software equivalent of accounting fraud?
Top, must-read paper on software fault analysis
What is the top, must read, paper on software fault analysis?
Software Reliability: Repetitive Run Experimentation and Modeling by Phyllis Nagel and James Skrivan is my choice (it’s actually a report, rather than a paper). Not only is this report full of interesting ideas and data, but it has multiple replications. Replication of experiments in software engineering is very rare; this work was replicated by the original authors, plus Scholz, and then replicated by Janet Dunham and John Pierce, and then again by Dunham and Lauterbach!
I suspect that most readers have never heard of this work, or of Phyllis Nagel or James Skrivan (I hadn’t until I read the report). Being published is rarely enough for work to become well-known, the authors need to proactively advertise the work. Nagel, Dunham & co worked in industry and so did not have any students to promote their work and did not spend time on the academic seminar circuit. Given enough effort it’s possible for even minor work to become widely known.
The study run by Nagel and Skrivan first had three experienced developers independently implement the same specification. Each of these three implementations was then tested, multiple times. The iteration sequence was: 1) run program until fault experienced, 2) fix fault, 3) if less than five faults experienced, goto step (1). The measurements recorded were fault identity and the number of inputs processed before the fault was experienced.
This process was repeated 50 times, always starting with the original (uncorrected) implementation; the replications varied this, along with the number of inputs used.
For a fault to be experienced, there has to be a mistake in the code and the ‘right’ input values have to be processed.
How many input values need to be processed, on average, before a particular fault is experienced? Does the average number of inputs values needed for a fault experience vary between faults, and if so by how much?
The plot below (code+data) shows the numbers of inputs processed, by one of the implementations, before individual faults were experienced, over 50 runs (sorted by number of inputs):
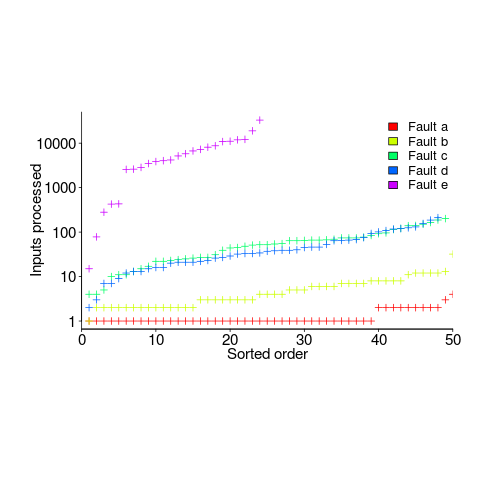
Different faults have different probabilities of being experienced, with fault a being experienced on almost any input and fault e occurring much less frequently (a pattern seen in the replications). There is an order of magnitude variation in the number of inputs processed before particular faults are experienced (this pattern is seen in the replications).
Faults were fixed as soon as they were experienced, so the technique for estimating the total number of distinct faults, discussed in a previous post, cannot be used.
A plot of number of faults found against number of inputs processed is another possibility. More on that another time.
Suggestions for top, must read, paper on software faults, welcome (be warned, I think that most published fault research is a waste of time).
Estimating the number of distinct faults in a program
In an earlier post I gave two reasons why most fault prediction research is a waste of time: 1) it ignores the usage (e.g., more heavily used software is likely to have more reported faults than rarely used software), and 2) the data in public bug repositories contains lots of noise (i.e., lots of cleaning needs to be done before any reliable analysis can done).
Around a year ago I found out about a third reason why most estimates of number of faults remaining are nonsense; not enough signal in the data. Date/time of first discovery of a distinct fault does not contain enough information to distinguish between possible exponential order models (technical details; practically all models are derived from the exponential family of probability distributions); controlling for usage and cleaning the data is not enough. Having spent a lot of time, over the years, collecting exactly this kind of information, I was very annoyed.
The information required, to have any chance of making a reliable prediction about the likely total number of distinct faults, is a count of all fault experiences, i.e., multiple instances of the same fault need to be recorded.
The correct techniques to use are based on work that dates back to Turing’s work breaking the Enigma codes; people have probably heard of Good-Turing smoothing, but the slightly later work of Good and Toulmin is applicable here. The person whose name appears on nearly all the major (and many minor) papers on population estimation theory (in ecology) is Anne Chao.
The Chao1 model (as it is generally known) is based on a count of the number of distinct faults that occur once and twice (the Chao2 model applies when presence/absence information is available from independent sites, e.g., individuals reporting problems during a code review). The estimated lower bound on the number of distinct items in a closed population is:
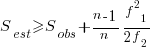
and its standard deviation is:
![S_{sd-est}={f_1}/{f_2}k sqrt{f_2(0.5/{k}+{f_1}/{f_2} [1+0.25 {f_1}/{f_2}])} S_{sd-est}={f_1}/{f_2}k sqrt{f_2(0.5/{k}+{f_1}/{f_2} [1+0.25 {f_1}/{f_2}])}](https://shape-of-code.com/wp-content/plugins/wpmathpub/phpmathpublisher/img/math_977.5_e69346120e72f31d04a47c9fcf64c4dd.png)
where: 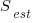 is the estimated number of distinct faults,
is the estimated number of distinct faults, 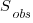 the observed number of distinct faults,
the observed number of distinct faults,  the total number of faults,
the total number of faults, 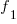 the number of distinct faults that occurred once,
the number of distinct faults that occurred once, 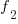 the number of distinct faults that occurred twice,
the number of distinct faults that occurred twice, 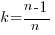 .
.
A later improved model, known as iChoa1, includes counts of distinct faults occurring three and four times.
Where can clean fault experience data, where the number of inputs have been controlled, be obtained? Fuzzing has become very popular during the last few years and many of the people doing this work have kept detailed data that is sometimes available for download (other times an email is required).
Kaminsky, Cecchetti and Eddington ran a very interesting fuzzing study, where they fuzzed three versions of Microsoft Office (plus various Open Source tools) and made their data available.
The faults of interest in this study were those that caused the program to crash. The plot below (code+data) shows the expected growth in the number of previously unseen faults in Microsoft Office 2003, 2007 and 2010, along with 95% confidence intervals; the x-axis is the number of faults experienced, the y-axis the number of distinct faults.
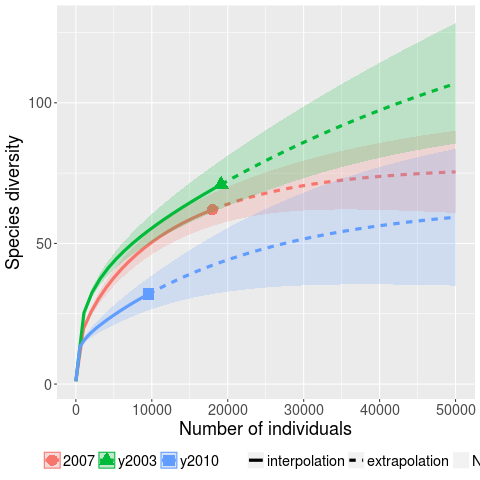
The take-away point: if you are analyzing reported faults, the information needed to build models is contained in the number of times each distinct fault occurred.
Recent Comments