Instructions that cpus don’t need to support
What instructions can computers do without (an earlier post covered instructions they should support)?
The R in RISC was supposed to stand for Reduced, but in practice almost all the instructions you would expect were supported. What was missing were the really complicated instructions that machines of the time (last 1980s), like the VAX, supported (analysis of instruction set usage showed that these complicated instructions were rarely used; from the compiler perspective the combination sequence of operations supported by these instructions rarely occurred in code).
One instruction that was often missing from the early RISC processors was integer multiply. Compilers were expected to generate a series of instructions that had the same effect. Some of the omitted ‘basic’ instructions got added to later versions of the processors that survived commercially (e.g., SPARC).
The status register is still a common omission from RISC designs (at least for the integer operations). Where is the data showing that in the grand scheme of things (i.e., processor performance running real programs), status registers slow things down? I know that hardware designers don’t like them because they introduce bottlenecks. I don’t recall ever having seen an analysis of instruction set usage targeted at the impact of status registers on generated code. Pointers welcome.
These days, nobody seems to analyze instruction set usage like they did in times past. Perhaps Intel’s marketing and the demise of almost every cpu vendor has dampened enthusiasm for researching new cpu designs. These days most new cpu designs seem to be fashion driven, rather than data driven.
Do computers need registers? An issue that once attracted lots of research was the optimal number of registers for a processor. The minimum number of registers (or temporary storage locations) needed to evaluate an expression was known by 1970. There were various studies of the impact, on code generation, of increasing/decreasing the number of registers available to the compiler. But these studies were done using 1990s era compilers and modern compilers do many more optimizations; whole program optimization ought to be able to make use of many more registers than are probably available on today’s processors (at least I think so, until somebody does a study that shows otherwise). There is a register-less processor that is supposed to be taking the world by storm, sometime soon.
Do computers need to support the IEEE floating-point representation? Logarithmic number systems are starting to be used in various devices, but accuracy remains an issue for some applications.
Software engineering is fertile ground for the belief in silver bullets
The idea that there exists some wonderful technique or methodology, which solves one or more perceived software engineering problems, was given a name in 1986; the title of Brooks’ paper No Silver Bullet is a big clue that the author does not think it exists. Indeed, over the years a steady stream of papers have attempted to dispel the idea that silver bullets exist. These attempts have two things in common: the use of reasoning and facts to make their case, and failure to dispel the idea that there are no silver bullets in software engineering.
Now, I am a great fan of reasoning using facts, but I am also a fan of evidence driven approaches to solving problems. There is now over 30 years of evidence that reasoning using facts is not an effective means of convincing people that silver bullets don’t exist.
Belief in silver bullets will not go away until it ceases to be in some peoples’ interest for them to exist.
If you have something to sell, there is a benefit to having customers believe in silver bullets: the product/research will dramatically improve performance, time to market, costs, profitability, etc…
Belief in silver bullets is not unfounded. Computing has a 70-year history of things going faster, getting cheaper and systems doing what was once thought impossible. The press has bought into this and amazing success stories abound. Having worked on a few projects that delivered faster/cheaper/impossible systems, I know that no silver bullets were involved, just lots of hard work and sometimes being in the right place at the right time. Hard work and happenstance don’t make for feel-good headlines, and rarely get mentioned in the press.
When faced with a problem, the young and inexperienced tend to be optimists; there must be a silver bullet better way of doing this that is fast/cheap/efficient. The computing field has been evolving so rapidly that many of those involved are young and inexperienced; fertile ground for belief in silver bullets to flourish.
Consequences of a belief in silver bullets in industry include, time/cost overruns on projects and money wasted on tools that are never used. In academia a belief in silver bullets results in the pointless invention of new programming languages, methodologies, programming techniques, etc.
The belief in silver bullets will not fade away until the rate of change in computing slows to a crawl and most of those involved have gained substantial experience from which they can see that results come from hard work (and some amount of luck).
Time taken to compile a source file
How long will it take to compile a source file?
When computers were a lot slower than they are today, this question was of general interest. Job scheduling is more effective when reliable runtime estimates are available, and developers want to know if there is enough time to get a coffee before the compile finishes.
An embarrassing fact about compile time performance, used to be that a large percentage of compile time was spent doing lexical analysis [“The cost of lexical analysis”, I cannot find an online copy]. Why was this embarrassing? Compiler writers like to boast about all the fancy optimizations their compiler does; but doing fancy stuff consumes lots of resources, so why were compilers spending so much of their time doing simple things like lexical analysis? The reality was that fancy compiler optimizations were not commercially viable until developer computers contained tens of megabytes of memory, i.e., very few pre-1990 compilers did any real optimization (people are still fussing over lexer performance).
An analysis of the data in Captain Dennis Miller’s Masters thesis (late Rome period), finds compile time is proportional to the square root of the number of tokens in the source (code+data); more complicated models are a slightly better fit. Where did square root come from? I expected a linear relationship, but would be willing to go with log. The measurements are from Ada compilers in the mid 1980s. I know several people who worked on Ada compilers during that time, and they were implementing the latest fancy optimizations (Ada was going to be the next big thing and the venture capital was flowing; big companies, with big computers were going to be paying lots of money to use Ada, but then microcomputers came along). I think that square root is driven by OS resource limitations, the compilers are using lots of memory and a noticeable amount of time is spent swapping.
So computers got a lot faster and people lost interest in estimates of how long it would take to compile individual files. I have not seen any interest in predicting how long it would take to compile whole projects (just complaints about how long it takes). There has been some work on progress indicators, updated as compilation progresses, which is a step in the right direction. Perhaps somebody has recorded compile time information and thrown machine learning at it; I usually ignore machine learning papers applied to software engineering and perhaps I have missed something. Pointers to project compile time prediction work welcome.
Then along came just-in-time compilation. Now people want to estimate how long it will take to generate machine code from some intermediate form, that is being interpreted.
The plot below (thanks to Rafael Auler for kindly supplying the data from his paper) shows the time taken to generate code from functions containing a given number of LLVM instructions (an intermediate code), at optimization level O3. The red line is a regression fit to one of the ‘arms’ and shows constant time for less than 100’ish instructions and then a linear relationship. I have no idea why the time is roughly constant for a large number of functions.
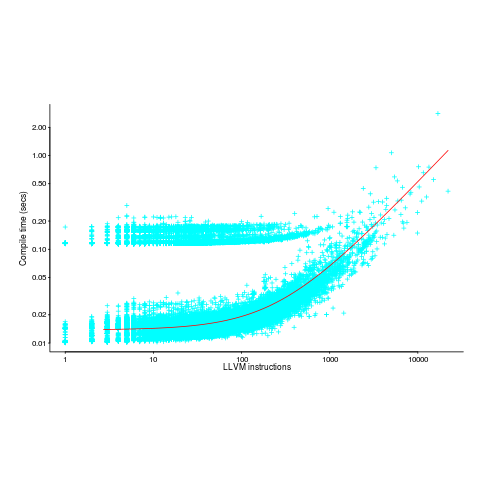
There is a lot of variation for function containing the same number of instructions. This is to be expected when lots of different optimizations are being tried; sometimes a function will contain lots of the kind of code that a particular optimization spends lot of times process and sometimes the code will not contain anything interesting (i.e., no optimizations are found).
Undergraduates and learning to program
I last looked at the research on teaching programming around 10 years ago and I have been catching up with what has been going on; in brief: same old, same old. One of the best papers on the subject is still: Language-independent conceptual “Bugs”
The research activity is still focused on making the tools and language ‘better’. There is a defining silence on the possibility that those doing the teaching could not teach their way out of a paper bag. Nobody is brave enough to suggest that teacher training might be a worthwhile investment, or that lectures oriented to what is useful (rather than what the lecturer finds interesting) would be appreciated by students.
I have always thought that researching the teaching of programming had no practical purpose, other than possibly helping universities increase the number of students graduating with computing degrees (some universities are solving the problem students have with programming by offering degrees that don’t involve being able to program). I still think that teaching programming to school children is at best a waste of time.
My experience with students learning to program is from a very long time ago. The process involved listening to confusing and disjoint lectures, reading books and figuring out what worked by trial and error. Students were not taught to program, they got thrown in at the deep and were expected to survive. Anybody who could handle this stood some chance of being able to handle developing software in the ‘real world’; universities were (accidentally) graduating people with the skills industry needed. However, these days universities are supposed to be customer focused, what industry needs is irrelevant (my experience of sitting on departmental industry panels is that the head of department tells us what they are thinking of doing {i.e., new courses for which there will be lots of paying students} and we try to talk him/her out of the sillier ideas); too many fee paying students find programming too hard, let’s offer computing degrees that don’t require any programming has been the only workable solution to-date.
Would you hire a recent graduate, for a development role, who had trouble figuring out how to fix syntax errors in their code? Surely, the minimum requirement is somebody who gets some pleasure from coding, even if they don’t want to spend lots of time doing it.
There is a shortage of software developers and flying turkeys are still with us.
Number of parameters vs. accessing globals
I spend a lot of time looking at software engineering data, asking, what is the story here?
In a previous post I suggested that the distribution of the number of functions defined to have a given number of parameters, might be a signature of developer beliefs about the relative cost of parameter passing vs accessing globals.
Looking at the data that Iran Rodrigues Gonzaga Junior made available (good man), as part of his thesis Empirical Studies on Fine-Grained Feature Dependencies, I saw it contained information about the number of parameters in a function definition and whether functions accessed a global (Gonzaga’s research question is in another direction; I am always repurposing data).
Are functions that access globals, defined with fewer parameters, compared to those that do not contain any such access? The plot below shows a count of the number of functions defined to have a given number of parameters, for four systems written in C; the solid lines are functions that did not access globals, the dashed lines are functions that accessed globals (code+data).
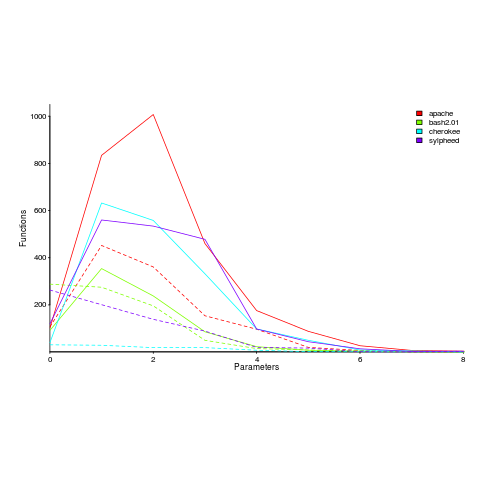
Over all 50 projects measured, functions that don’t access globals are defined, on average, to have an extra 0.7 parameters (the fitted Poisson regression models are better than a poke in the eye {i.e., the distribution is not really Poisson}, it’s more informative to look at the plotted data).
There is a lot of variation between projects (I picked these four because they were the larger projects and showed variation in behaviors). While the shape of the distributions varies a lot, there is always a noticeable difference in the mean.
Is this difference between projects a difference in developer beliefs, a difference in application requirements, a difference in developer coding habits (and parameter usage is a side effect; are there really that many getters and setters)?
I was hoping for a simple answer, and could not find one. Since I am writing a book and not researching individual issues in detail, it’s time to move on.
Ideas welcome.
Main memory: the crucial component that vendors don’t mention
CPU performance hogs the limelight when people discuss the year-on-year increases in computing power that used to occur.
This focus on cpu performance was/is driven by marketing, the people with the money either don’t want customers thinking about the performance impact of main memory size or speed, or want them to treat the processor as the most important component of a computer. Vendors want processor performance to drive customer purchase decisions.
Hardware manufacturers used to entice new customers with low cost machines, containing minimal memory. Once a customer started to use their shiny new computer, they found that it did save them lots of time and money, but also they needed more memory (which could only be brought from the manufacturer and was not cheap).
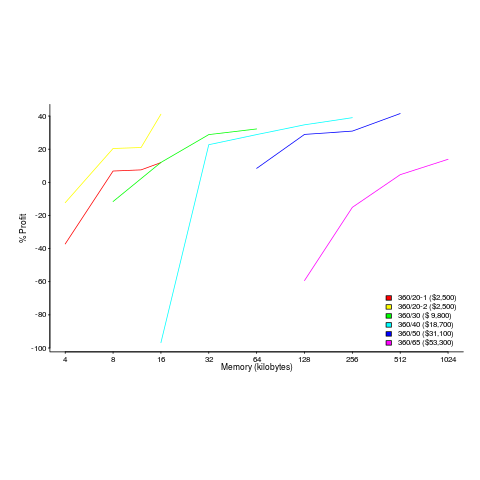
The plot below shows the prices IBM charged for System 360s, in 1966. Anti-trust investigations uncover all kinds of interesting data, like selling low-spec equipment at a loss to entice customers and make life difficult for competitors (code+data for all plots).
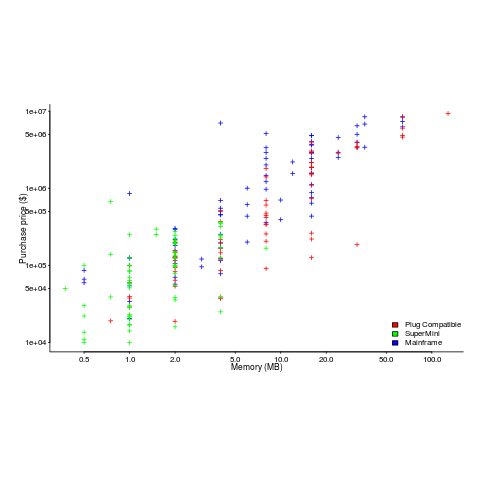
The plot below (data from the 19 Aug 1985 issue of ComputerWorld) shows how the price of computers increased as the minimum about of memory they supported increased.
Yes, in 1985 top end computers came with over 50M of memory; but most customers thought themselves lucky if they had a few megabytes.
If the processor is slow, it just takes longer for programs to run. If the computer does not have enough memory, programs cannot run. For most applications memory requirements are addressed first, followed by processor performance; memory requirements is the number one issue. The optimizations that commercial compilers could perform were limited by the memory capacity of developer machines.
Intel’s main line of business used to be selling memory chips, but these chips became commodity items as more companies entered the market; Intel bet the farm on selling processors and the rest is history. As a seller of a unique product it was/is in Intel’s interest to spend lots of money on marketing the benefits of processor performance; sellers of commodity items (such as memory chips) don’t have nearly as much to gain from generic product marketing, because customers may choose to buy from other sellers (in such markets sellers have to concentrate on marketing themselves).
Memory capacity/speed and cpu speed are two aspects of system performance; they need to be balanced to meet customer drive application requirements. The plot below shows the SPEC cpu integer performance of 4,332 systems running at various clock rates; the colors denote the different peak memory transfer rates of the memory chips in these systems (code+data).
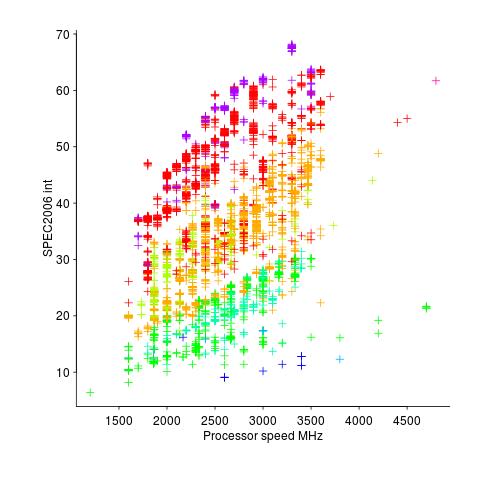
These days (and perhaps in the past, I don’t have any data), memory performance is a much better predictor of system performance, but vendors don’t have an incentive to market this fact.
EDG and Github are both logical purchases for Microsoft
It looks like my prediction that Microsoft buys Github may be about to come true.
Microsoft has been sluggish in integrating their LinkedIn purchase into their identity management system. Lots of sites have verify identity using Github options (or at least the kind of sites I visit do), so perhaps LinkedIn identity will be trialed via Github.
A Github purchase will also allow Microsoft to directly connect lots of developers to Azure. Being able to easily build and execute Github code on Azure is the bait, customer data is where the money is; making Github more data friendly is an obvious first priority for new owners.
Who else should Microsoft buy? As a protective move, I think they should snap up Edison Design Group (EDG) before somebody else does. Readers outside of the compiler/static analysis/C++ standards world are unlikely to have heard of EDG. They sell C/C++ front ends (plus other languages) that support all the historical features/warts supported by other C/C++ compilers. The features only found in Microsoft’s compilers is what make it very costly/time-consuming for many companies to port their applications to other platforms; developer use of Microsoft compiler dependent features is a moat that makes it difficult for many companies to leave the Microsoft ecosystem. EDG have been in the business a long time and have built up an extensive knowledge of vendor specific compiler features; the kind of knowledge that can only be obtained by having customers tell you what language constructs they are using that your current product does not handle (and what those constructs actually mean).
What would happen if a very large company bought EDG, and open sourced its code (to make it easier for Windows developers to switch platforms, not to make any money off compiler related tools)? Somebody would have to bolt on a back-end, to generate code; but that would not be hard (EDG have designed their product to make this easy). A freely available compiler, supporting all/most of the foibles of the Microsoft C++ compiler, would tempt many Windows only developers to give it a go. A free compiler removes management from the loop, developers can try things out as a side project, without having to get management approval to spend money on a compiler (from practical experience I know how hard it is to sell compatible compiler products, i.e., there is no real money to be made by anybody doing this commercially).
Is this risk, to Microsoft, really worth the (relatively) low cost of buying EDG? The EDG guys are not getting any younger, why wouldn’t they be willing sell?
The age of the Algorithm is long gone
I date the age of the Algorithm from roughly the 1960s to the late 1980s.
During the age of the Algorithms, developers spent a lot of time figuring out the best algorithm to use and writing code to implement algorithms.
Knuth’s The Art of Computer Programming (TAOCP) was the book that everybody consulted to find an algorithm to solve their current problem (wafer thin paper, containing tiny handwritten corrections and updates, was glued into the library copies of TAOCP held by my undergraduate university; updates to Knuth was news).
Two developments caused the decline of the age of the Algorithm (and the rise of the age of the Ecosystem and the age of the Platform; topics for future posts).
- The rise of Open Source (it was not called this for a while), meant it became less and less necessary to spend lots of time dealing with algorithms; an implementation of something that was good enough, was available. TAOCP is something that developers suggest other people read, while they search for a package that does something close enough to what they want.
- Software systems kept getting larger, driving down the percentage of time developers spent working on algorithms (the bulk of the code in commercially viable systems deals with error handling and the user interface). Algorithms are still essential (like the bolts holding a bridge together), but don’t take up a lot of developer time.
Algorithms are still being invented, and some developers spend most of their time working with algorithms, but peak Algorithm is long gone.
Perhaps academic researchers in software engineering would do more relevant work if they did not spend so much time studying algorithms. But, as several researchers have told me, algorithms is what people in their own and other departments think computing related research is all about. They remain shackled to the past.
Premium mediocrity is software engineering’s demographic
Software engineering is one of the skills needed to write software, but outside of student coursework is rarely an end in itself. Software is written to do something and the person writing the code needs to know about the something.
If enough people are involved in something, a job title gets created by inserting the appropriate application domain name before ‘software engineer’, e.g., the something software engineer; systems software engineering was one of the first recorded uses of ‘software engineering’, ’embedded software engineer’ is a common usage and more recently ‘research software engineer’ has been trending.
Customers want the software systems they use to fulfill their needs. Implementing a software system involves figuring out what the needs are, how best to implement them using the available resources and producing usable software; all within a given amount of time and money.
How much software engineering knowledge and skill does a something software engineer need? The obvious answer is: enough to get the something done. Ok, how much is needed to get the something done?
There are so many hours in a day: what percentage of available time is best spent learning about software engineering, what percentage leaning about the something and what percentage doing rather than learning?
The only data I have for answering this question is my own experience of talking to people, from a wide range of business and application areas, whose job includes writing software. My background is compilers (from C to Cobol) and static analysis, my knowledge of end-user application domains is derived from talking to the developers who were using the compilers or static analysis tools I was working on at the time.
I have always been struck by the minimalist knowledge of most developers, when it comes to the programming language they were using. It took a while, but eventually I accepted the obvious: most developers don’t need to know much about the language they are using to get their job done.
By a process that resembles incentivized trial and error, people learn how to write code that does what they want; the compiler does not complain and the output looks ok. For some languages, I used to be able to work out which books a relatively new developer had used to guide their learning, by matching a book’s example code snippets with the code they had written.
This minimalist knowledge approach to programming languages is cost effective because most code is simple and has a short lifetime; the cost of learning lots of language details does not provide enough benefit to be worthwhile.
I am a minimalist language Python developer. Why would I spend time learning more about the semantics of Python than I need to?
What are the benefits of being a language expert? Compiler writers get paid to learn the ins and outs of a language and I know a few people who became language experts without being compiler writers (they got hooked on knowing the language). I have found it useful for keeping my code simple (I am not tempted to write complicate code, or use obscure constructs, in the mistaken belief that they are better than the simple stuff), it is also useful for figuring out other people’s complicated or obscure usage (created intentionally or accidentally).
These benefits are not enough to convince me to learn more about Python, the language. I am content to wait until I need to learn more.
I have occasionally taught advanced programming courses, aimed at developers with a few years experience working in industry. These courses had to include the word ‘advanced’ in their title, otherwise developers with a few years experience would never have signed-up; ‘advanced’ is a necessary marketing signal (others who have run such courses report the same behavior). The course contents were essentially a review of basic material, with lots of examples; most of those attending did not know enough to follow real advanced material. The courses were really about uncovering and correcting bad habits that attendees had picked up over time (often, a technique was discovered to fix a problem and then subsequently adopted for more general use).
What about general software engineering skills? A minimalist knowledge approach to software engineering is cost effective because most code does not exist long enough to make it worthwhile investing in reducing future maintenance costs. Yes, it is more expensive for those that survive to become commonly used, but think of all the savings from not investing in those that did not survive. Software engineering decisions should not be driven by surviorship bias.
The first requirement of any commercial software system is to attract paying customers. In a rapidly changing market, being first with a saleable product can be the difference between life and death. Minimizing software engineering effort saves time and money (in the short term). If the product is a success, there will be money to pay for what needs to be done, if the product fails nobody cares. I have seen a lot of software systems that are a commercial success and a complete software engineering mess; successful, well engineered software is less common (or perhaps they just don’t need me to help them out).
Software engineering mediocrity is not only viable, for most people it’s the outcome of making a cost/benefit decision to invest their learning time in the application domain, not software engineering (or computer language).
Of course, nobody wants to be seen as being mediocre (for some people, mediocre overstates their skill level); their behavior is premium mediocre.
There are a few application areas where software engineering skills are needed, e.g., safety critical software and warehouse scale computing. A few high profile cases are hiding the reality that whatever works is cost effective for most software solutions.
Replicating results using research software
The reproducibility of results, from scientific studies, has always been an important issue. Over the last few years software has become a hot topic in reproducibility circles; many researchers have an expectation that if they run the original researcher’s software, they will replicate the results. Reality has not lived up to their expectations and there has been a lot of flapping around looking for a solution. There is a solution, but first, why does the problem exist?
I have spent a lot of time porting software to different compilers (when I was in the compiler business, I wanted everybody to port their applications to the compiler I was working), different hardware (oh, the days when every major vendor had at least one distinct cpu; not like today where it’s x86, ARM, or embedded), different operating systems (umpteen flavors of Unix, all with slightly different header file contents and library behavior; the Unix wars were good for those in the porting business) and every now and again different languages (by translating).
The Wintel alliance wiped out variation in cpus and operating systems (they can still be found lurking in dark corners) and open source compilers created a near monoculture of compilers for the major languages.
The major software portability problems of 30 years ago have become rather minor. But software portability problems that once tended to be minor (at least for scientific software), have grown to become a major headache. Today’s major portability problems center around evolution of the libraries/packages being used, and longer term the evolution of the language(s) used.
Evolution has created development ecosystems where there are rampant dependencies on specific, or earlier than, or later than versions of libraries/packages. I have been out of the porting business for several decades, but talking to those doing it today, the story is the same; experience in porting from A to B is everything, second best is talking to somebody else who has gone in that direction and third best are the one-line forums such as stackoverflow.
Researchers are doing research on who-knows-what and probably have need-to-know knowledge of software and the libraries they are using, the researchers receiving a copy of the original software might know less. What is the probability that the originating and receiving researchers have exactly the same versions of libraries installed? The receiving researcher may not have any of the required libraries installed, and promptly install the latest version (which may well be more recent than the ones used by the original researcher).
A solution is available; distribute a duplicate of the researchers complete system as a container, e.g., a Docker image.
Containers solve the replication problem. But these days people want more, they actually think it should be possible to take research software and modify it to suite their own needs. Good luck with that.
Research software is written to solve a problem, often by people writing their first non-trivial programs (i.e., they are novices), with no incentive to produce something that is easy for others to use. When software is written by experienced developers, who have an incentive to build something that is easy for others to work with, multiple reimplementations are often still required to achieve something of decent quality. Creating robust software, that others can use, is very hard.
The problem with software is its invisibility; the difficulties are not visible. When the internal operations are visible, the difficulties of making changes are easier to see.
James Albert Bonsack’s cigarette rolling machine (from Wikipedia).
Recent Comments