Enthusiasm on the Fortran standards committee
The Fortran language standards committee, SC22/WG5, has an unusual situation on its hands. Two people have put themselves forward to chair the committee, when the current chairman’s three year term ends. What is unusual is that it is often difficult to find anybody willing to do the job.
The two candidates are the outgoing chair (the person who invariably does the job, until they decide they have had enough, or can arm wrestle someone else to do it), and a scientist at Los Alamos; I don’t know either person.
SC22 (the ISO committee responsible for language standards), and INCITS (the US Standards body; the US is the Fortran committee secretariate) will work something out.
I had heard that the new guy was ruffling some feathers, and I thought good for him (committees could do with having their feathers ruffled every now and again). Then I read the running for convenor announcement; oh dear. Every committee has a way of working: the objectives listed in this announcement would go down really well with the C++ committee (which already does many of the points listed), but the Fortran committee don’t operate this way.
The language standards world appears to be very similar to the open source world, in that they are both driven by the people who do the work. One person can have a big impact in the open source world, simply by doing the work, but in the language standards world there is voting (people can vote in the open source world by using software or not). One person can write papers and propose lots of additions to a standard, but the agreement of committee members is needed before any wording is added to a draft standard, which eventually goes out for a round of voting by national bodies.
Over the years I have seen several people on a standards committee starting out very enthusiastic, writing proposals and expounding them at meetings; then after a year or two becoming despondent because nothing has happened. If committee members don’t like your proposal (or choose to spend their time on other proposals), they do nothing. A majority doing nothing is enough to stop something happening.
Once a language has become established, many of its users want the committee to move slowly. Compiler vendors don’t want to spend all their time keeping up with language updates (which rarely help sell more product), and commercial users don’t want the hassle of having to spend time working out how a new standard might impact them (having zero impact on existing is a common aim of language committees).
The young, the enthusiastic, and magazines looking to sell clicks are excited by change. An ISO language committee is generally not the place to find it.
Update
INCITS have nominated the current chair for the next three-year term.
Beta release of data analysis chapters: Evidence-based software engineering
When I started my evidence-based software engineering book, nobody had written a data analysis book for software developers, so I had to write one (in fact, a book on this topic has still to be written). When I say “I had to write one”, what I mean is that the 200 pages in the second half of my evidence-based software engineering book contains a concentrated form of such a book.
This 200 pages is now on beta release (it’s 186 pages, if the bibliography is excluded); chapters 8 to 15 of the draft pdf. Originally I was going to wait until all the material was ready, before making a beta release; the Coronavirus changed my plans.
Here is your chance to learn a new skill during the lockdown (yes, these are starting to end; my schedule has not changed, I’m just moving with the times).
All the code+data is available for you to try out any ideas you might have.
The software engineering material, the first half of the book, is also part of the current draft pdf, and the polished form should be available on beta release in about 6 weeks.
If you have a comment or find a problem, either email me or raise an issue on the book’s Github page.
Yes, a few figures and tables still bump into each other. I’m loath to do very fine-tuning because things will shuffle around a bit with minor changes to the words.
I’m thinking of running some online sessions around each chapter. Watch this space for information.
Predicting the future with data+logistic regression
Predicting the peak of data fitted by a logistic equation is attracting a lot of attention at the moment. Let’s see how well we can predict the final size of a software system, in lines of code, using logistic regression (code+data).
First up is the size of the GNU C library. This is not really a good test, since the peak (or rather a peak) has been reached.
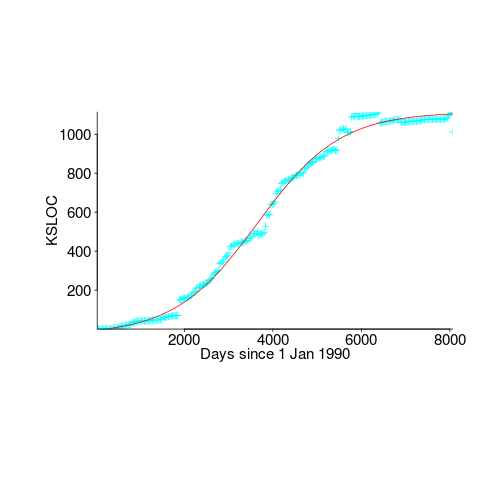
We need a system that has not yet reached an easily recognizable peak. The Linux kernel has been under development for many years, and lots of LOC counts are available. The plot below shows a logistic equation fitted to the kernel data, assuming that the only available data was up to day: 2,900, 3,650, 4,200, and 5,000+. Can you tell which fitted line corresponds to which number of days?
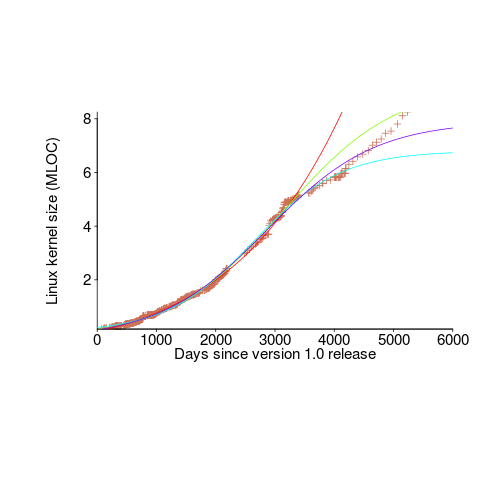
The underlying ‘problem’ is that we are telling the fitting software to fit a particular equation; the software does what it has been told to do, and fits a logistic equation (in this case).
A cubic polynomial is also a great fit to the existing kernel data (red line to the left of the blue line), and this fitted equation can be extended into future (to the right of the blue line); dotted lines are 95% confidence bounds. Do any readers believe the future size of the Linux kernel predicted by this cubic model?
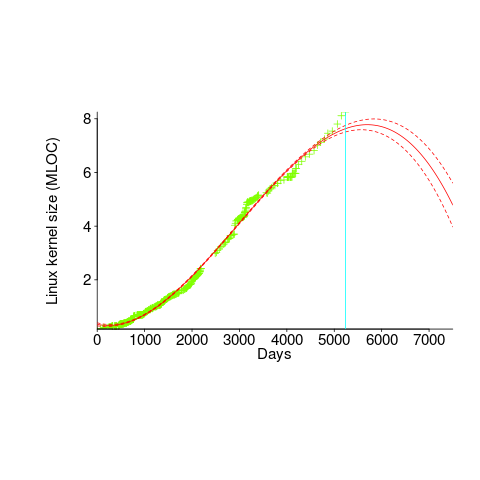
Predicting the future requires lots of data on the underlying processes that drive events. Modeling events is an iterative process. Build a model, check against reality, adjust model, rinse and repeat.
If the COVID-19 experience trains people to be suspicious of future predictions made by models, it will have done something positive.
Motzkin paths and source code silhouettes
Consider a language that just contains assignments and if-statements (no else arm). Nesting level could be used to visualize programs written in such a language; an if represented by an Up step, an assignment by a Level step, and the if-terminator (e.g., the } token) by a Down step. Silhouettes for the nine possible four line programs are shown in the figure below (image courtesy of Wikipedia). I use the term silhouette because the obvious terms (e.g., path and trace) have other common usage meanings.

How many silhouettes are possible, for a function containing 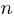 statements? Motzkin numbers provide the answer; the number of silhouettes for functions containing from zero to 20 statements is: 1, 1, 2, 4, 9, 21, 51, 127, 323, 835, 2188, 5798, 15511, 41835, 113634, 310572, 853467, 2356779, 6536382, 18199284, 50852019. The recurrence relation for Motzkin numbers is (where
statements? Motzkin numbers provide the answer; the number of silhouettes for functions containing from zero to 20 statements is: 1, 1, 2, 4, 9, 21, 51, 127, 323, 835, 2188, 5798, 15511, 41835, 113634, 310572, 853467, 2356779, 6536382, 18199284, 50852019. The recurrence relation for Motzkin numbers is (where 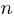 is the total number of steps, i.e., statements):
is the total number of steps, i.e., statements):
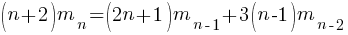
Human written code contains recurring patterns; the probability of encountering an if-statement, when reading code, is around 17% (at least for the C source of some desktop applications). What does an upward probability of 17% do to the Motzkin recurrence relation? For many years I have been keeping my eyes open for possible answers (solving the number theory involved is well above my mathematics pay grade). A few days ago I discovered weighted Motzkin paths.
A weighted Motzkin path is one where the Up, Level and Down steps each have distinct weights. The recurrence relationship for weighted Motzkin paths is expressed in terms of number of colored steps, where: 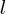 is the number of possible colors for the Level steps, and
is the number of possible colors for the Level steps, and  is the number of possible colors for Down steps; Up steps are assumed to have a single color:
is the number of possible colors for Down steps; Up steps are assumed to have a single color:
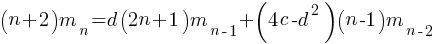
setting: 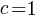 and
and 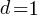 (i.e., all kinds of step have one color) recovers the original relation.
(i.e., all kinds of step have one color) recovers the original relation.
The different colored Level steps might be interpreted as different kinds of non-nesting statement sequences, and the different colored Down steps might be interpreted as different ways of decreasing nesting by one (e.g., a goto statement).
The connection between weighted Motzkin paths and probability is that the colors can be treated as weights that add up to 1. Searching on “weighted Motzkin” returns the kind of information I had been looking for; it seems that researchers in other fields had already discovered weighted Motzkin paths, and produced some interesting results.
If an automatic source code generator outputs the start of an if statement (i.e., an Up step) with probability 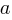 , an assignment (i.e., a Level step) with probability
, an assignment (i.e., a Level step) with probability 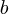 , and terminates the
, and terminates the if (i.e., a Down step) with probability 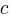 , what is the probability that the function will contain at least
, what is the probability that the function will contain at least 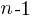 statements? The answer, courtesy of applying Motzkin paths in research into clone cell distributions, is:
statements? The answer, courtesy of applying Motzkin paths in research into clone cell distributions, is:
![P_n=sum{i=0}{delim{[}{(n-2)/2}{]}}(matrix{2}{1}{{n-2} {2i}})C_{2i}a^{i}b^{n-2-2i}c^{i+1} P_n=sum{i=0}{delim{[}{(n-2)/2}{]}}(matrix{2}{1}{{n-2} {2i}})C_{2i}a^{i}b^{n-2-2i}c^{i+1}](https://shape-of-code.com/wp-content/plugins/wpmathpub/phpmathpublisher/img/math_960.5_57086dac25a2ff31c2230f0791800e35.png)
where: 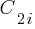 is the
is the 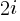 ‘th Catalan number, and that
‘th Catalan number, and that [...] is a truncation; code for an implementation in R.
In human written code we know that 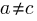 , because the number of statements in a compound-statement roughly has an exponential distribution (at least in C).
, because the number of statements in a compound-statement roughly has an exponential distribution (at least in C).
There has been some work looking at the number of peaks in a Motzkin path, with one formula for the total number of peaks in all Motzkin paths of length n. A formula for the number of paths of length 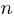 , having
, having 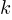 peaks, would be interesting.
peaks, would be interesting.
Motzkin numbers have been extended to what is called higher-rank, where Up steps and Level steps can be greater than one. There are statements that can reduce nesting level by more than one, e.g., breaking out of loops, but no constructs increase nesting by more than one (that I can think of). Perhaps the rather complicated relationship can be adapted to greater Down steps.
Other kinds of statements can increase nesting level, e.g., for-statements and while-statements. I have not yet spotted any papers dealing with the case where an Up step eventually has a corresponding Down step at the appropriate nesting level (needed to handle different kinds of nest-creating constructs). Pointers welcome. A related problem is handling if-statements containing else arms, here there is an associated increase in nesting.
What characteristics does human written code have that results in it having particular kinds of silhouettes? I have been thinking about this for a while, but have no good answers.
If you spot any Motzkin related papers that you think could be applied to source code analysis, please let me know.
Update
A solution to the Number of statement sequences possible using N if-statements problem.
Comments on the COVID-19 model source code from Imperial
At the end of March a paper modelling the impact of various scenarios on the spread of COVID-19 infections, by the MRC Centre for Global Infectious Disease Analysis at Imperial College, appears to have influenced the policy of the powers that be. This group recently started publishing their modelling code on GitHub (good for them).
Most of my professional life has been spent analyzing other peoples’ code, for one reason or another (mostly Fortran, then Pascal, and then C). I had heard that the Imperial software was written in C, but the released code is written in R (as of six hours ago, there is the start of a Python version). Ok, I can work with R, but my comments will be general, since I don’t have lots of in depth experience reading R code.
The code comes from a research context, and is evolving, i.e., some amount of messiness is to be expected.
There is not a lot of code to talk about (248 lines setting things up, 111 lines for a Stan model, 371 lines of plotting code, and 85 lines of utility code). The analysis is performed by creating a model using the Stan statistical inference language (in which the high level structure of the problem is specified, compiled to a lower level form and then run; the Stan language is very similar to R). These days, lots of problems are coded using a relatively small number of lines that call fancy libraries to do the heavy lifting. It is becoming rare to have to write tens of thousands of lines of code to solve a problem.
I have two points to make about the code, all designed to reduce the likelihood of mistakes being made by the person working on the source. These points mainly apply to the Stan code, because that is where the important stuff happens, but are equally applicable to all code.
- Numeric literals are embedded in the code, values include:
2.4,1.0,0.5,0.03,1e-5, and1e-9. These values obviously mean something to the person who wrote the code, and they can probably be interpreted by experts in the spread of virus infections. But why are they scattered about the code, rather than appearing together (as a sequence of assignments to variables with meaningful names)? Having all the constants in one place makes it easier to spot when a mistake has been made, e.g., one value has been changed without a corresponding change in another value; it also makes it easier for people new to the code to figure out what is going on, - when commenting out code, make it very obvious, e.g., have
/**********************on its own line, and*****************************/on its own line. Using just/*and*/makes it easy to miss that code has been commented out.
Why have they started a Python implementation? Perhaps somebody on the team is more comfortable working with Python (when deadlines loom, it is always best to go with what you know).
Having both an R and Python version is good, in that coding mistakes are likely to show up as inconsistencies in the results produced. It’s always good to have the output of two independently written programs to compare (apart from the fact it may cost twice as much).
The README mentions performance issues. I imagine that most of the execution time is spent in the Stan code, so R vs. Python is not a performance issue.
Any reader with expertise tuning Stan models for performance might like to check out the code. I’m sure the Imperial folk would be happy to hear about worthwhile speed-ups.
Update
The R source code of the EuroMOMO model, which aims to “… explain number of deaths by a baseline, influenza activity and extreme ambient temperature.”
Influential programming languages: some of the considerations
Which programming languages have been the most influential?
Let’s define an influential language as one that has had an impact on lots of developers. What impact might a programming language have on developers?
To have an impact a language needs to be used by lots of people, or at least have a big impact on a language that is used by lots of people.
Figuring out the possible impacts a language might have had is very difficult, requiring knowledge of different application domains, software history, and implementation techniques. The following discussion of specific languages illustrate some of the issues.
Simula is an example of a language used by a handful of people, but a few of the people under its influence went on to create Smalltalk and C++. Some people reacted against the complexity of Algol 68, creating much simpler languages (e.g., Pascal), while others thought some of its feature were neat and reused them (e.g., Bourne shell).
Cobol has been very influential, at least within business computing (those who have not worked in business computing complain about constructs handling uses that it was not really designed to handle, rather than appreciating its strengths in doing what it was designed to do, e.g., reading/writing and converting a wide range of different numeric data formats). RPG may have been even more influential in this usage domain (all businesses have to specific requirements on formatting reports).
I suspect that most people could not point to the major influence C has had on almost every language since. No, not the use of { and }; if a single character is going to be used as a compound statement bracketing token, this pair are the only available choice. Almost every language now essentially uses C’s operator precedence (rather than Fortran‘s, which is slightly different; R follows Fortran).
Algol 60 has been very influential: until C came along it was the base template for many languages.
Fortran is still widely used in scientific and engineering software. Its impact on other languages may be unknown to those involved. The intricacies of floating-point arithmetic are difficult to get right, and WG5 (the ISO language committee, although the original work was done by the ANSI committee, J3). Fortran code is often computationally intensive, and many optimization techniques started out optimizing Fortran (see “Optimizing Compilers for Modern Architectures” by Allen and Kennedy).
BASIC showed how it was possible to create a usable interactive language system. The compactness of its many, and varied, implementations were successful because they did not take up much storage and were immediately usable.
Forth has been influential in the embedded systems domain, and also people fall in love with threaded code as an implementation technique (see “Threaded Interpretive Languages” by Loeliger).
During the mid-1990s the growth of the Internet enabled a few new languages to become widely used, e.g., PHP and Javascript. It’s difficult to say whether these were more influenced by what their creators ate the night before or earlier languages. PHP and Javascript are widely used, and they have influenced the creation of many languages designed to fix their myriad of issues.
Coronavirus: a silver lining for evidence-based software engineering?
People rarely measure things in software engineering, and when they do they rarely hang onto the measurements; this might also be true in many other work disciplines.
When I worked on optimizing compilers, I used to spend time comparing code size and performance. It surprised me that many others in the field did not, they seemed to think that if they implemented an optimization, things would get better and that was it. Customers would buy optimizers without knowing how long their programs took to do a task, they seemed to want things to go faster, and they had some money to spend buying stuff to make them feel that things had gotten faster. I quickly learned to stop asking too many questions, like “how fast does your code currently run”, or “how fast would you like it to run”. Sell them something to make them feel better, don’t spoil things by pointing out that their code might already be fast enough.
In one very embarrassing incident, the potential customer was interested in measuring performance, and my optimizer make their important program go slower! As best I could tell, the size of the existing code just fitted in memory, and optimizing for performance made it larger; the system started thrashing and went a lot slower.
What question did potential customers ask? They usually asked whether particular optimizations were implemented (because they had read about them someplace). Now some of these optimizations were likely to make very little difference to performance, but they were easy to understand and short enough to write articles about. And, yes. I always made sure to implement these ‘minor’ optimizations purely to keep customers happy (and increase the chances of making a sale).
Now I work on evidence-based software engineering, and developers rarely measure things, and when they do they rarely hang onto the measurements. So many people have said I could have their data, if they had it!
Will the Coronavirus change things? With everybody working from home, management won’t be able to walk up to developers and ask what they have been doing. Perhaps stuff will start getting recorded more often, and some of it might be kept.
A year from now it might be a lot easier to find information about what developers do. I will let you know next year.
Exercises in Programming Style: the python way
Exercises in Programming Style by Cristina Lopes is an interesting little book.
The books I have previously read on programming style pick a language, and then write various programs in that language using different styles, idioms, or just following quirky rules, e.g., no explicit loops, must use sets, etc. “Algorithms in Snobol 4” by James F. Gimpel is a fascinating read, but something of an acquired taste.
EPS does pick a language, Python, but the bulk of the book is really a series of example programs illustrating a language feature/concept that is central to a particular kind of language, e.g., continuation-passing style, publish-subscribe architecture, and reflection. All the programs implement the same problem: counting the number of occurrences of each word in a text file (Jane Austin’s Pride and Prejudice is used).
The 33 chapters are each about six or seven pages long, and contain a page or two or code. Everything is very succinct, and does a good job of illustrating one main idea.
While the first example does not ring true, things quickly pick up and there are lots of interesting insights to be had. The first example is based on limited storage (1,024 bytes), and just does not make efficient use of the available bits (e.g., upper case letters can be represented using 5-bits, leaving three unused bits or 37% of available storage; a developer limited to 1K would not waste such a large amount of storage).
Solving the same problem in each example removes the overhead of having to learn what is essentially housekeeping material. It also makes it easy to compare the solutions created using different ideas. The downside is that there is not always a good fit between the idea being illustrated and the problem being solved.
There is one major omission. Unstructured programming; back in the day it was just called programming, but then structured programming came along, and want went before was called unstructured. Structured programming allowed a conditional statement to apply to multiple statements, an obviously simple idea once somebody tells you.
When an if-statement can only be followed by a single statement, that statement has to be a goto; an if/else is implemented as (using Fortran, I wrote lots of code like this during my first few years of programming):
IF (I .EQ. J) GOTO 100 Z=1 GOTO 200 100 Z=2 200 |
Based on the EPS code in chapter 3, Monolithic, an unstructured Python example might look like (if Python supported goto):
for line in open(sys.argv[1]): start_char = None i = 0 for c in line: if start_char != None: goto L0100 if not c.isalnum(): goto L0300 # We found the start of a word start_char = i goto L0300 L0100: if c.isalnum(): goto L0300 # We found the end of a word. Process it found = False word = line[start_char:i].lower() # Ignore stop words if word in stop_words: goto L0280 pair_index = 0 # Let's see if it already exists for pair in word_freqs: if word != pair[0]: goto L0210 pair[1] += 1 found = True goto L0220 L0210: pair_index += 1 L0220: if found: goto L0230 word_freqs.append([word, 1]) goto L0300 L0230: if len(word_freqs) <= 1: goto L0300: # We may need to reorder for n in reversed(range(pair_index)): if word_freqs[pair_index][1] <= word_freqs[n][1]: goto L0240 # swap word_freqs[n], word_freqs[pair_index] = word_freqs[pair_index], word_freqs[n] pair_index = n L0240: goto L0300 L0280: # Let's reset start_char = None L0300: i += 1 |
If you do feel a yearning for the good ol days, a goto package is available, enabling developers to write code such as:
from goto import with_goto @with_goto def range(start, stop): i = start result = [] label .begin if i == stop: goto .end result.append(i) i += 1 goto .begin label .end return result |
Source code chapter of ‘evidence-based software engineering’ reworked
The Source code chapter of my evidence-based software engineering book has been reworked (draft pdf).
When writing the first version of this chapter, I was not certain whether source code was a topic warranting a chapter to itself, in an evidence-based software engineering book. Now I am certain. Source code is the primary product delivery, for a software system, and it is takes up much of the available cognitive effort.
What are the desirable characteristics that source code should have, to minimise production costs per unit of functionality? This is what an evidence-based chapter on source code is all about.
The release of this chapter completes my second pass over the material. Readers will notice the text still contains ... and ?‘s. The third pass will either delete these, or say something interesting (I suspect mostly the former, because of lack of data).
Talking of data, February has been a bumper month for data (apologies if you responded to my email asking for data, and it has not appeared in this release; a higher than average number of people have replied with data).
The plan is to spend a few months getting a beta release ready. Have the beta release run over the summer, with the book in the shops for Christmas.
I’m looking at getting a few hundred printed, for those wanting paper.
The only publisher that did not mind me making the pdf freely available was MIT Press. Unfortunately one of the reviewers was foaming at the mouth about the things I had to say about software engineering researcher (it did not help that I had written a blog post containing a less than glowing commentary on academic researchers, the week of the review {mid-2017}); the second reviewer was mildly against, and the third recommended it.
If any readers knows the editors at MIT Press, do suggest they have another look at the book. I would rather a real publisher make paper available.
Next, getting the ‘statistics for software engineers’ second half of the book ready for a beta release.
The wisdom of the ancients
The software engineering ancients are people like Halstead and McCabe, along with less well known ancients (because they don’t name anything after them) such as Boehm for cost estimation, Lehman for software evolution, and Brooks because of a book; these ancients date from before 1980.
Why is the wisdom of these ancients still venerated (i.e., people treat them as being true), despite the evidence that they are very inaccurate (apart from Brooks)?
People hate a belief vacuum, they want to believe things.
The correlation between Halstead’s and McCabe’s metrics, and various software characteristics is no better than counting lines of code, but using a fancy formula feels more sophisticated and everybody else uses them, and we don’t have anything more accurate.
That last point is the killer, in many (most?) cases we don’t have any metrics that perform better than counting lines of code (other than taking the log of the number of lines of code).
Something similar happened in astronomy. Placing the Earth at the center of the solar system results in inaccurate predictions of where the planets are going to be in the sky; adding epicycles to the model helps to reduce the error. Until Newton came along with a model that produced very accurate results, people stuck with what they knew.
The continued visibility of COCOMO is a good example of how academic advertising (i.e., publishing papers) can keep an idea alive. Despite being more sophisticated, the Putnam model is not nearly as well known; Putnam formed a consulting company to promote this model, and so advertised to a different market.
Both COCOMO and Putnam have lines of code as an integral component of their models, and there is huge variability in the number of lines written by different people to implement the same functionality.
People tend not to talk about Lehman’s quantitative work on software evolution (tiny data set, and the fitted equation is very different from what is seen today). However, Lehman stated enough laws, and changed them often enough, that it’s possible to find something in there that relates to today’s view of software evolution.
Brooks’ book “The Mythical Man-Month” deals with project progress and manpower; what he says is timeless. The problem is that while lots of people seem happy to cite him, very few people seem to have read the book (which is a shame).
There is a book coming out this year that provides lots of evidence that the ancient wisdom is wrong or at best harmless, but it does not contain more accurate models to replace what currently exists 🙁
Recent Comments