The Shape of Code

When estimating the time needed to implement a task, the time previously needed to implement similar tasks provides useful guidance. The implementation time for these previous tasks may itself be estimated, because the actual time was not measured or this information is currently unavailable.

How accurate are developer time estimates of previously completed tasks?

I am not aware of any software related dataset of estimates of previously completed tasks (it’s hard enough finding datasets containing information on the actual implementation time). However, I recently found the paper Dynamics of retrospective timing: A big data approach by Balcı, Ünübol, Grondin, Sayar, van Wassenhove, and Wittmann. The data analysed comes from a survey questionnaire, where 24,494 people estimated the how much time they had spent answering the questions, along with recording the current time at the start/end of the questionnaire. The supplementary data is in MATLAB format, and is also available as a csv file in the Blursday database (i.e., RT_Datasets).

Some of the behavior patterns seen in software engineering estimates appear to be general human characteristics, e.g., use of round numbers. An analysis of the estimation performance of a wide sample of the general population could help separate out characteristics that are specific to software engineering and those that apply to the general population.

The following table shows the percentage of answers giving a particular Estimate and Actual time, in minutes. Over 60% of the estimates are round numbers. Actual times are likely to be round numbers because people often give a round number when asked the time (code+data):

   Minutes    Estimate    Actual
     20          18%       8.5%
     15          15%       5.3%
     30          12%       7.6%
     25          10%       6.2%
     10           7.7%     2.1%

I was surprised to see that the authors had fitted a regression model with the Actual time as the explanatory variable and the Estimate as the response variable. The estimation models I have fitted always have the roles of these two variables reversed. More of this role reversal difference below.

The equation fitted to the data by the authors is (they use the term Elapsed, for consistency with other blog articles I continue to use Actual; code+data):

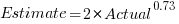
This equation says that, on average, for shorter Actual times the Estimate is higher than the Actual, while for longer Actual times the average Estimate is lower.

Switching the roles of the variables, I expected to see a fitted model whose coefficients are somewhat similar to the algebraically transformed version of this equation, i.e., 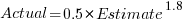. At the very least, I expected the exponent to be greater than one.

Surprisingly, the equation fitted with the variables roles reversed is very similar, i.e., the equations are the opposite of each other:

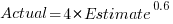
This equation says that, on average, for shorter Estimate times the Actual time is higher than the Estimate, while for longer Estimate times the average Actual is lower, i.e., the opposite behavior specifie dby the earlier equation.

I spent some time trying to understand how it was possible for data to be fitted such that (x ~ y) == (y ~ x), even posting a question to Cross Validated. I might, in a future post, discuss the statistical issues behind this behavior.

So why did the authors of this paper treat Actual as an explanatory variable?

After a flurry of emails with the lead author, Fuat Balcı (who was very responsive to my questions), where we both doubled checked the code/data and what we thought was going on, Fuat answered that (quoted with permission):

“The objective duration is the elapsed time (noted by the experimenter based on a clock reading), and the estimate is the participant’s response. According to the psychophysical approach the mapping between objective and subjective time can be defined by regressing the subjective estimates of the participants on the objective duration noted by the experimenter. Thus, if your research question is how human’s retrospective experience of time changes with the duration of events (e.g., biases in time judgments), the y-axis should be the participant’s response and the x-axis should be the actual duration.”

This approach has a logic to it, and is consistent with the regression modelling done by other researchers who study retrospective time estimation.

So which modelling approach is correct, and are people overestimating or underestimating shorter actual time durations?

Going back to basics, the structure of this experiment does not produce data that meets one of the requirements of the statistical technique we are both using (ordinary least squares) to fit a regression model. To understand why ordinary least squares, OLS, is not applicable to this data, it’s necessary to delve into a technical detail about the mathematics of what OLS does.

The equation actually fitted by OLS is: 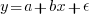, where 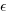is an error term (i.e., ‘noise’ caused by all the effects other than ). The value of is assumed to be exact, i.e., not contain any ‘noise’.

Usually, in a retrospective time estimation experiment, subjects hear, for instance, a sound whose duration is decided in advance by the experimenter; subjects estimate how long each sound lasted. In this experimental format, it makes sense for the Actual time to appear on the right-hand-side as an explanatory variable and for the Estimate response variable on the left-hand-side.

However, for the questionnaire timing data, both the Estimate and Actual time are decided by the person giving the answers. There is no experimenter controlling one of the values. Both the Estimate and Actual values contain ‘noise’. For instance, on a different day a person may have taken more/less time to actually answer the questionnaire, or provided a different estimate of the time taken.

The correct regression fitting technique to use is errors-in-variables. An errors-in-variables regression fits the equation: 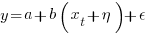, where: 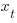is the true value of and 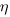is its associated error. A selection of packages are available for fitting a variety of errors-in-variables models.

I regularly see OLS used in software engineering papers (including mine) where errors-in-variables is the technically correct technique to use. Researchers are either unaware of the error issues or assuming that the difference is not important. The few times I have fitted an errors-in-variables model, the fitted coefficients have not been much different from those fitted by an OLS model; for this dataset the coefficient difference is obviously important.

The complication with building an errors-in-variables model is that values need to be specified for the error terms 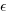and 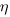. With OLS the value of 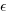is produced as part of the fitting process.

How might the required error values be calculated?

If some subjects round reported start/stop times, there may not be any variation in reported Actual time, or it may jump around in 5-minute increments depending on the position of the minute hand on the clock.

Learning researchers have run experiments where each subject performs the same task multiple times. Performance improves with practice, which makes it difficult to calculate the likely variability in the first-time performance. If we assume that performance is skill based, the standard deviation of all the subjects completing within a given timeframe could be used to calculate an error term.

With 60% of Estimates being round numbers, there might not be any variation for many people, or perhaps the answer given will change to a different round number. There is Estimate data for different, future tasks, and a small amount of data for the same future tasks. There is data from many retrospective studies using very short time intervals (e.g., tens of seconds), which might be applicable.

We could simply assume that the same amount of error is present in each variable. Deming regression is an errors-in-variables technique that supports this approach, and does not require any error values to be specified. The following equations have been fitted using Deming regression (code+data):

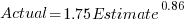
and

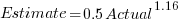
While these two equations are consistent with each other, we don’t know if the assumption of equal errors in both variables is realistic.

What next?

Hopefully it will be possible to work out reasonable error values for the Actual/Estimate times. Fitting a model using these values will tell us wether any over/underestimating is occurring, and the associated span of time durations.

I also need to revisit the analysis of software task estimation times.