Archive
C compilers on PR1ME computers
At the start of this week I knew almost nothing about the C compilers running on PR1ME computers (every now and again I check bitsavers for newly scanned C compiler manuals).
On Tuesday I spotted the source of the Georgia Tech C Compiler for Prime Computers (which was believed lost until two 35-years old mag tapes were found); the implementation language is Ratfor.
I posted the information to the comp.compilers newsgroup, and in the ensuing posts I learned about Dennis Boone’s collection of scanned PR1ME manuals, including a C compiler user guide. This C user’s guide is for the Conboy/Pacer software compiler, not the one whose sources I linked to above.
The PR1ME C compiler has the usually assortment of vendor extensions, and missing features, of the kind that might be found in any C compiler from the 1980s; however, there is a larger than usual collection of infrequently seen characteristics. I spotted the following during a quick read through the manual:
- addresses point to 16-bit words (not 8-bit bytes). The implementers could have chosen to define a
charas 16-bit (i.e., defining the standard macroCHAR_BITas 16), but they went with 8-bit chars. Handling 8-bit chars on a word addressed processor means that pointers tocharhave to include a bit specifying which half of the 16-bits they are pointing to. Some Cray computers had the same issue, except their words contained 64 bits, so more offset bits had to be stored in pointers.The definition of an object having type
charoccupies 8 bits of a word, no other object is allocated in the other 8 bits; arrays ofcharare packed, two chars to a word. - ASCII characters have the top-bit set (the manual phrases this as “The basic character set … ASCII 7-bit set (called ASCII-7), with the eighth bit turned on.”). The C standard requires that the ten digit characters have continuous values, and that the basic character set be representable in a char.
- a pointer type may contain more bits than any supported integer type, i.e., 48-bit pointer and 32-bit integer. PR1ME cpus supported a dizzying array of different modes and instruction sets; some later instruction sets/modes support 48-bit pointers.
- “On some other machines, you may write code in which a function is called with more or fewer parameters than the function actually expects. Such code may work correctly on the 50 Series, but only if the missing or extra parameter is never referenced.”
- “On some other machines, programs run correctly if function return value data types are left undeclared. … If this function is not explicitly defined as returning a pointer, the default return value is type int. Such a program may run correctly on some machines, but not on a 50 Series machine.”
These characteristics combine to make the PR1ME a very unfriendly environment for C programs.
C programmers have a culture, the C way of doing things (these cultures exist for all languages), and the characteristics of this (and perhaps other) PR1ME C compilers run counter to this culture in many ways.
I’m not saying that C culture is good or bad, just that it exists and PR1ME is a very poor fit.
What elements of C culture clash with the PR1ME implementation?
There is an expectation that when two objects having char type are defined sequentially (e.g., char a, b;), it will be possible to access b by adding 1 to a pointer to a (as if the definition had been written as: char a[2];). Yes, this practice is now frowned upon, but it was once considered ok (at least in some circles). On PR1ME the two definitions are not equivalent, from the pointer arithmetic point of view.
Very many developers assume that C characters use ASCII. Most of the time they do, but they are not required to; EBCDIC being perhaps the most well known alternative. At least in the PR1ME encoding the alphabetic characters have contiguous values, which they don’t in EBCDIC. But setting the top bit, hmmm….
The assumption that sizeof(int) == sizeof(pointer_type) is endemic in 1980s code, and much code in later decades; many (not so young) C programmers will tell you the story of the first time they had to switch mind-sets to: sizeof(long) == sizeof(pointer_type). Not having a 48-bit integer type is a bit of a killer for C on PR1ME, as we will find out.
PR1MOS, the vendor operating system, uses a function call stack layout that assumes a function definition specifies exactly how the function will be called, e.g., the number and type of parameters, and the return type.
In the early decades of C, programmers were very lax about specifying exactly what arguments a function expected, and that no return type implicitly specified an int return type (and since everybody knew that sizeof(int) == sizeof(pointer_type), this meant that it was not necessary to specify pointer return types).
During development, having the program raise an exception, or whatever the behavior was, when a function call did not match the defined type of the function, is useful; it improves program reliability by catching those cases that might work as expected a lot of the time, but not all the time.
A lot of existing code was created on systems that were forgiving of function call/definition mismatches. Such C source is unlikely to just compile and run under PR1MOS, i.e., porting other peoples programs is likely to be a time-consuming process.
Plotting artifacts when the axis involves lines of code
While reading a report from the very late Rome period, the plot below caught my attention (the regression line was not in the original plot). The points follow a general trend, suggesting that when implementing a module, lines of code written per man-hour increases as the size of the module increases (in LOC). There are explanations for such behavior: perhaps module implementation time is mostly think-time that is independent of LOC, or perhaps larger modules contain more lines that can be quickly implemented (code+data).
Then I realised that the pattern of points was generated by a mathematical artifact. Can you spot the artifact?
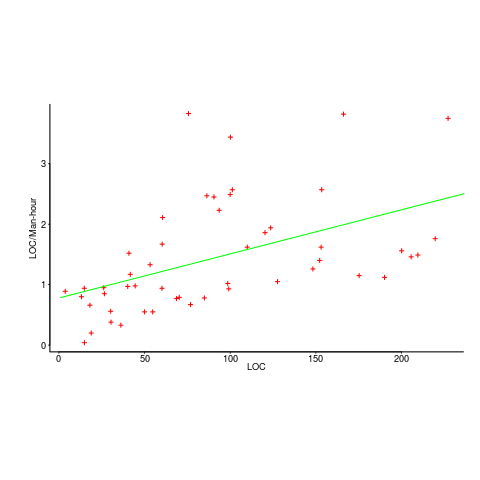
The x-axis shows LOC, and the y-axis shows LOC/man-hour. Just plotting LOC against LOC would produce a row of points along a straight line, and if we treat dividing by man-hours as roughly equivalent to dividing by a random number (which might have some correlation with LOC), the result is points scattered around a line going up to the right.
If LOC-per-hour were constant, the points would form a horizontal line across the plot.
In the below left plot, from a different report (whose axis are function-points, and function-points implemented per month), the author has fitted a line, and it is close to horizontal (suggesting that the mean FP-per-month is constant).
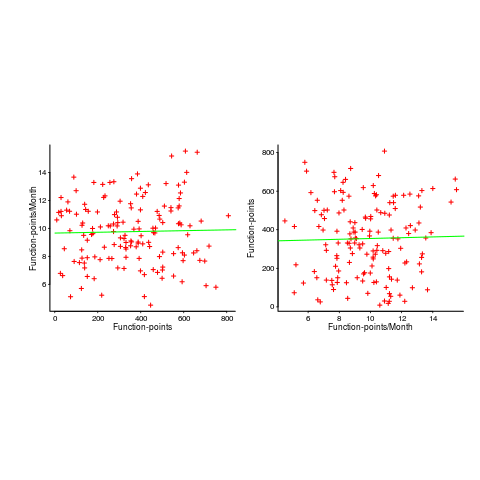
In fact the points are essentially random, and the line is a terrible fit (just how terrible is shown by switching the axis and refitting the line, above right; the refitted line should be vertical, but is horizontal. There is no connection between FP and FP-per-month, which is a good thing because the creators of function-points intended this to be true).
What process might generate this random scattering, rather than the trend seen in the first plot? If the implementation time was proportional to both the number of FP and some uniform random component, then the FP/time ratio would have the pattern seen.
The plots below show module size (in LOC) against man-hour (left) and FP against months (right):
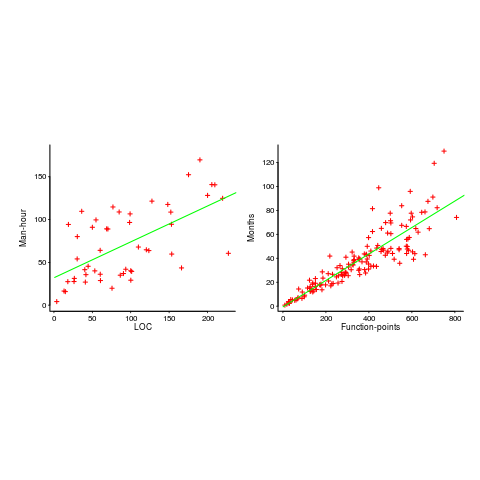
The module-LOC points are all over the place, while the FP points look as-if they are roughly consistent. Perhaps the module-LOC measurements came from a wide variety of sources, and we should not expect a visually pleasant trend.
Plotting LOC against LOC appears in other guises. Perhaps the most common being plotting fault-density against LOC; fault-density is generally calculated as faults/LOC.
Of course the artifacts also occur when plotting other kinds of measurements. Lines of code happens to be a commonly plotted quantity (at least in software engineering).
Team DNA-impersonators create a business plan
This weekend I was at the Hack the Police hackthon, sponsored by the Metropolitan Police+other organizations. My plan was to find an interesting problem to help solve, using the data we were told would be available. My previous experience with crime data is that there is not enough of it to allow reliable models to be built, this is a good thing in that nobody wants lots of crime. Talking to a Police intelligence officer, the publicly available data contained crimes (i.e., a court case had found somebody guilty), not reported incidents, and was not large enough to build allow a good model to be built.
Looking for a team to join, I got talking to Joe and Rebecca. Joe had discovered a very interesting possible threat to the existing DNA matching technique, and they were happy for me to join them analyzing this threat model; team DNA-impersonators was go.
Some background (Joe and Rebecca are the team’s genetic experts, I’m a software guy who has read a few books on the subject; all the mistakes in this post are mine). The DNA matching technique used by the Police is based on 17 specific sequences (each around 100 bases, known as loci), within the human genome (which contains around 3 billion bases).
There are companies who synthesize sequences of DNA to order. I knew that machines for doing this existed, but I did not know it was possible to order a bespoke sequence online, and how inexpensive it was.
Some people have had their DNA sequenced, and have allowed it to be published online; Steven Pinker is the most famous person I could find, whose DNA sequence is available online (link not given; it requires work+luck to find). The Personal Genome Projects aims to sequence and make available the complete genomes of 100,000 volunteers (the UK arm of this project is on hold because of lack of funding; master criminals in the UK have a window of opportunity: offer to sponsor the project on condition that their DNA is included in the public data set).
How much would it cost to manufacture bottles of spray-on Steven Pinker DNA? Is there a viable business model selling Pinker No. 5?
The screenshot below shows a quote for 2-nmol of DNA for the sequence of 100 bases that are one of the 17 loci used in DNA matching. This order is for concentrated DNA, and needs to be diluted to the level likely to be found as residue at a crime scene. Joe calculated that 2-nmol can be diluted to produce 60-liters of usable ‘product’.
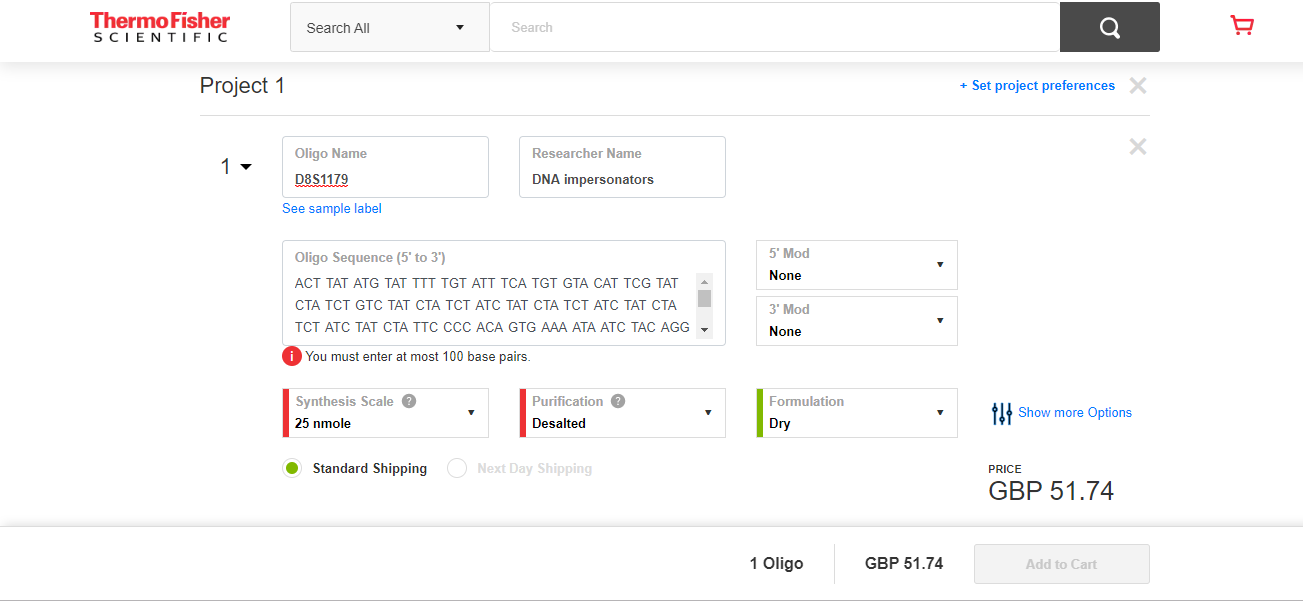
There was not enough time to obtain sequences for the other 16-loci, and get quotes for them. Information on the 17-loci used for DNA matching is available in research papers; a summer job for a PhD student to sort out the details.
The concentrate from the 17-loci dilutes to 60-liters. Say each spray-on bottle contains 100ml, then an investment of £800 (plus researcher time) generates enough liquid for 600-bottles of Pinker No. 5.
What is the pricing model? Is there a mass market (e.g., Hong Kong protesters wanting to be anonymous), or would it be more profitable to target a few select clients? Perhaps Steven Pinker always wanted to try his hand at safe-cracking in his spare time, but was worried about leaving DNA evidence behind; he might be willing to pay to have the market flooded, so Pinker No. 5 residue becomes a common occurrence at crime scenes (allowing him to plausible claim that any crime scene DNA matches were left behind by other people).
Some of the police officers at the hack volunteered that they knew lots of potential customers; the forensics officer present was horrified.
Before the 1980s, DNA profiling was not available. Will the 2020s be the decade in which DNA profiling ceases being a viable tool for catching competent criminals?
High quality photocopiers manufacturers are required to implement features that make it difficult for people to create good quality copies of paper currency.
What might law enforcement do about this threat to the viability of DNA profiling?
Ideas include:
- Requiring companies in the bespoke DNA business to report suspicious orders. What is a suspicious order? Are enough companies in business to make it possible to order each of the 17-loci from a different company (we think so)?
- Introducing laws making it illegal to be in possession of diluted forms of other people’s DNA (with provisions for legitimate uses).
- Attacking the economics of the Pinker No. 5 business model by having more than 17-loci available for use in DNA matching. Perhaps 1,000 loci could be selected as potential match sites, with individual DNA testing kits randomly testing 17 (or more) from this set.
Natural elimination, or the survival of the good enough
Thanks to Darwin, the world is full of people who think that evolution, in nature, works by: natural selection, or the survival of the fittest. I thought this until I read “Good Enough: The Tolerance for Mediocrity in Nature and Society” by Daniel Milo.
Milo makes a very convincing case that nature actually works by: natural elimination, or the survival of the good enough.
Why might Darwin have gone with natural selection in his book, On the Origin of Species? Milo makes the point that the only real evidence that Darwin had to work with was artificial selection, that is the breeding of farm animals and domestic pets to select for traits that humans found desirable. Darwin’s visit to the Galápagos islands triggered a way of thinking, it did not provide him with the evidence he needed; Darwin’s Finches have become a commonly cited example of natural selection at work, but while Darwin made the observations it was not until 80 years later that somebody else spotted their relevance.
The Origin of Species, or to use its full title: “On the Origin of Species by means of natural selection, or the preservation of favored races in the struggle for life.” is full of examples and terminology relating to artificial selection.
Natural selection, or natural elimination, isn’t the result the same?
Natural selection implies an optimization process, e.g., breeders selecting for a strain of cows that produce the most milk.
Natural elimination is a good enough process, i.e., a creature needs a collection of traits that are good enough for them to create the next generation.
A long-standing problem with natural selection is that it fails to explain the diversity present in a natural population of some breed of animal (there is very little diversity in each breed of farm animal, they have been optimized for consistency). Diversity is not a problem for natural elimination, which does not reduce differences in its search for fitness.
The diversity produced as a consequence of natural elimination creates a population containing many neutral traits (i.e., characteristics that have no positive or negative impact on continuing survival). When a significant change in the environment occurs, one or more of the neutral traits may suddenly have positive or negative survival consequences; the creatures with the positive traits have opportunity time to adapt to the changed environment. A population whose members possess a diverse range of neutral traits has a higher chance of long-term survival than a population where diversity has been squeezed in the quest for the fittest.
I think that natural elimination also applies within software ecosystems. Commercial products survive if enough customers buy them, software developers need good enough know-how to get the job done.
I’m sure customers would prefer software ecosystems to operate on the principle of survival of the fittest (it reduces their costs). Over the long term is society best served by diverse software ecosystems or softwaremonocultures? Diversity is a way of encouraging competition, but over time there is diminishing returns on the improvements.
Recent Comments