Archive
Searching for inaccurate literals in R
In creating the numbers tool I wanted to be able to do two things, 1) obtain information about what source did by matching the numeric literals it contained against a database of ‘interesting’ values (now with over 14,000 entries) and 2) flag possible incorrect numeric literals (e.g., 3.1459265 when 3.14159265 had been intended in core/Helix.cpp of the MIFit source {now fixed}).
I have recently been enhancing ‘incorrect numeric literal’ support and using the latest release of R as a test bed (whose floating-point literals are almost identical to the last release I looked at, R-2.11.1, log file here).
The first fault I found (0.20403... instead of 0.020403...) looked very serious until I realised it was involved in calculating an initial value feed into an iterative algorithm (at worst causing an extra iteration or so). It looks like the developer overlooked the “e-1” that appears in the original (click on ‘Page 48’).
The second possible problem turned out to be an ambiguity in the file main/color.c which contains the comment “CIE-XYZ to sRGB” above three expressions that perform a conversion from CIE-XYZ to BT.709 RGB. Did the developer get the comment or the numeric literals wrong? People are known to confuse the two forms of RGB (for an explanation see Annex B) .
Apart from a few minor errors such as 0.950301 instead of 0.9503041 (in …/grDevices/R/postscript.R) nothing else of interest turned up so I shifted attention to the add-on packages available on the Comprehensive R Archive Network.
The 3,000+ packages occupy almost 2 Gig in compressed form (fortunately numbers can operate directly on compressed archives and the files did not need to be unpacked) and I decided to limit the analysis to just the R source files, which cut the number of floating-point literals down to around 2 million (after ignoring the contents of comments, 10M compressed log file here).
The various floating-point literals having a value close to 2.30258509299404568402 (the most common match; no idea why the value ln(10) or 1/log(e) should be so popular) highlight the various issues that crop up when using approximate matching to look for faults. The following are some of these matches (first number is total occurrences, second sequence is the literal appearing in the source with dot denoting the same digit as in the number matched against):
92 ........ 2.30258509299404568402 ln(10) or 1/log(e) 5 ...............5 2.30258509299404568402 ln(10) or 1/log(e) 1 .....80528052805 2.30258509299404568402 ln(10) or 1/log(e) 3 .....6 2.30258509299404568402 ln(10) or 1/log(e) 2 .....67 2.30258509299404568402 ln(10) or 1/log(e) 1 .....38 2.30258509299404568402 ln(10) or 1/log(e) 2 .....8 2.30258509299404568402 ln(10) or 1/log(e) 1 .....42 2.30258509299404568402 ln(10) or 1/log(e) 2 ......7 2.30258509299404568402 ln(10) or 1/log(e) 2 ......2 2.30258509299404568402 ln(10) or 1/log(e) 1 ....... 2.30258509299404568402 ln(10) or 1/log(e) 2 .....6553 2.30258509299404568402 ln(10) or 1/log(e) 1 .......4566 2.30258509299404568402 ln(10) or 1/log(e)
Most of those 92 seven digit matches occur in a subdirectory called data implying that they do not occur within code expressions, while .....80528052805 contains enough extra trailing non-matching digits to suggest a different value really was intended. Are there enough unmatched trailing digits in .....6553 to consider it a different value? More experience needs to be gained before attempting to make this call automatically.
At the moment a person has to look at the code containing these ‘close’ values to decide whether the author made a mistake or really did mean to use the value given (unfortunately numbers does not yet have a fancy gui to simplify this task). Sometimes the literals appear in data and other times in an expression that requires domain knowledge to figure out whether it is correct or not. My cursory sampling of the very large data set did not find any serious problems.
Some of the unmatched literals contain so few significant digits they would match many entries in a database of ‘interesting’ values. For instance the numbers database used to contain 745.0, the mean radius of the minor planet Sedna (according to the latest NASA data), but it was removed because of the large number of false positive matches it generated.
Many of the unmatched literals appear to do not appear to have any special interest outside of code that contains them, for instance 0.2.
I am hoping that readers of this blog will download numbers and run their code through it. They might find some faults in their code and add new values to their local ‘interesting’ numbers database to target their own application domain(not forgetting to email me a copy to include in the next release). Suggestions for improving the detection of inaccurate literals always welcome (check to the TODO file first).
An interesting observation from comparing the mathematical equations in the book Computation of Special Functions with the Fortran source provided by its authors is that when a ‘known’ constant (e.g., pi, pi/2) appears in isolation (e.g., as an argument or a value in an assignment) its literal representation often contains as many digits as supported in 64-bits, while when the same constant appears within an expression evaluating a polynomial it often contains the same number of digits as the other literals appearing in that expression (which is usually less than supported in 64-bits).
Using evolution to reduce competition
The Microsoft purchase of Skype got me thinking back to my time as an advisor to the Monitoring Trustee appointed by the European Commission in the EU/Microsoft competition court case. The Commission wanted to introduce competition into the Windows Work Group server market and it hoped that by requiring Microsoft to license all of the necessary communication protocols companies would produce products that were plug-compatible with Microsoft products. The major flaw in this plan turned out to be economics, we estimated it would cost around £100 million to implement the protocols and making a worthwhile profit on this investment looked decidedly problematic.
Microsoft’s approach to publishing protocol specifications went through three stages: 1) doing everything they could not to do it, 2) following the judgment handed down by the court, 3) actively documenting additional protocols and making all the documents publicly available. Yes, as the documentation process progressed Microsoft started to see the benefits of having English prose documentation (previously the documentation was the source code) but I suspect the switch from (2) to (3) was made possible by the economic analysis that implied there would not be any competition in the server market.
Skype have not made their client/server protocols public, will Microsoft do so? I suspect not because there is no benefit for them to do so. Also I’m sure that Microsoft will want to steer clear of antitrust authorities and will not be making Skype an integral part of Windows’ internal functionality.
What progress has been made in reverse engineering the Skype protocols? There is a community of people trying to figure them out but they have not made the progress that enabled Andrew Tridgell to quickly get something useful up and running that could then evolve into a full blown implementation of a Microsoft protocol.
What lesson can Skype product managers learn from the Microsoft experience of having to make their proprietary protocols available to third parties? I don’t think Microsoft intentionally did any the following:
- Don’t write any English prose documentation; ensure that the source code is the only specification of the protocols. This will make it easier for point 3) to occur,
- proprietary protocols are your friend, even designing ‘better’ alternatives to non-proprietary protocols,
- don’t put too much of a brake on evolution, i.e., allow developers to do what they always want to do which is to make quick fixes to the code and tweak it here and there resulting in a tangle that cannot be simplified. This will significantly drive up third-party costs as they will not be able to create a product handling a useful subset (i.e., they will have to implement everything) and the tangle make sit harder form them to sure that what they have done is correct.
What might be the short term costs of following this strategy? Very good developers are used to learning by reading code (lack of documentation is a fact of life for may of them). Experience has shown that allowing developers to make quick fixes and tweak code often results in difficult to maintain code (ok, so a small group of developers have to be paid above the market rate to ensure access to their code memory). If developers really do dig themselves into a very large hole it is always possible to completely redesign the protocols and provide a very major upgrade (Skype can always reinvent its own protocols, an option not available to third parties which have to follow slavishly behind; this option has always been open to Microsoft with its protocols, i.e., the courts did not place any restrictions on protocol changes).
Where did the £100 million figure come from? The problem of estimating development cost was approached from various angles. The one I used was to estimate the number of requirements at 50,000 (there are 38,158 MUSTs in the first public release of the documents) of which 1,651 occur in the SMB specification for which there is a 450KLOC implementation (i.e., samba source in 2006), giving an estimate of (50000/1651)*450K -> 13.6 MLOC in the final implementation. At £10 per line we get a bit more than £100 million.
Fingerprinting the author of the ZeuS Botnet
The source code of the ZeuS Botnet is now available for download. I imagine there are a few organizations who would like to talk to the author(s) of this code.
All developers have coding habits, that is they usually have a particular way of writing each coding construct. Different developers have different sets of habits and sometimes individual developers have a way of writing some language construct that is rarely used by other developers. Are developer habits sufficiently unique that they can be used to identify individuals from their code? I don’t have enough data to answer that question. Reading through the C++ source of ZeuS I spotted a few unusual usage patterns (I don’t know enough about common usage patterns in PHP to say much about this source) which readers might like to look for in code they encounter, perhaps putting name to the author of this code.
The source is written in C++ (32.5 KLOC of client source) and PHP (7.5KLOC of server source) and is of high quality (the C++ code could do with more comments, say to the level given in the PHP code), many companies could increase the quality of their code by following the coding standard that this author seems to be following. The source is well laid out and there are plenty of meaningful variable names.
So what can we tell about the person(s) who wrote this code?
- There is one author; this is based on consistent usage patterns and nothing jumping out at me as being sufficiently different that it could be written by somebody else,
- The author is fluent in English; based on the fact that I did not spot any identifiers spelled using unusual word combinations that often occur when a developer has a poor grasp of English. Update 16-May: skier.su spotted four instances of the debug message “Request sended.” which suggests the author is not as fluent as I first thought.
- The usage that jumped out at me the most is:
for(;; p++)if(*p == '\\' || *p == '/' || *p == 0) { ...
This is taking to an extreme the idea that if a ‘control header’ has a single statement associated with it, then they both appear on the same line; this usage commonly occurs with if-statements and this for/while-statement usage is very rare (this usage also occurs in the PHP code),
- The usage of
true/falsein conditionals is similar to that of newbie developers, for instance writing:return CWA(kernel32, RemoveDirectoryW)(path) == FALSE ? false : true; // and return CWA(shlwapi, PathCombineW)(dest, dir, p) == NULL ? false : true; // also return CWA(kernel32, DeleteFileW)(file) ? true : false;
in a function returning
boolinstead of:return CWA(kernel32, RemoveDirectoryW)(path); //and return CWA(shlwapi, PathCombineW)(dest, dir, p) != NULL // and return CWA(kernel32, DeleteFileW)(file);
The author is not a newbie developer, perhaps sometime in the past they were badly bitten by a Microsoft C++ compiler bug, found that this usage worked around the problem and have used it ever since,
- The author vertically aligns the assignment operator in statement sequences but not in a sequence of definitions containing an initializer:
// = not vertically aligned here DWORD itemMask = curItem->flags & ITEMF_IS_MASK; ITEM *cloneOfItem = curItem; // but is vertically aligned here: desiredAccess |= GENERIC_WRITE; creationDisposition = OPEN_ALWAYS;
Vertical alignment is not common and I would have said that alignment was more often seen in definitions than statements, the reverse of what is seen in this code,
- Non-terminating loops are created using
for(;;)rather than the more commonly seenwhile(TRUE), - The author is happy to use
gototo jump to the end of a function, not a rare habit but lots of developers have been taught that such usage is bad practice (I would say it depends, but that discussion belongs in another post), - Unnecessary casts often appear on negative constants (unnecessary in the sense that the compiler is required to implicitly do the conversion). This could be another instance of a previous Microsoft compiler bug causing a developer to adopt a coding habit to work around the problem.
Could the source have been processed by an code formatter to remove fingerprint information? I think not. There are small inconsistencies in layout here and there that suggest human error, also automatic layout tends to have a ‘template’ look to it that this code does not have.
Update 16 May: One source file stands out as being the only one that does not make extensive use of camelCase and a quick search finds that it is derived from the ucl compression library.
Unused function parameters
I have started redoing the source code measurements that appear in my C book, this time using a lot more source, upgraded versions of existing tools, plus some new tools such as Coccinelle and R. The intent is to make the code and data available in a form that is easy for others to use (I am hoping that one or more people will measure the same constructs in other languages) and to make some attempt at teasing out relationships in the data (previously the data was simply plotted with little or no explanation).
While it might be possible to write a paper on every language construct measured, I don’t have the time to do the work. Instead, I will use this blog to make a note of the interesting things that crop up during the analysis of each construct I measure.
First up are unused function parameters (code and data), which at around 11% of all parameters are slightly more common than unused local variables (Figure 190.1). In the following plot black circles are the total number of functions having a given number of parameters, red circles a given number of unused parameters, blue line a linear regression fit of the red circles, and the green line is derived from black circle values using a formula I concocted to fit the data and have no theoretical justification for it.
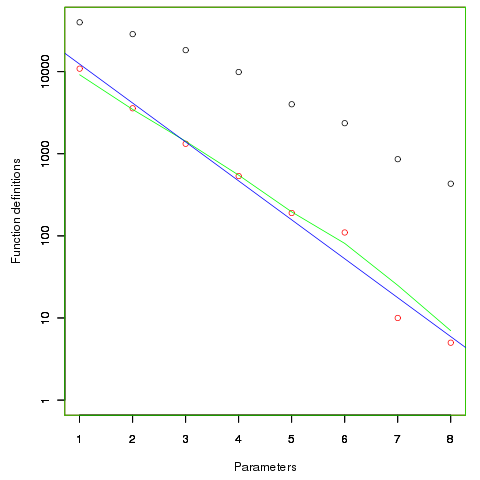
The number of functions containing a given number of unused parameters drops by around a factor of three for each additional unused parameter. Why is this? The formula I came up with for estimating the number of functions containing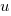 
unused parameters is: 
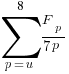, where 
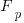is the total number of function definitions containing 
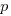parameters.
Which parameter, for those functions defined with more than one, is most likely to be unused? My thinking was that the first parameter might either hold the most basic information (and so rarely be unused) or hold information likely to be superseded when new parameters are added (and so commonly be unused), either way I considered later parameters as often being put there for later use (and therefore more likely to be unused). The following plot is for eight programs plus the sum of them all; for all functions defined with between one and eight parameters, the percentage of times the 
‘th parameter is unused is given. The source measured contained 104,493 function definitions containing more than one parameter with 16,643 of these functions having one or more unused parameter, there were a total of 235,512 parameters with 25,886 parameters being unused.
There is no obvious pattern to which parameters are likely to be unused, although a lot of the time the last parameter is more likely to be unused than the penultimate one.
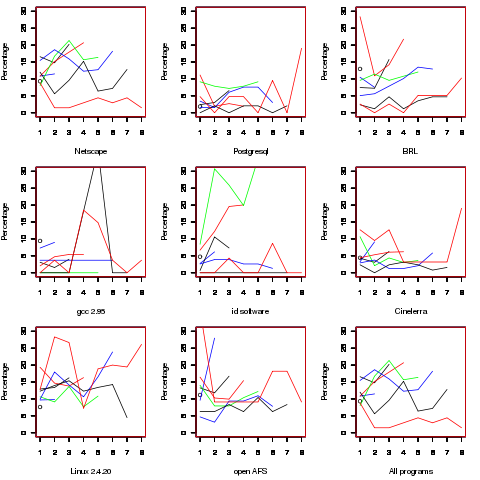
Looking through the raw data I noticed that there seemed to be some clustering of names of unused parameters, in particular if the ‘th parameter was unused in two adjacent ‘unused parameter’ functions they often had the same name. The following plot is for all measured source and gives the percentage of same name occurrences; the matching process analyses function definitions in the order they occur within a source file and having found one unused parameter its name is compared against the corresponding parameter in the next function definition with the same number of parameters and having an unused parameter at the same position.
Before getting too excited about this pattern, we should ask if something similar exists for the used parameters. When I get around to redoing the general parameter measurements, I will look into this question. The numbers of occurrences for functions containing eight parameters is close to minimal.
The functions containing these same-name unused parameters appear to also have related function names. Is this a case of related function being grouped together, often sharing parameter names, and when one of them has an unused parameter the corresponding parameter in the others is also unused?
Is there a correlation between number of parameters and number of statements, are functions containing lots of statements less likely to have unused parameters? What effect does software evolution have (most of this kind of research measures executable code, not variable definitions)?
Estimating the quality of a compiler implemented in mathematics
How can you tell if a language implementation done using mathematical methods lives up to the claims being made about it, without doing lots of work? Answers to the following questions should give you a good idea of the quality of the implementation, from a language specification perspective, at least for C.
- How long did it take you to write it? I have yet to see any full implementation of a major language done in less than a man year; just understanding and handling the semantics, plus writing the test cases will take this long. I would expect an answer of at least several man years
- Which professional validation suites have you tested the implementation against? Many man years of work have gone into the Perennial and PlumHall C validation suites and correctly processing either of them is a non-trivial task. The gcc test suite is too light-weight to count. The C Model Implementation passed both
- How many faults have you found in the C Standard that have been accepted by WG14 (DRs for C90 and C99)? Everybody I know who has created a full implementation of a C front end based on the text of the C Standard has found faults in the existing wording. Creating a high quality formal definition requires great attention to detail and it is to be expected that some ambiguities/inconsistencies will be found in the Standard. C Model Implementation project discoveries include these and these.
- How many ‘rules’ does the implementation contain? For the C Model Implementation (originally written in Pascal and then translated to C) every if-statement it contained was cross referenced to either a requirement in the C90 standard or to an internal documentation reference; there were 1,327 references to the Environment and Language clauses (200 of which were in the preprocessor and 187 involved syntax). My C99 book lists 2,043 sentences in the equivalent clauses, consistent with a 70% increase in page count over C90. The page count for C1X is around 10% greater than C99. So for a formal definition of C99 or C1X we are looking for at around 2,000 language specific ‘rules’ plus others associated with internal housekeeping functions.
- What percentage of the implementation is executed by test cases? How do you know code/mathematics works if it has not been tested? The front end of the C Model Implementation contains 6,900 basic blocks of which 87 are not executed by any test case (98.7% coverage); most of the unexecuted basic blocks require unusual error conditions to occur, e.g., disc full, and we eventually gave up trying to figure out whether a small number of them were dead code or just needed the right form of input (these days genetic programming could be used to help out and also to improve the quality of coverage to something like say MC/DC, but developing on a PC with a 16M hard disc does limit what can be done {the later arrival of a Sun 4 with 32M of RAM was mind blowing}).
Other suggested questions or numbers applicable to other languages most welcome. Some forms of language definition do not include a written specification, which makes any measurement of implementation conformance problematic.
Proving software correct
Users want confidence that software is ‘correct’; what constitutes correct depends on who you talk to and can vary between doing what the user expects and behaving according to a specification (which may include behavior that users did not expect or want).
The gold standard for software correctness is that achieved by mathematical proofs, or at least what most people believe is achieved by such proofs, i.e., a statement that is shown through a sequence of steps to be derived from a set of axioms. The sequence of steps used in most real proofs operate at a much higher level than axioms and rely on the reader to fill in the gaps left between each step. Ever since theorems were first stated they sometimes contained faults, i.e., were not correct theorems, and as mathematicians have continued to increase the size and complexity of theorems being ‘proved’ the technical and social issues involved in believing a published proof have grown in complexity.
Software proofs usually operate by translating the source in to some mathematical formalism and using a theorem prover to show that one or more properties are met. Perhaps the most famous use of such a proof that had an outcome different than that predicted is the 1996 Ariane 5 rocket crash; various proofs had been obtained for the Ariane 4 software showing that the value of some variables would never exceed given limits, these proofs involved input values that depended on the performance of the rocket and because Ariane 5 was more powerful than Ariane 4 the proofs were no longer valid (management would have found this out had they recheck the proofs using the larger values). Update: My only knowledge of this work comes from a conversation I recall with somebody working in the formal verification area, I no longer have contact with them and the company they worked for no longer exists; Pascal Cuoq’s comment below suggests they may have overstated the formal nature of the work, I have no means of double checking.
Purveyors of ‘software proof’ systems will tell you about the importance of feeding in the correct input values and will tell you about the known proofs they have managed to verify using their system. The elephant in the room that rarely gets mentioned is the correctness of the program that translates source code into the mathematical formalism used. These translators often handle that subset of the language which is relatively easy to map to the target formalism, the MALPAS C to IL translator is one exception to this (ok, yes my company wrote this translator so the opinion might be a little biased).
The method commonly associated with claims of correctness proof for a translator or compiler is slightly different from that described above for applications. This method involves manually writing some mathematics, using the chosen formalism, that ‘implements’ the translator/compiler. Strangely there are people who think that doing this is sufficient to claim the compiler is ‘verified’ or ‘proved correct’. As any schoolboy knows it is possible to write mathematics that contains mistakes and the writing of a mathematical implementation is just the first step in a process intended to increase confidence in a claim of correctness.
One of the questions that might be asked of a ‘mathematics implementation’ of a compiler is: does it faithfully interpret source code syntax/semantics according to the syntax/semantics specified in the appropriate language document?
Answering this question requires that the language syntax/semantics be specified in some mathematical notation that is amenable to formal analysis. Various researchers have created mathematical models for languages such as Ada, CHILL and C. However, these models are not recognized as being definitive, that status belongs to the corresponding ISO Standard written in English prose. The Modula-2 standard is specified using both English prose and equivalent mathematical notation with both having equal status as the definition of the language (any inconsistency between the two is decided why analyzing what behavior was intended); there were lots of plans to do stuff with this mathematics but the ISO language committee struggled just to produce a tool capable of printing the mathematics.
The developers of the Compcert system refer to it as a formally verified C compiler front-end when the language actually verified is called Clight, which they describe as a subset of the C language. This is very interesting work and I hope they continue to refine it and add support for more C-like constructs. But let’s be clear, the one thing missing from this project is any proof of a connection to the requirements contained in the C Standard.
I don’t know what it is about formal verification but those involved can at the same time be both very particular about the language they use in their mathematics and completely over the top in the claims they make about what their tools do. A speaker from Polyspace at one MISRA C conference claimed his tool could detect 100% of the coding guidelines specified in MISRA C, a surprising achievement for a runtime tool (as it was then) enforcing requirements mainly aimed at source code; I eventually got him to agree that the tool detected 100% of the constructs specified by the small subset of guidelines they had implemented.
I doubt that the Advertising Standard Authority would allow adverts containing the claims made by some formal verification advocates to appear in print or on TV; if soap manufacturers have to follow ASA rules then so should formal verification researchers.
Without a language specification written in a form amenable to mathematical analysis any claims of correctness have to be based on the traditional means of reading English prose very carefully and writing lots of tests to probe every obscure corner of the language specification. This was the approach used for the production of the Model Implementation of C, a system designed to detect all unspecified, implementation defined and undefined uses in C programs (it used a compiler, linker and interpreter). One measure of how well an implementor has studied the standard is how many faults they have discovered in it (some people claim this is a quality of standard issue, but the similar number of defects reported against the Ada and C Standards show that at least for Ada this is not true); here are some from the Model Implementation project.
Performance on independently written tests can be a good indicator of implementation correctness, depending on the quality of the tests. Both the Perennial and PlumHall C validation suites are of high quality, while suites such as the gcc testsuite are rather ad-hoc, have poor coverage and tend to be runtime oriented. The problem with high quality validation suites is that they cost enough money to put them out of reach of many research groups (I suspect another problem is that such groups don’t understand the benefits of using such suites or think they can do just as good a job in a few weeks).
Recently a new formal verification tool for C has appeared that performs all its verification checking at program runtime, i.e., after the user source has been translated to executable form. It is still very early days for kcc (they have yet to chose a name and the command used to invoke the translator is currently being used), they have an initial system up and running and are keen to continue improving it.
I am interested in the system because of what it might evolve into, including:
- a means of quickly checking the behavior of obscure bits of code (I get asked all sorts of weird questions and my brain is not always willing to switch to C language lawyer mode),
- a means of checking the consistency of the requirements in the C Standard, which will require another tool making use of the formalism built up by kcc,
- a tool which would help developers understand which parts of the C Standard they need to look at to understand some construct (the tool currently has a trace mode that needs lots of work).
Recent Comments