Archive
Program analysis via information leakage
The use of software in high value transactions has created an interesting new field of software research that investigates the leakage of information from programs. The kind of information leaked, so-called sideband information, can take various forms, including:
- The amount of time taken to perform some operation. Many developers instinctively do their best to ensure that code does not take any longer to execute than it has to. In the case of one commonly used authentication system, the time taken to fail to authenticate an encryption key provided useful information on how close one trial encryption-key was compared to another (the closer the trial key to the actual key, the longer the authentication took to fail). The obvious implementation technique to foil this kind of attack is to add random delays into the authentication process.
It has even proved possible to perform timing attacks against a remote machine over the Internet to remote
- Use of some part of the value of secure information, by a system library function, to create the value passed back to the caller, e.g.,
if (secret_value & 0xf000) // Tell the caller that the top 'secret' four bits are set return 1; else return 0;
Researchers have been able to analyse the information flow of input values through some very large C programs.
- Analyse of network traffic routing information to work out who is talking to who. Various kinds of anonymizers have been created in attempt to make various forms of Internet traffic untraceable.
Any Internet program is accessible to information flow analysis. Using these techniques to analyse the search algorithm used by Google might be overly ambitious. A Google algorithm that might be within reach of is the one used by Adwords; the behavior of this algorithm is of interest to a growing number of people.
Information leakage techniques are becoming more widely known and developers working on programs containing a security component now need to consider how they can prevent information being leaked to attackers who sample program behavior looking for exploitable weaknesses.
Variations in the literal representation of Pi
The numbers system I am developing attempts to match numeric literals contained in a file against a database of interesting numbers. One of the things I did to quickly build a reasonably sized database of reliable values was to extract numeric literals from a few well known programs that I thought I could trust.
R is a widely used statistical package, and Maxima is a computer algebra system with a long history. Both contain a great deal of functionality and are actively maintained.
To my surprise, the source code of both packages contain a large variety of different literal values for 
, or to be exact, the number of digits contained in the literals varied by more than I expected. In the following table, the value to the left of the representation is the number of occurrences; values listed in increasing literal order:
Maxima R
2 3.14159
14 3.141592
1 3.1415926
1 3.14159265 2 3.14159265
3 3.1415926535
4 3.14159265358979
14 3.141592653589793
3 3.1415926535897932385 3 3.1415926535897932385
9 3.14159265358979324
1 3.14159265359
1 3.1415927
1 3.141593
The comments in the Maxima source led me to believe that some thought had gone into ensuring that the numerical routines were robust. Over 3/4 of the literal representations of have a precision comparable to at least that of 64-bit floating-point (I’m assuming an IEEE 754 representation in this post).
In the R source, approximately 2/3 of the literal representations of have a precision comparable to that of 32-bit floating-point.
Closer examination of the source suggests one reason for this difference. Both packages make heavy use of existing code (translated from Fortran to Lisp for Maxima and from Fortran to C for R); using existing code makes good sense and because of its use in scientific and engineering applications many numerical libraries have been written in Fortran. Maxima has adapted the slatec library, whereas the R developers have used a variety of different libraries (e.g., specfun).
How important is variation in the representation of Pi?
- A calculation based on a literal that is only accurate to 32-bits is likely to be limited to that level of accuracy (unless errors cancel out somewhere).
- Inconsistencies in the value used to represent Pi are a source of error. These inconsistencies may be implicit, for instance literals used to denote a value derived from such as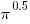
often seem to be based on more precise values of Pi than appear in the code.
The obvious solution to this representation issue of creating a file containing definitions of all the frequently used literal values has possible drawbacks. For instance, numerical accuracy is a strange beast, and increasing the precision of one literal without doing the same for other literals appearing in a calculation can sometimes reduce the accuracy of the final result.
Pulling together existing libraries to build a package is often very cost-effective, but numerical accuracy is a slippery beast, and this inconsistent usage of literals suggests that developers from these two communities have not addressed the system level consequences of software reuse.
Update 6 April: After further rummaging around in the R source distribution, I found that things are not as bad as they first appear. Only two of the single precision instances of listed above occur in the C or Fortran source code, the rest appear in support files (e.g., m4 scripts and R examples).
Recent Comments