Archive
Design of the Whetstone benchmark
The Whetstone benchmark was once a widely cited measure of computer performance. This benchmark consisted of a single program, originally designed for Algol 60 based applications, and later translated to other languages (over 85% of published results used Fortran). The source used as representative of typical user programs came from scientific applications, which has some characteristics that are very non-representative of non-scientific applications, e.g., use of floating-point, and proportionally more multiplications and multidimensional array accesses. Dhrystone benchmark was later designed with the intent of being representative of a broader range of applications.
While rooting around for Whetstone result data, I discovered the book Algol 60 Compilation and Assessment by Brian Wichmann. Despite knowing Brian for 25 years and being very familiar with his work on compiler validation, I had never heard of this book (Knuth’s An Empirical Study of Fortran Programs has sucked up all the oxygen in this niche).
As expected, this 1973 book has a very 1960s model of cpu/compiler behavior, much the same as MIX, the idealised computer used by Knuth for the first 30-years of The Art of Computer Programming.
The Whetstone world view is of a WYSIWYG compiler (i.e., each source statement maps to the obvious machine code), and cpu instructions that always take the same number of clock cycles to execute (the cpu/memory performance ratio had not yet moved far from unity, for many machines).
Compiler optimization is all about trying not to generate code, and special casing to eke out many small savings; post-1970 compilers tried hard not to be WYSIWYG. Showing compiler correctness is much simplified by WYSIWIG code generation.
Today, there are application domains where the 1960s machine model still holds. Low power embedded systems may have cpu/memory performance ratios close to unity, and predictable instruction execution times (estimating worst-case execution time is a minor research field).
Creating a representative usage-based benchmark requires detailed runtime data on what the chosen representative programs are doing. Brian modified the Whetstone Algol interpreter to count how many times each virtual machine op-code was executed (see the report Some Statistics from ALGOL Programs for more information).
The modified Algol interpreter was installed on the KDF9 at the National Physical Laboratory and Oxford University, in the late 1960s. Data from 949 programs was collected; the average number of operations per program was 152,000.
The op-codes need to be mapped to Algol statements, to create a benchmark program whose compiled form executes the appropriate proportion of op-codes. Some op-code sequences map directly to statements, e.g., Ld addrof x, Ld value y, Store, maps to the statement: x:=y;.
Counts of occurrences of each language construct in the source of the representative programs provides lots of information about the proportions of the basic building blocks. It’s ‘just’ a matter of sorting out the loop counts.
For me, the most interesting part of the book is chapter 2, which attempts to measure the execution time of 40+ different statements running on 36 different machines. The timing model is 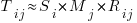 , where
, where 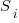 is the
is the 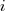 ‘th statement,
‘th statement, 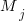 is the
is the 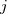 ‘th machine,
‘th machine, 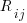 an adjustment factor intended to be as close to one as possible, and
an adjustment factor intended to be as close to one as possible, and 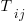 is execution time. The book lists some of the practical issues with this model, from the analysis of timing data from current machines, e.g., the impact of different compilers, and particular architecture features having a big performance impact on some kinds of statements.
is execution time. The book lists some of the practical issues with this model, from the analysis of timing data from current machines, e.g., the impact of different compilers, and particular architecture features having a big performance impact on some kinds of statements.
The table below shows statement execution time, in microseconds, for the corresponding computer and statement (* indicates an estimate; the book contains timings on 36 systems):
ATLAS MU5 1906A RRE Algol 68 B5500 Statement 6.0 0.52 1.4 14.0 12.1 x:=1.0 6.0 0.52 1.3 54.0 8.1 x:=1 6.0 0.52 1.4 *12.6 11.6 x:=y 9.0 0.62 2.0 23.0 18.8 x:=y + z 12.0 0.82 3.2 39.0 50.0 x:=y × z 18.0 2.02 7.2 71.0 32.5 x:=y/z 9.0 0.52 1.0 8.0 8.1 k:=1 18.0 0.52 0.9 121.0 25.0 k:=1.0 12.0 0.62 2.5 13.0 18.8 k:=l + m 15.0 1.07 4.9 75.0 35.0 k:=l × m 48.0 1.66 6.7 45.0 34.6 k:=l ÷ m 9.0 0.52 1.9 8.0 11.6 k:=l 6.0 0.72 3.1 44.0 11.8 x:=l 18.0 0.72 8.0 122.0 26.1 l:=y 39.0 0.82 20.3 180.0 46.6 x:=y ^ 2 48.0 1.12 23.0 213.0 85.0 x:=y ^ 3 120.0 10.60 55.0 978.0 1760.0 x:=y ^ z 21.0 0.72 1.8 22.0 24.0 e1[1]:=1 27.0 1.37 1.9 54.0 42.8 e1[1, 1]:=1 33.0 2.02 1.9 106.0 66.6 e1[1, 1, 1]:=1 15.0 0.72 2.4 22.0 23.5 l:=e1[1] 45.0 1.74 0.4 52.0 22.3 begin real a; end 96.0 2.14 80.0 242.0 2870.0 begin array a[1:1]; end 96.0 2.14 86.0 232.0 2870.0 begin array a[1:500]; end 156.0 2.96 106.0 352.0 8430.0 begin array a[1:1, 1:1]; end 216.0 3.46 124.0 452.0 13000.0 begin array a[1:1, 1:1, 1:1]; end 42.0 1.56 3.5 16.0 31.5 begin goto abcd; abcd : end 129.0 2.08 9.4 62.0 98.3 begin switch s:=q; goto s[1]; q : end 210.0 24.60 73.0 692.0 598.0 x:=sin(y) 222.0 25.00 73.0 462.0 758.0 x:=cos(y) 84.0 *0.58 17.3 22.0 14.0 x:=abs(y) 270.0 *10.20 71.0 562.0 740.0 x:=exp(y) 261.0 *7.30 24.7 462.0 808.0 x:=ln(y) 246.0 *6.77 73.0 432.0 605.0 x:=sqrt(y) 272.0 *12.90 91.0 622.0 841.0 x:=arctan(y) 99.0 *1.38 18.7 72.0 37.5 x:=sign(y) 99.0 *2.70 24.7 152.0 41.1 x:=entier(y) 54.0 2.18 43.0 72.0 31.0 p0 69.0 *6.61 57.0 92.0 39.0 p1(x) 75.0 *8.28 65.0 132.0 45.0 p2(x, y) 93.0 *9.75 71.0 162.0 53.0 p2(x, y, z) 57.0 *0.92 8.6 17.0 38.5 loop time |
The performance studies found wide disparities between expected and observed timings. Chapter 9 does a deep dive on six Algol compilers.
A lot of work and idealism went into gather the data for this book (36 systems!). Unfortunately, the computer performance model was already noticeably inaccurate, and advances in compiler optimization and cpu design meant that the accuracy was only going to get worse. Anyways, there is lots of interesting performance data on 1960 era computers.
Whetstone lived on into the 1990s, when the SPEC benchmark started to its rise to benchmark dominance.
Recent Comments