Archive
Stochastic rounding reemerges
Just like integer types, floating-point types are capable of representing a finite number of numeric values. An important difference between integer and floating types is that the result of arithmetic and relational operations using integer types is exactly representable in an integer type (provided they don’t overflow), while the result of arithmetic operations using floating types may not be exactly representable in the corresponding floating type.
When the result of a floating-point operation cannot be exactly represented, it is rounded to a value that can be represented. Rounding modes include: round to nearest (the default for IEEE-754), round towards zero (i.e., truncated), round up (i.e., towards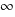 
), round down (i.e., towards 
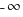), and round to even. The following is an example of round to nearest:
123456.7 = 1.234567 × 10^5
101.7654 = 0.001017654 × 10^5
Adding
= 1.235584654 × 10^5
Round to nearest
= 1.235585 × 10^5 |
There is another round mode, one implemented in the 1950s, which faded away but could now be making a comeback: Stochastic rounding. As the name suggests, every round up/down decision is randomly chosen; a Google patent makes some claims about where the entropy needed for randomness can be obtained, and Nvidia also make some patent claims).
From the developer perspective, stochastic rounding has a very surprising behavior, which is not present in the other IEEE rounding modes; stochastic rounding is not monotonic. For instance: z < x+y does not imply that 0<(x+y)-z, because x+y may be close enough to z to have a 50% chance of being rounded to one of z or the next representable value greater than z, and in the comparison against zero the rounded value of (x+y) has an uncorrelated probability of being equal to z (rather than the next representable greater value).
For some problems, stochastic rounding avoids undesirable behaviors that can occur when round to nearest is used. For instance, round to nearest can produce correlated rounding errors that cause systematic error growth (by definition, stochastic rounding is uncorrelated); a behavior that has long been known to occur when numerically solving differential equations. The benefits of stochastic rounding are obtained for calculations involving long chains of calculations; the rounding error of the result of 
operations is guaranteed to be proportional to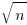 
, i.e., just like a 1-D random walk, which is not guaranteed for round to nearest.
While stochastic rounding has been supported by some software packages for a while, commercial hardware support is still rare, with Graphcore's Intelligence Processing Unit being one. There are some research chips supporting stochastic rounding, e.g., Intel's Loihi.
What applications, other than solving differential equations, involve many long chain calculations?
Training of machine learning models can consume many cpu hours/days; the calculation chains just go on and on.
Machine learning is considered to be a big enough market for hardware vendors to support half-precision floating-point. The performance advantages of half-precision floating-point are large enough to attract developers to reworking code to make use of them.
Is the accuracy advantage of stochastic rounding a big enough selling point that hardware vendors will provide the support needed to attract a critical mass of developers willing to rework their code to take advantage of improved accuracy?
It's possible that the intrinsically fuzzy nature of many machine learning applications swamps the accuracy advantage that stochastic rounding can have over round to nearest, out-weighing the costs of supporting it.
The ecosystem of machine learning based applications is still evolving rapidly, and we will have to wait and see whether stochastic rounding becomes widely used.
Superoptimizers are back in vogue
There has always been the need for a few developers with in-depth knowledge of a particular cpu architecture to sit down and think very hard about how best to implement a snippet of code performing some operation in assembly language, e.g., library implementors wanting the tightest code for a critical inner loop or compiler writers who need to map from intermediate code to machine code.
In 1987 Massalin published his now famous paper that introduced the term Superoptimizer; a program that enumerates all possible combinations of instruction sequences until the shortest/fastest one producing the desired output from the given input is found (various heuristics were used to prune the search space e.g., only considering 15 or so opcodes, and the longest sequence it ever generated contained 12 instructions).
While the idea was widely talked about, it never caught on in practice (a special purpose branch eliminator was produced for GCC; Hacker’s Delight also includes a stand-alone system). Perhaps the guild of mindbogglingly-obtuse-but-fast-instruction-sequences black-balled it (apprentices have to spend several years doing nothing but writing assembly code for their chosen architecture, thinking about how to make it go faster and/or be shorter and only talk to other apprentices/members and communicate with non-converts exclusively about their latest neat sequence), or perhaps it was just a case of not invented here (writing machine code used to be something that even run-of-the-mill developers got to do every now and again), or perhaps it was not considered cost-effective to build a superoptimizer for a given project (I don’t know of anyone offering a generic tool that could be tailored for specific cases) or perhaps developers were happy to just ride the wave of continually faster processors.
It was not until 2008 with Bansal’s thesis that superoptimizer research started to take off (as in paper publication rate increased from once every five years to more than one a year). Bansal found a new market, binary translation i.e., translating the binary of a program built to run on one kind of cpu to run on a different kind of cpu, for instance the Mac 68K emulator.
Bansal and other researchers’ work was oriented towards relatively short instruction sequences. To be really useful, some way of handling longer sequences was needed.
A few days ago Stochastic Superoptimization arrived on the scene (or rather a paper describing it became available for download). Schkufza, Sharma and Aiken use Markov chain Monte Carlo methods to sample the possible instruction sequences rather than generating all of them. The paper gives a 116 instruction example from which the author’s tool removed 16 lines to produce code that went 1.6 times faster (only 30 ‘core’ instructions were given in paper); what is also very interesting is that the tool operates on compiler generated output (gcc/llvm), suggesting the usage build program, profile it and then stochastic superoptimize the hot spots.
Markov chains and Monte Carlo methods are trendy topics that researchers like to write about, so we will certainly see more papers in this area.
These days few developers have had hands-on experience with machine code, so the depth of expertise that was once easy to find is now rare, processors have many more weird and wonderful instructions often interacting with older instructions in obscure ways, and the cpu architecture landscape continues to change regularly. The time may have arrived for superoptimizers to be widely used by industry.
Of course, superoptimizers can work at any level of abstraction, including expression trees built directly from some complicated floating-point calculation that needs to be optimized for accuracy or speed.
Recent Comments