Archive
Distribution of program sizes
Program size, in lines of code (LOC), used to be a topic of conversation among developers and managers. Program size is an issue when computer memory is measured in kilobytes. Large programs would be organized into overlays such that only small subsets needed to be held in memory at any time, i.e., programmer defined memory management.
Management used program size as a proxy for implementation effort/cost. Because size was a topic of conversation, it was possible to ask around to obtain a selection of values for the size of programs with similar functionality (accurate actual implementation costs were/are rarely available via the grapevine, but developers were/are always happy to talk about how small/large their programs were/are). These days, estimating LOC prior to implementation may appear more scientific, but I doubt it’s more accurate.
Once computers containing megabytes of memory became widespread, and the use of third-party libraries continued to grow, program size became a niche topic of conversation.
The size of some operating systems has become an occasional topic of conversation; it wasn’t previously because mainframe/mini computer manufacturers didn’t want customers talking about how much of their expensive memory was taken up by the OS. The size of Microsoft Windows leaked out and the Linux kernel is a topic of research.
Discussions around size have moved on from individual programs to the amount of space taken up by an installed application suite. Today, program size can be a rounding error compared to data files, extensions and add-ons.
Researchers have also moved on; repository size, in LOC/packages, is what now gets reported.
For those who are interested in program size; what is the distribution of program sizes? How many LOC are needed for a program to be above 50%, or in the top 95%?
Recent data on the size of individual programs is surprisingly hard to find, given how often LOC values appear in print. The one dataset I found is from the paper Empirical analysis of the relationship between CC and SLOC in a large corpus of Java methods and C functions, which is derived from the 2010’ish Sourcerer corpus of 13,103 Java projects (each of which I assume contains one program). The plot below shows the LOC (red) and methods (blue/green) for each program, in ascending order, along with values at various percentage points (code+data):
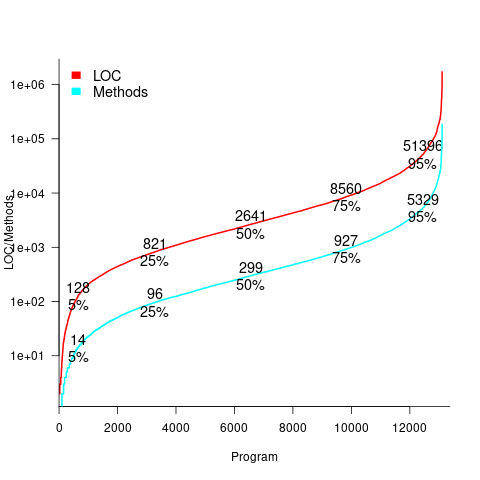
The size of Java programs is very likely to have increased since 2010. How much have grown? I don’t know.
What about the size of programs written in other languages?
I expect Python program size to be smaller, because the huge number of available package removes the need to implement a myriad of boilerplate functionality.
I expect C program size to be larger, both because of the smaller library ecosystem and because C programs tend to be older (programs rarely shrink with age).
Some data on the size of Cobol programs/paragraphs
Before the internet took off in the 1990s, COBOL was the most popular language, measured in lines of code in production use. People who program in Cobol often have a strong business focus, and don’t hang out on sites used aggregated by surveys of programming language use; use of the language is almost completely invisible to those outside the traditional data processing community. So who knows how popular Cobol is today.
Despite the enormous quantity of Cobol code that has been written, very little Cobol source is publicly available (Open source or otherwise; the NIST compiler validation suite is not representative). The reason for the sparsity of source code is that Cobol programs are used to process business data, and the code is useless without the appropriate data (even with the data, the output is only likely to be of interest to a handful of people).
Program and function/method size (in LOC) are basic units of source code measurement. Until open source happened, published papers containing these measurements were based on small sample sizes and the languages covered was somewhat spotty. Cobol oriented research usually has a business orientation, rather than being programming oriented, and now there is a plentiful supply of source code written in non-Cobol languages.
I recently discovered appendix B of 1st Lt Richard E. Boone’s Master’s thesis An investigation into the use of software product metrics for COBOL systems (it’s post Rome period). Several days/awk scripts and editor macros later, LOC data for 178 programs containing 2,682 paragraphs containing 53,255 statements is now online (code+data).
A note on terminology: Cobol functions/methods are called paragraphs.
A paragraph is created by attaching a label to the first statement of the paragraph (there are no variables local to a paragraph; all variables are global). The statement PERFORM NAME-OF-PARAGRAPH ‘calls’ the paragraph labelled by NAME-OF-PARAGRAPH, somewhat like gosub number in BASIC.
It is possible to specify a sequence of paragraphs to be executed, in a PERFORM statement. The statement PERFORM NAME-OF-P1 THRU NAME-OF-P99 causes all paragraphs appearing textually in the code between the start of paragraph NAME-1 and the end of paragraph NAME-99 to be executed.
As far as I can tell, Boone’s measurements are based on individual paragraphs, not any sequences of paragraphs that are PERFORMed (it is likely that some labelled paragraphs are never PERFORMed in isolation).
Appendix B lists for each program: the paragraphs it contains, and for each paragraph the number of statements, McCabe’s complexity, maximum nesting, and Henry and Kafura’s Information flow metric
There are, based on naming, many EXIT paragraphs (711 or 26%); these are single statement paragraphs containing the statement EXIT. When encountered as the last paragraph of a PERFORM THU statement, the EXIT effectively acts like a procedure return statement; in other contexts, the EXIT statement acts like a continue statement.
In the following code the developer could have written PERFORM PARA-1 THRU PARA-4, but if a related paragraph was added between PARA-4 and PARA-END_EXIT all PERFORMs explicitly referencing PARA-4 would need to be checked to see if they needed updating to the new last paragraph.
START. PERFORM PARA-1 THRU PARA-END-EXIT. PARA-1. DISPLAY 'PARA-1'. PARA-2. DISPLAY 'PARA-2'. PARA-3. DISPLAY 'PARA-3'. P3-EXIT. EXIT. PARA-4. DISPLAY 'PARA-4'. PARA-END-EXIT. EXIT. |
The plot below shows the number of paragraphs containing a given number of statements, the red dot shows the count with EXIT paragraphs are ignored (code+data):
How does this distribution compare with that seen in C and Java? The plot below shows the Cobol data (in black, with frequency scaled-up by 1,000) superimposed on the same counts for C and Java (C/Java code+data):
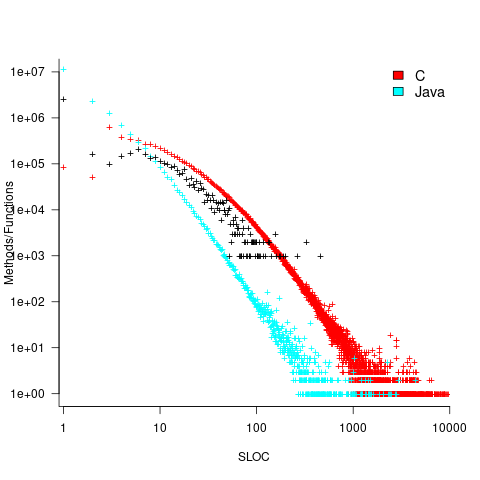
The distribution of statements per paragraph/function distribution for Cobol/C appears to be very similar, at least over the range 10-100. For less than 10-LOC the two languages have very different distributions. Is this behavior particular to the small number of Cobol programs measured? As always, more data is needed.
How many paragraphs does a Cobol program contain? The plot below shows programs ranked by the number of paragraphs they contain, including and excluding EXIT statements (code+data):
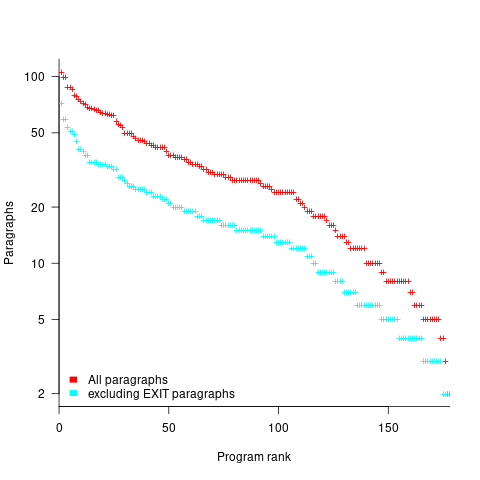
If you squint, it’s possible to imagine two distinct exponential declines, with the switch happening around the 100th program.
It’s tempting to draw some conclusions, but the sample size is too small.
Pointers to large quantities of Cobol source welcome.
Estimating variance when measuring source
Yesterday I finally delivered a paper on if/switch usage measurements to the ACCU magazine editor and today I read about a switch statement usage that, if common, would invalidate a chunk of my results. Does anything jump out at you in the following snippet?
switch (x) { case 1: { z++; ... break; } ... |
Yes, those { } delimiting the case-labeled statement sequence. A quick check of my C source benchmarks showed this usage occurring in around 1% of case-labels. Panic over.
What is the statistical significance, i.e., variance, of that 1%? Have I simply measured an unrepresentative sample, what would be a representative sample and what would be the expected variance within a representative sample?
I am interested in commercial software development, and so I have selected half a dozen or so largish code bases as my source benchmark, preferably written in a commercial environment even if currently available as Open source. I would prefer this benchmark to be an order of magnitude larger, and perhaps I will get around to adding more programs soon.
My if/switch measurements were aimed at finding usage characteristics that varied between the two kinds of selection statements. One characteristic measured was the number of equality tests in the associated controlling expression. For instance, in:
if (x == 1 || x == 2) z--; else if (x == 3) z++; |
the first controlling expression contains two equality tests, and the second one equality test.
Plotting the percentage of equality tests that occur in the controlling expressions of if-if/if-else-if sequences and switch statements, we get the following:
Do these results indicate that if-if/if-else-if sequences and switch statements differ in the number of equality tests contained in their controlling expressions? If I measured a completely different set of source code, would the results be very different?
To answer this question, a probability model is needed. Take as an example, the controlling expressions present in an if-if sequence. If each controlling expression is independent of the others, then the probability of two equality tests, for instance, occurring in any of these expressions is constant and thus given a large sample the distribution of two equality tests in the source has a binomial distribution. The same argument can be applied to other numbers of equality tests and other kinds of sequence.
For each measurement point in the above plot the associated error bars span the square-root of the variance of that point (assuming a binomial distribution, for a normal distribution the length of this span is known as the standard deviation). The error bars overlap, suggesting that the apparent difference in percentage of equality tests in each kind of sequence is not statistically significant.
The existence of some dependency between controlling expression equality tests would invalidate this simply analysis, or at least reduce its reliability. I did notice that in a sequence that containing two equality tests, the controlling expression that contained it tended to appear later in the sequence (the reverse of the example given above). Did I notice this because I tend to write this way? A question for another day.
Recent Comments