The Shape of Code

Just like integer types, floating-point types are capable of representing a finite number of numeric values. An important difference between integer and floating types is that the result of arithmetic and relational operations using integer types is exactly representable in an integer type (provided they don’t overflow), while the result of arithmetic operations using floating types may not be exactly representable in the corresponding floating type.

When the result of a floating-point operation cannot be exactly represented, it is rounded to a value that can be represented. Rounding modes include: round to nearest (the default for IEEE-754), round towards zero (i.e., truncated), round up (i.e., towards 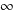), round down (i.e., towards 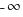), and round to even. The following is an example of round to nearest:

      123456.7    = 1.234567    × 10^5
         101.7654 = 0.001017654 × 10^5
Adding
                  = 1.235584654 × 10^5
Round to nearest
                  = 1.235585    × 10^5

There is another round mode, one implemented in the 1950s, which faded away but could now be making a comeback: Stochastic rounding. As the name suggests, every round up/down decision is randomly chosen; a Google patent makes some claims about where the entropy needed for randomness can be obtained, and Nvidia also make some patent claims).

From the developer perspective, stochastic rounding has a very surprising behavior, which is not present in the other IEEE rounding modes; stochastic rounding is not monotonic. For instance: z < x+y does not imply that 0<(x+y)-z, because x+y may be close enough to z to have a 50% chance of being rounded to one of z or the next representable value greater than z, and in the comparison against zero the rounded value of (x+y) has an uncorrelated probability of being equal to z (rather than the next representable greater value).

For some problems, stochastic rounding avoids undesirable behaviors that can occur when round to nearest is used. For instance, round to nearest can produce correlated rounding errors that cause systematic error growth (by definition, stochastic rounding is uncorrelated); a behavior that has long been known to occur when numerically solving differential equations. The benefits of stochastic rounding are obtained for calculations involving long chains of calculations; the rounding error of the result of operations is guaranteed to be proportional to 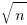, i.e., just like a 1-D random walk, which is not guaranteed for round to nearest.

While stochastic rounding has been supported by some software packages for a while, commercial hardware support is still rare, with Graphcore's Intelligence Processing Unit being one. There are some research chips supporting stochastic rounding, e.g., Intel's Loihi.

What applications, other than solving differential equations, involve many long chain calculations?

Training of machine learning models can consume many cpu hours/days; the calculation chains just go on and on.

Machine learning is considered to be a big enough market for hardware vendors to support half-precision floating-point. The performance advantages of half-precision floating-point are large enough to attract developers to reworking code to make use of them.

Is the accuracy advantage of stochastic rounding a big enough selling point that hardware vendors will provide the support needed to attract a critical mass of developers willing to rework their code to take advantage of improved accuracy?

It's possible that the intrinsically fuzzy nature of many machine learning applications swamps the accuracy advantage that stochastic rounding can have over round to nearest, out-weighing the costs of supporting it.

The ecosystem of machine learning based applications is still evolving rapidly, and we will have to wait and see whether stochastic rounding becomes widely used.