Archive
Analysis of when refactoring becomes cost-effective
In a cost/benefit analysis of deciding when to refactor code, which variables are needed to calculate a good enough result?
This analysis compares the excess time-code of future work against the time-cost of refactoring the code. Refactoring is cost-effective when the reduction in future work time is less than the time spent refactoring. The analysis finds a relationship between work/refactoring time-costs and number of future coding sessions.
Linear, or supra-linear case
Let’s assume that the time needed to write new code grows at a linear, or supra-linear rate, as the amount of code increases (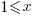
):
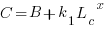
where: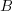 
is the base time for writing new code on a freshly refactored code base, 
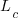is the number of lines of code that have been written since the last refactoring, and 
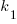and 
are constants to be decided.
The total time spent writing code over 
sessions is:
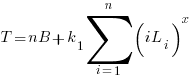
If the same number of new lines is added in every coding session,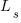 
, and is an integer constant, then the sum has a known closed form, e.g.:
x=1,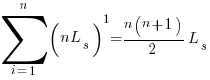 
; x=2,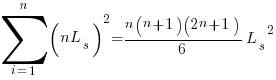 
Let’s assume that the time taken to refactor the code written after sessions is:
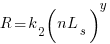
where: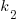 
and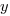 
are constants to be decided.
The reason for refactoring is to reduce the time-cost of subsequent work; if there are no subsequent coding sessions, there is no economic reason to refactor the code. If we assume that after refactoring, the time taken to write new code is reduced to the base cost, 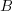, and that we believe that coding will continue at the same rate for at least another 
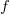sessions, then refactoring existing code after sessions is cost-effective when:
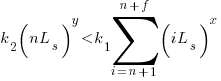
assuming that 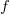is much smaller than , setting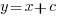 
, and rearranging we get:
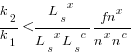
after rearranging we obtain a lower limit on the number of future coding sessions, 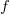, that must be completed for refactoring to be cost-effective after session ::
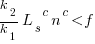
It is expected that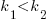 
; the contribution of code size, at the end of every session, in the calculation of 
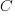and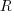 
is equal (i.e., 
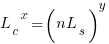), and the overhead of adding new code is very unlikely to be less than refactoring all the newly written code.
With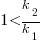 
, 
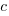must be close to zero; otherwise, the likely relatively large value of 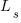(e.g., 100+) would produce surprisingly high values of .
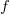Sublinear case
What if the time overhead of writing new code grows at a sublinear rate, as the amount of code increases?
Various attributes have been found to strongly correlate with the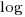 
of lines of code. In this case, the expressions for 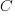and 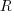become:
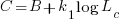
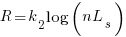
and the cost/benefit relationship becomes:
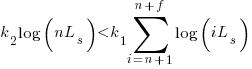
applying Stirling’s approximation and simplifying (see Exact equations for sums at end of post for details) we get:
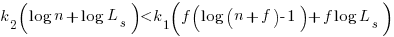
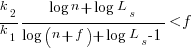
applying the series expansion (for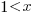 
): 
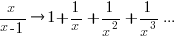, we get
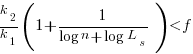
Discussion
What does this analysis of the cost/benefit relationship show that was not obvious (i.e., the relationship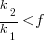 
is obviously true)?
What the analysis shows is that when real-world values are plugged into the full equations, all but two factors have a relatively small impact on the result.
A factor not included in the analysis is that source code has a half-life (i.e., code is deleted during development), and the amount of code existing after sessions is likely to be less than the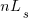 
used in the analysis (see Agile analysis).
As a project nears completion, the likelihood of there being 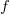more coding sessions decreases; there is also the every present possibility that the project is shutdown.
The values of 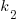and 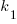encode information on the skill of the developer, the difficulty of writing code in the application domain, and other factors.
Exact equations for sums
The equations for the exact sums, for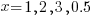 
, are:
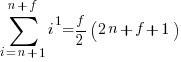
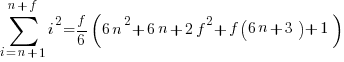
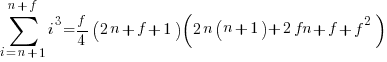
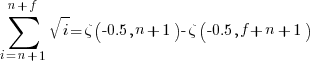, where 
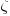is the Hurwitz zeta function.
Sum of a log series: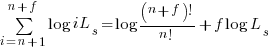 
using Stirling’s approximation we get
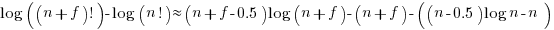
simplifying
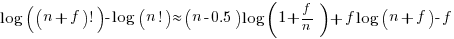
and assuming that 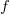is much smaller than gives
Complex software makes economic sense
Economic incentives motivate complexity as the common case for software systems.
When building or maintaining existing software, often the quickest/cheapest approach is to focus on the features/functionality being added, ignoring the existing code as much as possible. Yes, the new code may have some impact on the behavior of the existing code, and as new features/functionality are added it becomes harder and harder to predict the impact of the new code on the behavior of the existing code; in particular, is the existing behavior unchanged.
Software is said to have an attribute known as complexity; what is complexity? Many definitions have been proposed, and it’s not unusual for people to use multiple definitions in a discussion. The widely used measures of software complexity all involve counting various attributes of the source code contained within individual functions/methods (e.g., McCabe cyclomatic complexity, and Halstead); they are all highly correlated with lines of code. For the purpose of this post, the technical details of a definition are glossed over.
Complexity is often given as the reason that software is difficult to understand; difficult in the sense that lots of effort is required to figure out what is going on. Other causes of complexity, such as the domain problem being solved, or the design of the system, usually go unmentioned.
The fact that complexity, as a cause of requiring more effort to understand, has economic benefits is rarely mentioned, e.g., the effort needed to actively use a codebase is a barrier to entry which allows those already familiar with the code to charge higher prices or increases the demand for training courses.
One technique for reducing the complexity of a system is to redesign/rework its implementation, from a system/major component perspective; known as refactoring in the software world.
What benefit is expected to be obtained by investing in refactoring? The expected benefit of investing in redesign/rework is that a reduction in the complexity of a system will reduce the subsequent costs incurred, when adding new features/functionality.
What conditions need to be met to make it worthwhile making an investment, 
, to reduce the complexity, 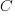, of a software system?
Let’s assume that complexity increases the cost of adding a feature by some multiple (greater than one). The total cost of adding features is:
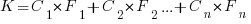
where: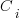 
is the system complexity when feature 
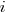is added, and 
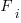is the cost of adding this feature if no complexity is present.
, 
, … 
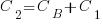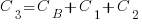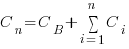
where: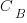 
is the base complexity before adding any new features.
Let’s assume that an investment, , is made to reduce the complexity from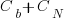 
(with 
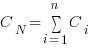) to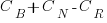 
, where 
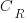is the reduction in the complexity achieved. The minimum condition for this investment to be worthwhile is that:
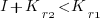or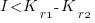 
where: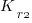 
is the total cost of adding new features to the source code after the investment, and 
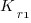is the total cost of adding the same new features to the source code as it existed immediately prior to the investment.
Resetting the feature count back to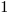 
, we have:
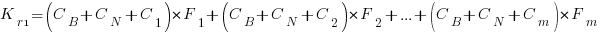
and
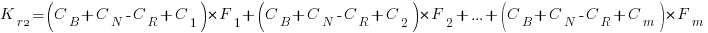
and the above condition becomes:
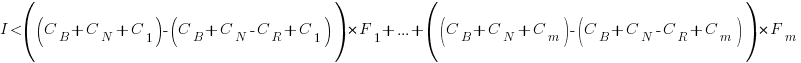
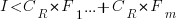
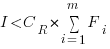
The decision on whether to invest in refactoring boils down to estimating the reduction in complexity likely to be achieved (as measured by effort), and the expected cost of future additions to the system.
Software systems eventually stop being used. If it looks like the software will continue to be used for years to come (software that is actively used will have users who want new features), it may be cost-effective to refactor the code to returning it to a less complex state; rinse and repeat for as long as it appears cost-effective.
Investing in software that is unlikely to be modified again is a waste of money (unless the code is intended to be admired in a book or course notes).
Recent Comments