Archive
Initial impressions of RangeLab
I was rummaging around in the source of R looking for trouble, as one does, when I came across what I believed to be a less than optimally accurate floating-point algorithm (function R_pos_di in src/main/arithemtic.c). Analyzing the accuracy of floating-point code is notoriously difficult and those having the required skills tend to concentrate their efforts on what are considered to be important questions. I recently discovered RangeLab, a tool that seemed to be offering painless floating-point code accuracy analysis; here was an opportunity to try it out.
Installation went as smoothly as newly released personal tools usually do (i.e., some minor manual editing of Makefiles and a couple of tweaks to the source to comment out function calls causing link errors {mpfr_random and mpfr_random2}).
RangeLab works by analyzing the flow of values through a program to produce the set of output values and the error bounds on those values. Input values can be specified as a range, e.g., f = [1.0, 10.0] says f can contain any value between 1.0 and 10.0.
My first RangeLab program mimicked the behavior of the existing code in R_pos_di:
n=-10; f=[1.0, 10.0]; res = 1.0; if n < 0, n = -n; f = 1 / f; end while n ~= 0, if (n / 2)*2 ~= n, res = res * f; end n = n / 2; if n ~= 0, f = f*f; end end |
and told me that the possible range of values of res was:
res ans = float64: [1.000000000000001E-10,1.000000000000000E0] error: [-2.109423746787798E-15,2.109423746787799E-15] |
Changing the code to perform the divide last, rather than first, when the exponent is negative:
n=-10; f=[1.0, 10.0]; res = 1.0; is_neg = 0; if n < 0, n = -n; is_neg = 1 end while n ~= 0, if (n / 2)*2 ~= n, res = res * f end n = n / 2; if n ~= 0, f = f*f end if is_neg == 1, res = 1 / res end end |
and the error in res is now:
res ans = float64: [1.000000000000000E-10,1.000000000000000E0] error: [-1.110223024625156E-16,1.110223024625157E-16] |
Yea! My hunch was correct, moving the divide from first to last reduces the error in the result. I have reported this code as a bug in R and wait to see what the R team think.
Was the analysis really that painless? The Rangelab language is somewhat quirky for no obvious reason (e.g., why use ~= when everybody uses != these days and if conditionals must be followed by a character why not use the colon like Python does?) It would be real useful to be able to cut and paste C/C++/etc and only have to make minor changes.
I get the impression that all the effort went into getting the analysis correct and user interface stuff was a very distant second. This is the right approach to take on a research project. For some software to make the leap from interesting research idea to useful tool it is important to pay some attention to the user interface.
The current release does not deserve to be called 1.0 and unless you have an urgent need I would suggest waiting until the usability has been improved (e.g., error messages give some hint about what is wrong and a rough indication of which line the problem occurs on).
RangeLab has shown that there is simpler method of performing useful floating-point error analysis. With some usability improvements RangeLab would be an essential tool for any developer writing code involving floating-point types.
Update: The R team, in the form of Martin Maechler, resolved my report in just over 14 hours! The function R_pos_di is not called, the pow function from the C library (which takes two double arguments rather than a double and an int) has been found to be more accurate. Martin says this usage is not less accurate even for n=3, which I find surprising; I agree it should be more accurate for large values of n.
pow is one of the more complicated maths functions, involving finding a log, a multiply and then returning the exponent of this result. There are lots of boundary values that need to be checked and the code goes on for a while. I will wait for the usability of RangeLab to improve before attempting to compare its accuracy against the simpler algorithm for integer powers. Looking at the SunOracle library sources, if both arguments have integral values the ‘integer power’ algorithm is used (with the divide performed last).
Learning R as a language
Books written to teach a general purpose programming language are usually organized according to the features of the language and examples often show how a particular language feature is interpreted by a compiler. Books about domain specific languages are usually organized in a way that makes sense in the corresponding application domain and examples usually illustrate how a particular domain problem can be solved using the language.
I have spent a lot of time using R over the last year and by dint of reading lots of R code and various introductions to the language I have managed to piece together a model of the language. I rarely have any trouble learning a general purpose language from its reference manual, but users of domain specific languages are rarely interested in language details and so these reference manuals are usually only intended to be read by people who know the language well (another learning problem is that domain specific languages often contain quirky features rarely seen in other languages; in the case of R I was not lucky enough to know enough other languages to cover all its quirky features).
I managed to one introduction to R written from the perspective of the programming language (and not the application domain): the original The Art of R Programming by Norman Matloff has been expanded and is now available as a book.
Summary. If you know another language and want to quickly learn about the languages features of R I recommend this book. I have not taught raw beginners for over 30 years and have no idea if this book would be of any use to them.
This book does not attempt to teach you to think ‘R’, it is not about the art of R programming. The value of this book is as a single source for a broad coverage of lots of language features explained using lots of examples. Yes, more time could have been spent on the organization and fixing inconsistencies in the layout; these are not show stoppers.
Some people might tell you to buy “Software for Data Analysis” by John Chambers. Don’t; if you are a fan of Finnegans Wake and are nostalgic for the mainframe world of the 1970s you might like to give it a go. (I think Bertrand Meyer’s “Object-oriented Software Construction” is still the best book about the design of a language).
Meanderings. What books are good examples of “The Art of …” writing for domain specific languages? Two that spring to mind are: “Algorithms in Snobol 4” by James Gimpel (still spotted from time to time on second hand book sites) and more recently “SQL For Smarties: Advanced SQL Programming” by Joe Celko.
Yes, I know that R is not really a domain specific language but a language that is primarily used in one domain. Frink is an example of a language containing a major behavior feature that is specific to its intended application domain. I cannot think of any major language feature of R that is specific to statistics.
Halstead’s metrics and flat-Earthers are still with us
I recently discovered a fascinating series of technical reports from the 1970s in the Purdue University e-Pubs archive that shine a surprising light on what are now known as the Halstead metrics.
The first surprises came from Halstead’s A Software Physics Analysis of Akiyama’s Debugging Data; surprising in the size of the data set used (nine measurements of four attributes), the amount of hand waving used to pluck numbers out of thin air, the substantial difference between the counting methods used then and now and the very high correlation found between various measured and calculated attributes.
I disagreed with the numbers Halstead plucked and wrote some R to check Halstead’s results and try out my own numbers. While my numbers significantly changed the effort estimation values, the high correlations between the number of faults and various source attributes remained high. Even changing from the Pearson correlation coefficient (calculating confidence bounds for this coefficient requires that the data be normally distributed, which it is not {program size is now thought to follow a power law/exponential like distribution}) to the Spearman rank correlation coefficient did not have much impact. Halstead seems to have struck luck with this data set.
What did Halstead’s colleagues at Purdue think of these metrics? The report Software Science Revisited: A Critical Analysis of the Theory and Its Empirical Support written four years after Halstead’s flurry of papers contains a lot of background material and points out the lack of any theoretical foundation for some of the equations, that the analysis of the data was weak and that a more thorough analysis suggests theory and data don’t agree. Damming stuff.
If it is known that Halstead’s metrics do not hold up why do writers of books (including Shen, Conte and Dunsmore, the authors of the above report) continue to discuss Halstead’s work? Are they treating this work like Astronomy authors treat Ptolemy’s theory (the Sun and planets revolved around the Earth), i.e., incorrect but part of history and worth a mention?
An observation in the Shen et al report, that Halstead originally proposed the metrics as a way of measuring the complexity of algorithms not programs, explains the background to the report Impurities Found in Algorithm Implementations. Halstead uses the term “impurities” and talks about the need for “purification” in his early work. In this report Halstead points out that the value of metrics for “algorithms written by students” are very different from those for the equivalent programs published in journals and goes on to list eight classes of impurity that need to be purified (i.e., removing or rewriting clumsy, inefficient or duplicate code) in order to obtain results that agree with the theory. Now we know what needs to be done to existing programs to get them to agree with the predictions made by the Halstead metrics!
Did Halstead strike lucky with the data used in his first published analysis of ‘industrial code’, obtaining a very high correlation that caused him to shift focus away from measuring algorithms to measuring programs? Unfortunately, he died soon after publishing the work for which he is now known, so he did not get to comment on how his ideas were used over the subsequent years.
Why are people still attracted to the Halstead metrics, given their poor theoretical foundations and a predictive power that is comparable with using lines of code? Is it because the idea of code volume and length are easy to understand and so are attractive (dimensionally, both of these metrics are the same, a fact that cannot hold for any self-consistent concept of volume and length)? Is it because we don’t have alternative metrics that outperform the poorly performing ones proposed by Halstead, after all Copernicus only won out because his theory gave answers that were more accurate than Ptolomy’s.
Perhaps like the flat Earthers proponents of the Halstead metrics will always be with us.
Searching for inaccurate literals in R
In creating the numbers tool I wanted to be able to do two things, 1) obtain information about what source did by matching the numeric literals it contained against a database of ‘interesting’ values (now with over 14,000 entries) and 2) flag possible incorrect numeric literals (e.g., 3.1459265 when 3.14159265 had been intended in core/Helix.cpp of the MIFit source {now fixed}).
I have recently been enhancing ‘incorrect numeric literal’ support and using the latest release of R as a test bed (whose floating-point literals are almost identical to the last release I looked at, R-2.11.1, log file here).
The first fault I found (0.20403... instead of 0.020403...) looked very serious until I realised it was involved in calculating an initial value feed into an iterative algorithm (at worst causing an extra iteration or so). It looks like the developer overlooked the “e-1” that appears in the original (click on ‘Page 48’).
The second possible problem turned out to be an ambiguity in the file main/color.c which contains the comment “CIE-XYZ to sRGB” above three expressions that perform a conversion from CIE-XYZ to BT.709 RGB. Did the developer get the comment or the numeric literals wrong? People are known to confuse the two forms of RGB (for an explanation see Annex B) .
Apart from a few minor errors such as 0.950301 instead of 0.9503041 (in …/grDevices/R/postscript.R) nothing else of interest turned up so I shifted attention to the add-on packages available on the Comprehensive R Archive Network.
The 3,000+ packages occupy almost 2 Gig in compressed form (fortunately numbers can operate directly on compressed archives and the files did not need to be unpacked) and I decided to limit the analysis to just the R source files, which cut the number of floating-point literals down to around 2 million (after ignoring the contents of comments, 10M compressed log file here).
The various floating-point literals having a value close to 2.30258509299404568402 (the most common match; no idea why the value ln(10) or 1/log(e) should be so popular) highlight the various issues that crop up when using approximate matching to look for faults. The following are some of these matches (first number is total occurrences, second sequence is the literal appearing in the source with dot denoting the same digit as in the number matched against):
92 ........ 2.30258509299404568402 ln(10) or 1/log(e) 5 ...............5 2.30258509299404568402 ln(10) or 1/log(e) 1 .....80528052805 2.30258509299404568402 ln(10) or 1/log(e) 3 .....6 2.30258509299404568402 ln(10) or 1/log(e) 2 .....67 2.30258509299404568402 ln(10) or 1/log(e) 1 .....38 2.30258509299404568402 ln(10) or 1/log(e) 2 .....8 2.30258509299404568402 ln(10) or 1/log(e) 1 .....42 2.30258509299404568402 ln(10) or 1/log(e) 2 ......7 2.30258509299404568402 ln(10) or 1/log(e) 2 ......2 2.30258509299404568402 ln(10) or 1/log(e) 1 ....... 2.30258509299404568402 ln(10) or 1/log(e) 2 .....6553 2.30258509299404568402 ln(10) or 1/log(e) 1 .......4566 2.30258509299404568402 ln(10) or 1/log(e)
Most of those 92 seven digit matches occur in a subdirectory called data implying that they do not occur within code expressions, while .....80528052805 contains enough extra trailing non-matching digits to suggest a different value really was intended. Are there enough unmatched trailing digits in .....6553 to consider it a different value? More experience needs to be gained before attempting to make this call automatically.
At the moment a person has to look at the code containing these ‘close’ values to decide whether the author made a mistake or really did mean to use the value given (unfortunately numbers does not yet have a fancy gui to simplify this task). Sometimes the literals appear in data and other times in an expression that requires domain knowledge to figure out whether it is correct or not. My cursory sampling of the very large data set did not find any serious problems.
Some of the unmatched literals contain so few significant digits they would match many entries in a database of ‘interesting’ values. For instance the numbers database used to contain 745.0, the mean radius of the minor planet Sedna (according to the latest NASA data), but it was removed because of the large number of false positive matches it generated.
Many of the unmatched literals appear to do not appear to have any special interest outside of code that contains them, for instance 0.2.
I am hoping that readers of this blog will download numbers and run their code through it. They might find some faults in their code and add new values to their local ‘interesting’ numbers database to target their own application domain(not forgetting to email me a copy to include in the next release). Suggestions for improving the detection of inaccurate literals always welcome (check to the TODO file first).
An interesting observation from comparing the mathematical equations in the book Computation of Special Functions with the Fortran source provided by its authors is that when a ‘known’ constant (e.g., pi, pi/2) appears in isolation (e.g., as an argument or a value in an assignment) its literal representation often contains as many digits as supported in 64-bits, while when the same constant appears within an expression evaluating a polynomial it often contains the same number of digits as the other literals appearing in that expression (which is usually less than supported in 64-bits).
Unused function parameters
I have started redoing the source code measurements that appear in my C book, this time using a lot more source, upgraded versions of existing tools, plus some new tools such as Coccinelle and R. The intent is to make the code and data available in a form that is easy for others to use (I am hoping that one or more people will measure the same constructs in other languages) and to make some attempt at teasing out relationships in the data (previously the data was simply plotted with little or no explanation).
While it might be possible to write a paper on every language construct measured, I don’t have the time to do the work. Instead, I will use this blog to make a note of the interesting things that crop up during the analysis of each construct I measure.
First up are unused function parameters (code and data), which at around 11% of all parameters are slightly more common than unused local variables (Figure 190.1). In the following plot black circles are the total number of functions having a given number of parameters, red circles a given number of unused parameters, blue line a linear regression fit of the red circles, and the green line is derived from black circle values using a formula I concocted to fit the data and have no theoretical justification for it.
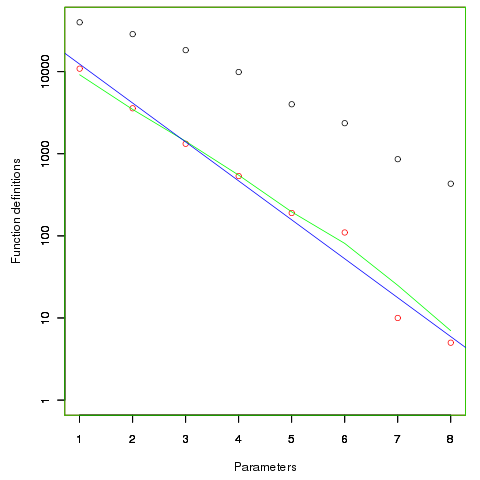
The number of functions containing a given number of unused parameters drops by around a factor of three for each additional unused parameter. Why is this? The formula I came up with for estimating the number of functions containing 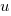 unused parameters is:
unused parameters is: 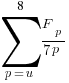 , where
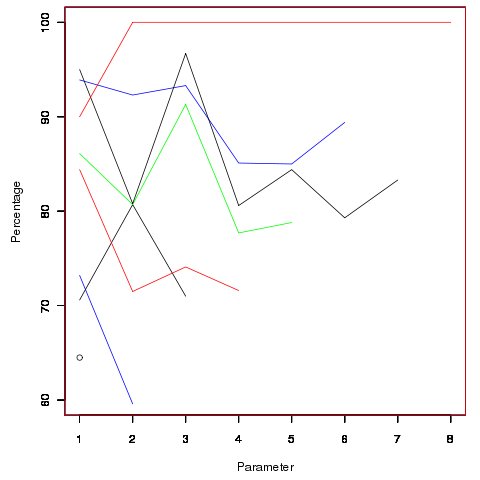
, where 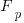 is the total number of function definitions containing
is the total number of function definitions containing 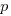 parameters.
parameters.
Which parameter, for those functions defined with more than one, is most likely to be unused? My thinking was that the first parameter might either hold the most basic information (and so rarely be unused) or hold information likely to be superseded when new parameters are added (and so commonly be unused), either way I considered later parameters as often being put there for later use (and therefore more likely to be unused). The following plot is for eight programs plus the sum of them all; for all functions defined with between one and eight parameters, the percentage of times the  ‘th parameter is unused is given. The source measured contained 104,493 function definitions containing more than one parameter with 16,643 of these functions having one or more unused parameter, there were a total of 235,512 parameters with 25,886 parameters being unused.
‘th parameter is unused is given. The source measured contained 104,493 function definitions containing more than one parameter with 16,643 of these functions having one or more unused parameter, there were a total of 235,512 parameters with 25,886 parameters being unused.
There is no obvious pattern to which parameters are likely to be unused, although a lot of the time the last parameter is more likely to be unused than the penultimate one.
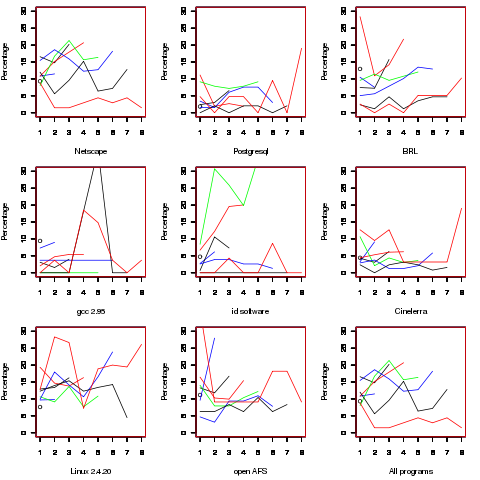
Looking through the raw data I noticed that there seemed to be some clustering of names of unused parameters, in particular if the  ‘th parameter was unused in two adjacent ‘unused parameter’ functions they often had the same name. The following plot is for all measured source and gives the percentage of same name occurrences; the matching process analyses function definitions in the order they occur within a source file and having found one unused parameter its name is compared against the corresponding parameter in the next function definition with the same number of parameters and having an unused parameter at the same position.
‘th parameter was unused in two adjacent ‘unused parameter’ functions they often had the same name. The following plot is for all measured source and gives the percentage of same name occurrences; the matching process analyses function definitions in the order they occur within a source file and having found one unused parameter its name is compared against the corresponding parameter in the next function definition with the same number of parameters and having an unused parameter at the same position.
Before getting too excited about this pattern, we should ask if something similar exists for the used parameters. When I get around to redoing the general parameter measurements, I will look into this question. The numbers of occurrences for functions containing eight parameters is close to minimal.
The functions containing these same-name unused parameters appear to also have related function names. Is this a case of related function being grouped together, often sharing parameter names, and when one of them has an unused parameter the corresponding parameter in the others is also unused?
Is there a correlation between number of parameters and number of statements, are functions containing lots of statements less likely to have unused parameters? What effect does software evolution have (most of this kind of research measures executable code, not variable definitions)?
Quality comparison of floating-point maths libraries
What is the best way to compare the quality of floating-point math libraries (e.g., sin, cos and log)? The traditional approach for evaluating the quality of an algorithm implementing a mathematical function is based on mathematics; methods have been developed to calculate the maximum error between the calculated and the actual value. The answer produced by this approach does not say anything about how frequently this maximum error will occur, only that it occurs at least once.
The log (natural logarithm) is probably the most frequently used mathematical function and I decided to compare a few implementations; R statistical package version 2.11.1 and glibc (libm version 2.11.2) both running under Suse 11.3 on an AMD Athlon 64 X2, and Cygwin version 1.7.1 under Windows XP SP 2 on another AMD Athlon 64 X2.
The algorithm often used to implement mathematical functions involves evaluating a polynomial expression (e.g., Chebyshev polynomials) within a small range of values (various methods are used to map the argument into this range and then scale the calculated result). I decided to initially treat the implementations under test as black boxes and did not know the ranges they used; a range of 0.1 to 1.0 seemed like a good idea and I generated all single precision floating-point values between these two bounds (all 28,521,267 of them, with each adjacent pair still having 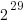 double precision values between them).
double precision values between them).
#include <math.h> #include <stdio.h> int main(int argc, char *argv[]) { float val = 0.1, max_val = 1.0; while (val < max_val) { printf("%12.10f\n", val); val=nextafterf(val, 1.1); } } |
This list of 28 million values was fed as input to three programs:
- bc, which was used to generate the list of assumed to be correct logarithm of these 28 million values. R supports 64-bit IEEE compliant floating-point values, as do the C compilers/libraries used, and the number of decimal digits supported in this representation is 15. To provide greater accuracy to compare against the values generated by bc contained 17 digits, an extra two decimal digits over the IEEE values.
scale=17 while ((val=read() > 0)) l(val)
- A C program.
#include <math.h> #include <stdio.h> int main(int argc, char *argv[]) { double val; while (!feof(stdin)) { scanf("%lf", &val); printf("%17.15f\n", log(val)); } }
- A R program.
base_range=file("stdin", open="r") base_val=as.numeric(readLines(base_range, n=1)) while (length(base_val) != 0) { cat(format(log(base_val), nsmall=15), file=stdout()) cat("\n", file=stdout()) base_val=as.numeric(readLines(base_range, n=1)) }
The output of the C and R programs was then compared against the output from bc; which unfortunately creates a dependency on the accuracy of the C & R binary to decimal output routines (the subsequent comparison process gets around the decimal-to-binary input problem by reading the log values as strings and comparing the last few digits of each respective value). Accurate floating-point I/O needs something like hexadecimal floating constants.
Plotting the number of computed values of log that differ by a given amount from the value computed by bc, we get (values whose error is below -50 will be rounded down and those above 50 rounded up, ignoring the issue of round to even):
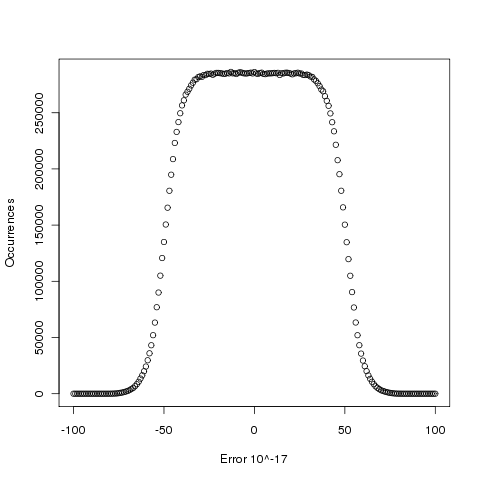
The results (raw data for R, Linux C and Cygwin C) show that around 5.6% of values are off by one in the last (15th) digit (Cygwin was slightly worse at 5.7%). The results for R/Linux C were almost identical and a quick check of the R source tree showed that R calls the C library function to evaluate log (it is a bit worrying that R is dependent on the host maths library, they should think about replacing this dependency by something like MPFR tout suite; even though the 64-bit glibc library is of very high quality it still has an environmental dependency).
Being off by one in the last decimal place is unlikely to keep many people awake at night. But if we want a measure of quality, is percentage of inaccurate values a useful measure of math library quality? Provided it is coupled with the amount of inaccuracy, I think this is a useful measure.
Empirical software engineering is five years old
Science and engineering are built on theoretical models that are tested against measurements of ‘reality’. Until around 10 years ago there was very little software engineering ‘reality’ publicly available; companies rarely made source available and were generally unforthcoming about any bugs that had been discovered. What happened around 10 years ago was the creation of public software repositories such as SourceForge and public fault databases such as Bugzilla. At last researchers had access to what could be claimed to be real world data.
Over the last five years there has been an explosion of papers using SourceForge/Bugzilla kinds of data looking for a connection between everything+kitchen sink and faults. The traditional measures such as Halstead and McCabe have not stood up well against this onslaught of data, hardly surprising given they were more or less conjured out of thin air. Some researchers are trying to extract information about developer characteristics from mailing lists; given that software is written by developers there is obviously a real need for the characteristics of major project contributors to play a significant role in any theory of software faults.
Software engineering data includes a lot more than what can be extracted from source code, bug lists and email lists. A growing number of repositories have been set up to hold measurement and experimental data, e.g., hardware failures, effort prediction (while some of this data is pre-2000 it tends to be low volume or poor quality), and file system related.
At the individual level a small number of researchers have made data available on their own web site, a few more will send a copy if asked and sadly there are many cases where the raw data has been lost. In two recent cases researchers have responded to my request for raw data by telling me they are working on additional papers and don’t want to make the data public yet. I can understand that obtaining interesting data requires a lot of work and researchers want to extract maximum benefit; I look forward to see the new papers and the eventual availability of the data.
My interest in all this data is that I have started work on a book covering empirical software engineering using R. Five years ago such book would have contained lots of equations, plenty of hand waving and if data sets were available they would probably have been small enough to print on one page. Today there are still plenty of equations (mostly relating to statistical this that and the other), no hand waving (well, none planned), data sets for everything covered (some in the gigabytes and a few that can still fit on a page) and pretty pictures (color graphs, as least for the pdf version).
When historians trace back the history of empirical software engineering I think they will say that it started for real sometime around 2005. Before then, any theories that were based on observation tended to have small, single study, data sets with little statistical significance or power.
Has the seed that gets software development out of the stone-age been sown?
A big puzzle for archaeologists is why Stone Age culture lasted as long as it did (from approximately 2.5 millions years ago until the start of the copper age around 6.3 thousand years ago). Given the range of innovation rates seen in various cultures through-out human history, a much shorter Stone Age is to be expected. A recent paper proposes that low population density is what maintained the Stone Age status quo; there was not enough contact between different hunter gather groups for widespread take up of innovations. Life was tough, and the viable lifetime of individual groups of people may not have been long enough for them to be likely to pass on innovations (either their own ones encountered through contact with other groups).
Software development is often done by small groups that don’t communicate with other groups and regularly die out (well there is a high turn-over, with many of the more experienced people moving on to non-software roles). There are sufficient parallels between hunter gathers and software developers to suggest both were/are kept in a Stone Age for the same reason, lack of a method that enables people to obtain information about innovations and how worthwhile these might be within a given environment.
A huge barrier to the development of better software development practices is the almost complete lack of significant quantities of reliable empirical data that can be used to judge whether a claimed innovation is really worthwhile. Companies rarely make their detailed fault databases and product development history public; who wants to risk negative publicity and lawsuits just so academics have some data to work with.
At the start of this decade, public source code repositories like SourceForge and public software fault repositories like Bugzilla started to spring up. These repositories contain a huge amount of information about the characteristics of the software development process. Questions that can be asked of this data include: what are common patterns of development and which ones result in fewer faults, how does software evolve and how well do the techniques used to manage it work.
Empirical software engineering researchers are now setting up repositories, like Promise, containing the raw data from their analysis of Open Source (and some closed source) projects. By making this raw data available, they are reducing the effort needed by other researchers to investigate their own alternative ideas (I have just started a book on empirical software engineering using the R statistical language that uses examples based on this raw data).
One of the side effects of Open Source development could be the creation of software development practices that have been shown to be better (including showing that some existing practices make things worse). The source of these practices not being what the software developers themselves do or how they do it, but the footsteps they have left behind in the sand.
Thinking in R: vectors
While I have been using the R language/environment for over five years or so, whenever I needed to do some statistical calculations, until recently I was only a casual user. A few months ago I started to use R in more depth and made a conscious decision to try and do things the ‘R way’.
While it is claimed that R is a functional language with object oriented features these are sufficiently well hidden that the casual user would be forgiven for thinking R was your usual kind of domain specific imperative language cooked up by a bunch of people who had not done this sort of thing before.
The feature I most wanted to start using in an R-like way was vectors. A literal value in R is not a scalar, it is a vector of length 1 and the built-in operators take vector operands and return a vector result, e.g., the result of the multiplication (c is the concatenation operator and in the following case returns a vector of containing two elements)
> c(1, 2) * c(3, 4) [1] 3 8 > |
The language does contain a for-loop and an if-statement, however the R-way is to use the various built-in functions operating on vectors rather than explicit loops.
A problem that has got me scratching my head for a better solution than the one I have is the following. I have a vector of numbers (e.g., 1 7 1 2 9 3 2) and I want to find out how many of each value are contained in the vector (i.e., 1 2, 2 2, 3 1, 7 1, 9 1).
The unique function returns a vector containing one instance of each value contained in the argument passed to it, so that removes duplicates. Now how do I get a count of each of these values?
When two vectors of unequal length are compared the shorter operand is extended (or rather the temporary holding its value is extended) to contain the same number of elements as the longer operand by ‘reusing’ values from the shorter operand (i.e., when indexing reaches the end of a vector the index is reset to the beginning and then moves forward again). This means that in the equality test X == 2 the right operand is extended to be a vector having the number of elements as X, all with the value 2. Some of these comparisons will be true and others false, but importantly the resulting vector can be used to index X, i.e., X[X == 2] returns a vector of 2’s, one for each occurrence of 2 in X. We can use length to obtain the number of elements in a vector.
The following function returns the number of instances of n in the vector X (now you will see why thinking the ‘R way’ needs practice):
num_occurrences = function(n)
{
length(X[X == n]) # X is a global variable
} |
My best solution to the counting problem, so far, uses the function lapply, which applies its second argument to every element of its first argument, as follows:
unique_X = unique(X) # I know, real staticians use <- for assignment X_counts = lapply(unique_X, num_occurrences) |
Using lapply feels like a bit of a cheat to me. Ok, the loop is in compiled C code rather than interpreted R code, but an R function is being called for every unique value.
I have been rereading Matter Computational which has gotten me looking for a solution like those in the first few chapters of this book (and which will probably be equally obscure).
Any R experts out there with suggestions for a non-lapply solution?
Variations in the literal representation of Pi
The numbers system I am developing attempts to match numeric literals contained in a file against a database of interesting numbers. One of the things I did to quickly build a reasonably sized database of reliable values was to extract numeric literals from a few well known programs that I thought I could trust.
R is a widely used statistical package, and Maxima is a computer algebra system with a long history. Both contain a great deal of functionality and are actively maintained.
To my surprise, the source code of both packages contain a large variety of different literal values for  , or to be exact, the number of digits contained in the literals varied by more than I expected. In the following table, the value to the left of the
, or to be exact, the number of digits contained in the literals varied by more than I expected. In the following table, the value to the left of the  representation is the number of occurrences; values listed in increasing literal order:
representation is the number of occurrences; values listed in increasing literal order:
Maxima R
2 3.14159
14 3.141592
1 3.1415926
1 3.14159265 2 3.14159265
3 3.1415926535
4 3.14159265358979
14 3.141592653589793
3 3.1415926535897932385 3 3.1415926535897932385
9 3.14159265358979324
1 3.14159265359
1 3.1415927
1 3.141593
The comments in the Maxima source led me to believe that some thought had gone into ensuring that the numerical routines were robust. Over 3/4 of the literal representations of  have a precision comparable to at least that of 64-bit floating-point (I’m assuming an IEEE 754 representation in this post).
have a precision comparable to at least that of 64-bit floating-point (I’m assuming an IEEE 754 representation in this post).
In the R source, approximately 2/3 of the literal representations of  have a precision comparable to that of 32-bit floating-point.
have a precision comparable to that of 32-bit floating-point.
Closer examination of the source suggests one reason for this difference. Both packages make heavy use of existing code (translated from Fortran to Lisp for Maxima and from Fortran to C for R); using existing code makes good sense and because of its use in scientific and engineering applications many numerical libraries have been written in Fortran. Maxima has adapted the slatec library, whereas the R developers have used a variety of different libraries (e.g., specfun).
How important is variation in the representation of Pi?
- A calculation based on a literal that is only accurate to 32-bits is likely to be limited to that level of accuracy (unless errors cancel out somewhere).
- Inconsistencies in the value used to represent Pi are a source of error. These inconsistencies may be implicit, for instance literals used to denote a value derived from
 such as
such as 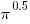 often seem to be based on more precise values of Pi than appear in the code.
often seem to be based on more precise values of Pi than appear in the code.
The obvious solution to this representation issue of creating a file containing definitions of all the frequently used literal values has possible drawbacks. For instance, numerical accuracy is a strange beast, and increasing the precision of one literal without doing the same for other literals appearing in a calculation can sometimes reduce the accuracy of the final result.
Pulling together existing libraries to build a package is often very cost-effective, but numerical accuracy is a slippery beast, and this inconsistent usage of literals suggests that developers from these two communities have not addressed the system level consequences of software reuse.
Update 6 April: After further rummaging around in the R source distribution, I found that things are not as bad as they first appear. Only two of the single precision instances of  listed above occur in the C or Fortran source code, the rest appear in support files (e.g., m4 scripts and R examples).
listed above occur in the C or Fortran source code, the rest appear in support files (e.g., m4 scripts and R examples).
Recent Comments