Archive
Compiler benchmarking for the 21st century
I would like to propose a new way of measuring the quality of a compiler’s code generator: The highest quality compiler is one that generates identical code for all programs that produce the same output, e.g., a compiler might spot programs that calculate pi and always generate code that uses the most rapidly converging method known. This is a very different approach to the traditional methods based on using (mostly) execution time or size (usually code but sometimes data) as a measure of quality.
Why is a new measurement method needed, and why choose this one? It is relatively easy for compiler vendors to tune their products to the commonly used benchmark and they seem to have lost their role as drivers for new optimization techniques. Different developers have different writing habits and companies should not have to waste time and money changing developer habits just to get the best quality code out of a compiler; compilers should handle differences in developer coding habits and not let it affect the quality of generated code. There are major savings to be had by optimizing the effect that developers are trying to achieve rather than what they have actually written (these days new optimizations targeting at what developers have written show very low percentage improvements).
Deducing that a function calculates pi requires a level of sophistication in whole program analysis that is unlikely to be available in production compilers for some years to come (ok, detecting 4*atan(1.0) is possible today). What is needed is a collection of compilable files containing source code that aims to achieve an outcome in lots of different ways. To get the ball rolling the “3n times 2” problem is presented as the first of this new breed of benchmarks.
The “3n times 2” problem is a variant on the 3n+1 problem that has been tweaked to create more optimization opportunities. One implementation of the “3n times 2” problem is:
if (is_odd(n)) n = 3*n+1; else n = 2*n; // this is n = n / 2; in the 3n+1 problem |
There are lots of ways of writing code that has the same effect, some of the statements I have seen for calculating n=3*n+1 include: n = n + n + n + 1, n = (n << 1) + n + 1 and n *= 3; n++, while some of the ways of checking if n is odd include: n & 1, (n / 2)*2 != n and n % 2.
I have created a list of different ways in which 3*n+1 might be calculated and is_odd(n) might be tested and written a script to generate a function containing all possible permutations (to reduce the number of combinations no variants were created for the least interesting case of n=2*n, which was always generated in this form). The following is a snippet of the generated code (download everything):
if (n & 1) n=(n << 2) - n +1; else n*=2; if (n & 1) n=3*n+1; else n*=2; if (n & 1) n += 2*n +1; else n*=2; if ((n / 2)*2 != n) { t=(n << 1); n=t+n+1; } else n*=2; if ((n / 2)*2 != n) { n*=3; n++; } else n*=2; |
Benchmarks need a means of summarizing the results and here I make a stab at doing that for gcc 4.6.1 and llvm 2.9, when executed using the -O3 option (output here and here). Both compilers generated a total of four different sequences for the 27 'different' statements (I'm not sure what to do about the inline function tests and have ignored them here) with none of the sequences being shared between compilers. The following lists the number of occurrences of each sequence, e.g., gcc generated one sequence 16 times, another 8 times and so on:
gcc 16 8 2 1 llvm 12 6 6 3
How might we turn these counts into a single number that enables compiler performance to be compared? One possibility is to award 1 point for each of the most common sequence, 1/2 point for each of the second most common, 1/4 for the third and so on. Using this scheme, gcc gets 20.625, and llvm gets 16.875. So gcc has greater consistency (I am loathed to use the much overused phrase higher quality).
Now for a closer look at the code generated.
Both compilers always generated code to test the least significant bit for the conditional expressions n & 1 and n % 2. For the test (n / 2)*2 != n gcc generated the not very clever right-shift/left-shift/compare while llvm and'ed out the bottom bit and then compared; so both compilers failed to handle what is a surprisingly common check for a number being odd.
The optimal code for n=3*n+1 on a modern x86 processor is (lots of register combinations are possible, let's assume rdx contains n) leal 1(%rdx,%rdx,2), %edx and this is what both compilers generated a lot of the time. This locally optimal code is not always generated because:
- gcc fails to detect that
(n << 2)-n+1is equivalent to(n << 1)+n+1and generates the sequenceleal 0(,%rax,4), %edx ; subl %eax, %edx ; addl $1, %edx(I pointed this out to a gcc maintainer sometime ago, and he suggested reporting it as a bug). This 'bug' occurs three times in total. - For some forms of the calculation llvm generates globally better code by taking the else arm into consideration. For instance, when the calculation is written as
n += (n << 1) +1llvm deduces that(n << 1)and the2*nin theelseare equivalent, evaluates this value into a register before performing the conditional test thus removing the need for an unconditional jump around the 'else' code:leal (%rax,%rax), %ecx testb $1, %al je .LBB0_8 # BB#7: orl $1, %ecx # deduced ecx is even, arithmetic unit not needed! addl %eax, %ecx .LBB0_8:
This more efficient sequence occurs nine times in total.
The most optimal sequence was generated by gcc:
testb $1, %dl leal (%rdx,%rdx), %eax je .L6 leal 1(%rdx,%rdx,2), %eax .L6: |
with llvm and pre 4.6 versions of gcc generating the more traditional form (above, gcc 4.6.1 assumes that the 'then' arm is the most likely to be executed and trades off a leal against a very slow jmp):
testb $1, %al je .LBB0_5 # BB#4: leal 1(%rax,%rax,2), %eax jmp .LBB0_6 .LBB0_5: addl %eax, %eax .LBB0_6: |
There is still room for improvement, perhaps by using the conditional move instruction (which gcc actually generates within the not-very-clever code sequence for (n / 2)*2 != n) or by using the fact that eax already holds 2*n (the potential saving would come through a reduction in complexity of the internal resources needed to execute the instruction).
llvm insists on storing the calculated value back into n at the end of every statement. I'm not sure if this is a bug or a feature designed to make runtime debugging easier (if so it ought to be switched off by default).
Missed optimization opportunities (not intended to be part of this benchmark and if encountered would require a restructuring of the test source) include noticing that if  is odd then
is odd then 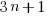 is always even, creating the opportunity to perform the following multiply by 2 without an if test.
is always even, creating the opportunity to perform the following multiply by 2 without an if test.
Perhaps one day, compilers will figure out when a program is calculating pi and generate code that uses the best known algorithm. In the meantime, I am interested in hearing suggestions for additional different-algorithm-same-code benchmarks.
Variations in the literal representation of Pi
The numbers system I am developing attempts to match numeric literals contained in a file against a database of interesting numbers. One of the things I did to quickly build a reasonably sized database of reliable values was to extract numeric literals from a few well known programs that I thought I could trust.
R is a widely used statistical package, and Maxima is a computer algebra system with a long history. Both contain a great deal of functionality and are actively maintained.
To my surprise, the source code of both packages contain a large variety of different literal values for  , or to be exact, the number of digits contained in the literals varied by more than I expected. In the following table, the value to the left of the
, or to be exact, the number of digits contained in the literals varied by more than I expected. In the following table, the value to the left of the  representation is the number of occurrences; values listed in increasing literal order:
representation is the number of occurrences; values listed in increasing literal order:
Maxima R
2 3.14159
14 3.141592
1 3.1415926
1 3.14159265 2 3.14159265
3 3.1415926535
4 3.14159265358979
14 3.141592653589793
3 3.1415926535897932385 3 3.1415926535897932385
9 3.14159265358979324
1 3.14159265359
1 3.1415927
1 3.141593
The comments in the Maxima source led me to believe that some thought had gone into ensuring that the numerical routines were robust. Over 3/4 of the literal representations of  have a precision comparable to at least that of 64-bit floating-point (I’m assuming an IEEE 754 representation in this post).
have a precision comparable to at least that of 64-bit floating-point (I’m assuming an IEEE 754 representation in this post).
In the R source, approximately 2/3 of the literal representations of  have a precision comparable to that of 32-bit floating-point.
have a precision comparable to that of 32-bit floating-point.
Closer examination of the source suggests one reason for this difference. Both packages make heavy use of existing code (translated from Fortran to Lisp for Maxima and from Fortran to C for R); using existing code makes good sense and because of its use in scientific and engineering applications many numerical libraries have been written in Fortran. Maxima has adapted the slatec library, whereas the R developers have used a variety of different libraries (e.g., specfun).
How important is variation in the representation of Pi?
- A calculation based on a literal that is only accurate to 32-bits is likely to be limited to that level of accuracy (unless errors cancel out somewhere).
- Inconsistencies in the value used to represent Pi are a source of error. These inconsistencies may be implicit, for instance literals used to denote a value derived from
 such as
such as 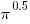 often seem to be based on more precise values of Pi than appear in the code.
often seem to be based on more precise values of Pi than appear in the code.
The obvious solution to this representation issue of creating a file containing definitions of all the frequently used literal values has possible drawbacks. For instance, numerical accuracy is a strange beast, and increasing the precision of one literal without doing the same for other literals appearing in a calculation can sometimes reduce the accuracy of the final result.
Pulling together existing libraries to build a package is often very cost-effective, but numerical accuracy is a slippery beast, and this inconsistent usage of literals suggests that developers from these two communities have not addressed the system level consequences of software reuse.
Update 6 April: After further rummaging around in the R source distribution, I found that things are not as bad as they first appear. Only two of the single precision instances of  listed above occur in the C or Fortran source code, the rest appear in support files (e.g., m4 scripts and R examples).
listed above occur in the C or Fortran source code, the rest appear in support files (e.g., m4 scripts and R examples).
Recent Comments