Archive
Analysis of a subset of the Linux Counter data
The Linux Counter project was started in 1993, with the aim of tracking the growth of Linux users (the kernel was first released two years earlier). Anybody could register any of their machines running Linux; a user ran a script that gathered basic information about a machine, and the output was emailed to the project. Once registered, users received an annual reminder to update information in their entry (despite using Linux since before the 1.0 release, user #46406 didn’t register until 2001).
When it closed (reopened/closed/coming back) it had 120K+ registered users. That’s a lot of information about computers, which unfortunately is not publicly available. I have not had any replies to my emails to those involved, asking for a copy that could be released in anonymized form.
This week I found 15,906 rows of what looks like a subset of the Linux counter data, most entries are post-2005. What did I learn from this data?
An obvious use is the pattern to check is changes over time. While the data does not include any explicit date, it does include the Kernel version, from which the earliest date can be inferred.
An earlier post used SPEC data to estimate the growth in installed memory over time; it has been doubling every 840 days, give or take. That data contains one data point per distinct vendor computer; the Linux counter data contains one entry per computer in use. There is around thirty pairs of entries for updated systems, i.e., a user updated the entry for an existing system.
The plot below shows memory installed in each registered computer, over time, for servers, laptops and workstations, with fitted regression lines. The memory size doubling times are: servers 4,000 days, laptops 2,000 days, and workstations 1,300 days (code+data):
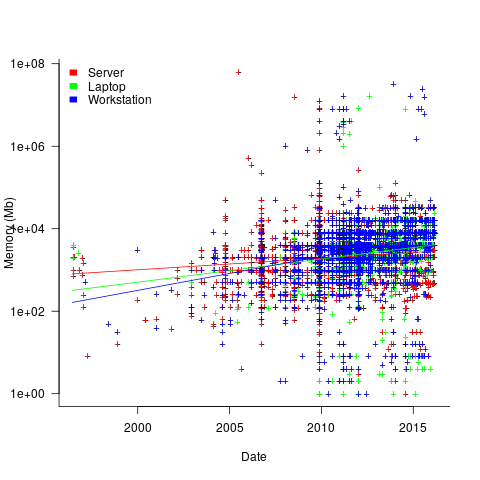
A regression model using dates is a good fit in the statistical sense, but explain very little of the variance in the data. The actual date on which the memory size was selected may have been earlier (because the kernel has been updated to a later release), or later (because memory was added, but the kernel was not updated).
Why is the memory doubling time so long?
Has memory size now reached the big-enough boundary, do Linux counter users keep the same system for many years without upgrading, are Linux counter systems retired Windows boxes that have been repurposed (data on installed memory Windows boxes would answer this point)?
Suggestions welcome.
When memory capacity is limited, it may be useful to swap least recently used memory contents to disc; Linux setup includes the specification of a swap partition. What is the optimal size of the size partition? A common recommendation is: if memory is less than 2G swap size is twice memory; if between 2-8G swap size is the same as memory, and for greater than 8G, half of memory size. The table below shows the percentage of particular system classes having a given swap/memory ratio (rounding the list of ratios to contain one decimal digit produces a list of over 100 ratio values).
swap/memory Server Workstation Laptop 1.0 15.2 19.9 25.9 2.0 10.3 9.6 8.6 0.5 9.5 7.7 8.4 |
The plot below shows memory against swap partition size, for the system classes laptop, server and workstation, with fitted regression line (code+data):
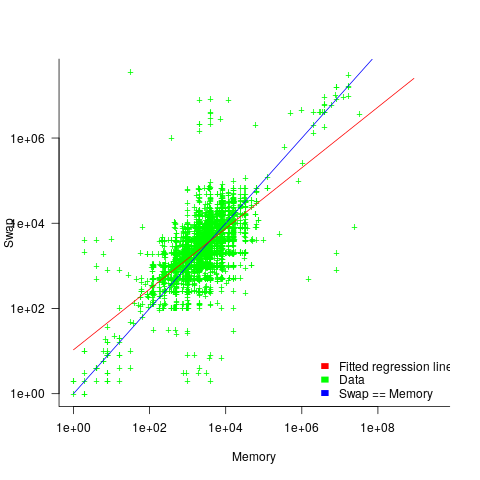
The available disk space also has a (small) impact on swap partition size; the following model explains 46% of the variance in the data: 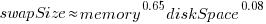 .
.
I was hoping to confirm the rate of installed memory growth suggested by the SPEC data, with installed systems lagging a few years behind the latest releases. This Linux counter data tells a very different growth story. Perhaps pre-2005 data will tell another story (I just need to find it).
I’m not sure if the swap/memory ratio analysis is of any use to systems people. It was something of a fishing expedition on my part.
Other counting projects have included the Ubuntu counter project, and Hardware for Linux which is still active and goes back to August 2014.
I’m interested in hearing about the availability of any other Linux counter data, or data from other computer counting projects.
Least Recently Used: The experiment that made its reputation
Today we all know that least recently used is the best page replacement algorithm for virtual memory systems (actually paging is complicated in today’s intertwined computing world).
Virtual memory was invented in 1959 and researchers spent the 1960s trying to figure out the best page replacement algorithm.
Programs were believed to spend most of their time in loops and this formed the basis for the rationale for why FIFO, First In First Out, was the best page replacement algorithm (widely used at the time).
Least recently used, LRU, was on people’s radar as a possible technique and was mathematically analysed, along with various other techniques. The optimal technique was known and given the name OPT; a beautifully simple technique with one implementation drawback, it required knowledge of future memory usage behavior (needless to say some researchers set to work trying to predict future memory usage, so this algorithm could be used).
An experiment by Tsao, Comeau and Margolin, published in 1972, showed that LRU outperformed FIFO and random replacement. The rest, as they say, is history; in this case almost completely forgotten history.
The paper “A multifactor paging experiment: I. The experiment and the conclusions” was published as one of a collection of papers in “Statistical Computer Performance Evaluation” edited by Freiberger. A second paper by two of the authors in the same book outlines the statistical methodology. Appearing in a book means this paper can be very hard to track down. I recently bought a copy of the book on Amazon for one penny (the postage was £2.80).
The paper contains a copy of the experimental results and below are the page swap numbers:
loadseq group group group freq freq freq alpha alpha alpha Pages 24 20 16 24 20 16 24 20 16 LRU S 32 48 538 52 244 998 59 536 1348 LRU M 53 81 1901 112 776 3621 121 1879 4639 LRU L 142 197 5689 262 2625 10012 980 5698 12880 FIFO S 49 67 789 79 390 1373 85 814 1693 FIFO M 100 134 3152 164 1255 4912 206 3394 5838 FIFO L 233 350 9100 458 3688 13531 1633 10022 17117 RAND S 62 100 1103 111 480 1782 111 839 2190 RAND M 96 245 3807 237 1502 6007 286 3092 7654 RAND L 265 2012 12429 517 4870 18602 1728 8834 23134 |
Three Fortran programs were used, Small (55 statements), Medium (215 statements) and Large (595 statements). These programs were loaded by group (sequences of frequently called subroutines grouped together), freq (subroutines causing the most page swaps were grouped together), alpha (subroutines were grouped alphabetically).
The system was configured with either 24, 20 or 16 pages of 4,096 bytes; it had a total of 256K of memory (a lot of memory back then). The experiment consumed 60 cpu hours.
Looking at the table, it is easy to see that LRU has the best performance. In places random replacement beats FIFO. A regression model (code and data) puts numbers on the performance advantage.
The paper says that the only interaction was between memory size (i.e., number of pages) and how the programs were loaded. I found pairwise interaction between all variables, but then I am using a technique that was being invented as this paper was being published (see code for details).
Number of page swaps was one of three techniques used for measuring performed. The other two were activity count (average number of pages in main memory referenced at least once between page swaps) and inactivity count (average time, measured in page swaps, of a page in secondary storage after it had been swapped out). See data for details.
I vividly remember dropping in on a randomly chosen lecture in computer science in the mid-70s (I studied physics and electronics), the subject was page selection algorithms and there were probably only a dozen people in the room (physics and electronics sometimes had close to 100). The lecturer regaled those present with how surprising it was that LRU was the best and somebody had actually done an experiment showing this. Having a physics/electronics background, the experimental approach to settling questions was second nature to me.
Software memory management
I recently wrote about how computer memory capacity limits were a serious constraint for compiler writers. One technique used to increase the amount of memory available to a compiler (back in the days when pointers usually contained 16-bits) is software based paged memory management. Yes, compiler writers were generally willing to take the runtime performance hit to increase effectively accessible memory by around a factor of 10-25 (e.g., a 2 byte number used as an index into an array of 20 to 50 byte records).
The code to iterate over a data structure stored under the control of a software memory manager looks like the following (taken from a C to Pascal translator):
Var Flds : Sw_Ptr; (* in practice an integer *) T_Node : Sw_Node; (* in practice a pointer to a record *) Begin While Flds <> Sw_Nil Do (* Sw_Nil is the memory managers Nil value *) Begin Sw_Node_Ref(Cpswfile, Flds, T_Node, Mm_Readonly); If T_Node.Pn^.Node_Is<>N_Is_Field Then Verify_Error(Ve_Cputils, Ve_Scan_Fld); Scan(T_Node.Pn^.Field_Node.Ftype); Flds := T_Node.Pn^.Field_Node.Next; End; End; |
Where Sw_Node_Ref is a procedure in the memory management package that ensures the record denoted by Flds (whose value was obtained by a previous called to Sw_New_Node) is available in memory and returned in T_Node. Had Mm_ReadWrite rather than Mm_Readonly been specified the memory manager would assume that the record had been modified and when the page containing the record was swapped out of main memory it would write the contents of the page containing it to the swapfile (specified by the first argument, Cpswfile).
A call to Sw_Node_Ref only guarantees that the record is at the returned location until the next memory management procedure is called. This takes advantage of common usage which is: read a record, do something with its contents and then move on to the next one. The procedure Sw_Node_Ptr is available for when a record needs to be held in main memory across multiple Sw_ calls; this procedure locks a record in the limited capacity memory pool until explicitly freed (a Pascal style Mark/Release system was also available).
Multiple records were overlayed on a page (invariably 512 bytes) of storage. Some implementations used a fancy tool to create the overlay while others did it manually. The size of the pool in main memory used to hold swapped-in pages was specified when the memory manager was initialized; the maximum number of records that could be created by a call to Sw_New_Node was only limited by the maximum value of an integer and available disk space.
I learned about this implementation technique while on secondment at Intermetrics in the early 1980s, and they told me it came from the PQCC project of the mid 1970s. There is a paper in the Proceedings of the 1982 SIGPLAN symposium describing the system/library used by Intermetrics, which rambles on about nothing in particular and fails to say anything about software memory management (it is too useful an idea for a commercial company to tell anybody else); I don’t know of any other published description. Everybody I know who left Intermetrics to work on other compilers created their own implementation of a software memory management package.
Recent Comments