Archive
Searching for inaccurate literals in R
In creating the numbers tool I wanted to be able to do two things, 1) obtain information about what source did by matching the numeric literals it contained against a database of ‘interesting’ values (now with over 14,000 entries) and 2) flag possible incorrect numeric literals (e.g., 3.1459265 when 3.14159265 had been intended in core/Helix.cpp of the MIFit source {now fixed}).
I have recently been enhancing ‘incorrect numeric literal’ support and using the latest release of R as a test bed (whose floating-point literals are almost identical to the last release I looked at, R-2.11.1, log file here).
The first fault I found (0.20403... instead of 0.020403...) looked very serious until I realised it was involved in calculating an initial value feed into an iterative algorithm (at worst causing an extra iteration or so). It looks like the developer overlooked the “e-1” that appears in the original (click on ‘Page 48’).
The second possible problem turned out to be an ambiguity in the file main/color.c which contains the comment “CIE-XYZ to sRGB” above three expressions that perform a conversion from CIE-XYZ to BT.709 RGB. Did the developer get the comment or the numeric literals wrong? People are known to confuse the two forms of RGB (for an explanation see Annex B) .
Apart from a few minor errors such as 0.950301 instead of 0.9503041 (in …/grDevices/R/postscript.R) nothing else of interest turned up so I shifted attention to the add-on packages available on the Comprehensive R Archive Network.
The 3,000+ packages occupy almost 2 Gig in compressed form (fortunately numbers can operate directly on compressed archives and the files did not need to be unpacked) and I decided to limit the analysis to just the R source files, which cut the number of floating-point literals down to around 2 million (after ignoring the contents of comments, 10M compressed log file here).
The various floating-point literals having a value close to 2.30258509299404568402 (the most common match; no idea why the value ln(10) or 1/log(e) should be so popular) highlight the various issues that crop up when using approximate matching to look for faults. The following are some of these matches (first number is total occurrences, second sequence is the literal appearing in the source with dot denoting the same digit as in the number matched against):
92 ........ 2.30258509299404568402 ln(10) or 1/log(e) 5 ...............5 2.30258509299404568402 ln(10) or 1/log(e) 1 .....80528052805 2.30258509299404568402 ln(10) or 1/log(e) 3 .....6 2.30258509299404568402 ln(10) or 1/log(e) 2 .....67 2.30258509299404568402 ln(10) or 1/log(e) 1 .....38 2.30258509299404568402 ln(10) or 1/log(e) 2 .....8 2.30258509299404568402 ln(10) or 1/log(e) 1 .....42 2.30258509299404568402 ln(10) or 1/log(e) 2 ......7 2.30258509299404568402 ln(10) or 1/log(e) 2 ......2 2.30258509299404568402 ln(10) or 1/log(e) 1 ....... 2.30258509299404568402 ln(10) or 1/log(e) 2 .....6553 2.30258509299404568402 ln(10) or 1/log(e) 1 .......4566 2.30258509299404568402 ln(10) or 1/log(e)
Most of those 92 seven digit matches occur in a subdirectory called data implying that they do not occur within code expressions, while .....80528052805 contains enough extra trailing non-matching digits to suggest a different value really was intended. Are there enough unmatched trailing digits in .....6553 to consider it a different value? More experience needs to be gained before attempting to make this call automatically.
At the moment a person has to look at the code containing these ‘close’ values to decide whether the author made a mistake or really did mean to use the value given (unfortunately numbers does not yet have a fancy gui to simplify this task). Sometimes the literals appear in data and other times in an expression that requires domain knowledge to figure out whether it is correct or not. My cursory sampling of the very large data set did not find any serious problems.
Some of the unmatched literals contain so few significant digits they would match many entries in a database of ‘interesting’ values. For instance the numbers database used to contain 745.0, the mean radius of the minor planet Sedna (according to the latest NASA data), but it was removed because of the large number of false positive matches it generated.
Many of the unmatched literals appear to do not appear to have any special interest outside of code that contains them, for instance 0.2.
I am hoping that readers of this blog will download numbers and run their code through it. They might find some faults in their code and add new values to their local ‘interesting’ numbers database to target their own application domain(not forgetting to email me a copy to include in the next release). Suggestions for improving the detection of inaccurate literals always welcome (check to the TODO file first).
An interesting observation from comparing the mathematical equations in the book Computation of Special Functions with the Fortran source provided by its authors is that when a ‘known’ constant (e.g., pi, pi/2) appears in isolation (e.g., as an argument or a value in an assignment) its literal representation often contains as many digits as supported in 64-bits, while when the same constant appears within an expression evaluating a polynomial it often contains the same number of digits as the other literals appearing in that expression (which is usually less than supported in 64-bits).
Benford’s law and numeric literals in source code
Benford’s law applies to values derived from a surprising number of natural and man-made processes. I was very optimistic that it would also apply to numeric literals in source code. Measurements of C source showed that I was wrong (the chi-square fit was 1,680 for decimal integer literals and 132,398 for floating literals).
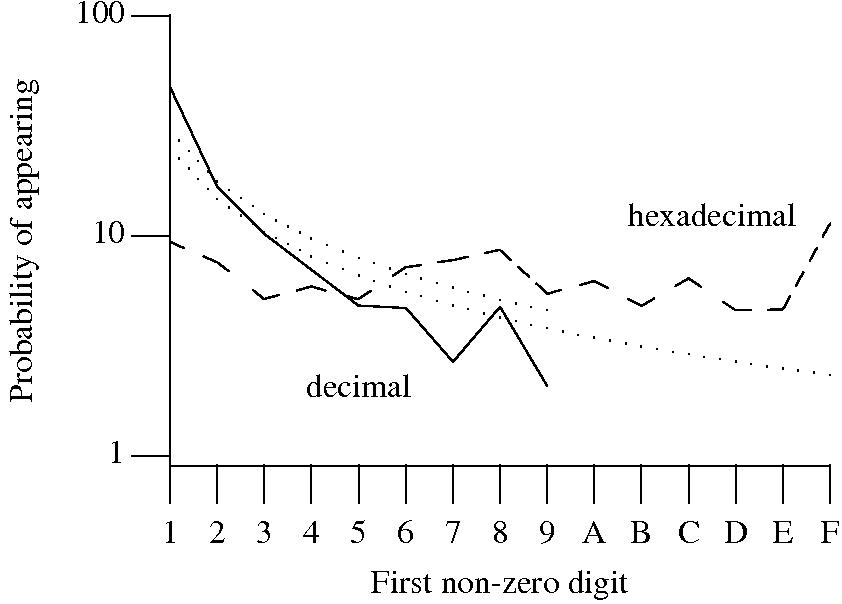
Probability that the leading digit of an (decimal or hexadecimal) integer literal has a particular value (dotted lines predicted by Benford’s law).
What are the conditions necessary for a sample of values to follow Benford’s law? A number of circumstances have been found to result in sample values having a leading digit that follows Benford’s law, including:
Samples that have been found to follow Benford’s law include lists of physical constants and accounting data (so much so that it has been used to detect accounting fraud). However, the number of data-sets containing values whose leading digit follows Benford’s law is not a great as some would make us believe.
Why don’t the leading digits of numeric literals in source code follow Benford’s law?
++/-- operators reduces the number of instances of 1 to increment/decrement a value). But this only applies to integer types, not floating types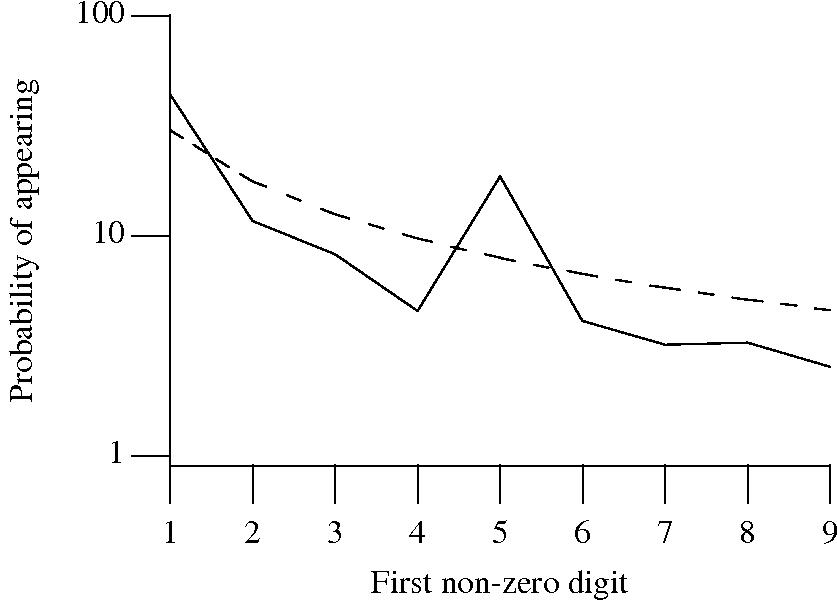
Probability that the leading, first non-zero, digit of a floating literal has a particular value (dashed line predicted by Benford’s law).
5 for the floating-point literals? Have values been rounded to produce 0.5? This looks like an area where methods used for accounting fraud detection might be applied (not that any fraud is implied, just irregularity).These surprising measurements show that there is a lot to the shape of numeric literals that is yet to be discovered.
Recent Comments