Archive
Optimizing floating-point expressions for accuracy
Floating-point arithmetic is one topic that most compiler writers tend to avoid as much as possible. The majority of programs don’t use floating-point (i.e., low customer demand), much of the analysis depends on the range of values being operated on (i.e., information not usually available to the compiler) and a lot of developers don’t understand numerical methods (i.e., keep the compiler out of the blame firing line by generating code that looks like what appears in the source).
There is a scientific and engineering community whose software contains lots of floating-point arithmetic, the so called number-crunchers. While this community is relatively small, many of the problems it works on attract lots of funding and some of this money filters down to compiler development. However, the fancy optimizations that appear in these Fortran compilers (until the second edition of the C standard in 1999 Fortran did a much better job of handling the minutia of floating-point arithmetic) are mostly about figuring out how to distribute the execution of loops over multiple functional units (i.e., concurrent execution).
The elephant in the floating-point evaluation room is result accuracy. Compiler writers know they have to be careful not to throw away accuracy (e.g., optimizing out what appear to be redundant operations in the Kahan summation algorithm), but until recently nobody had any idea how to go about improving the accuracy of what had been written. In retrospect one accuracy improvement algorithm is obvious, try lots of possible combinations of the ways in which an expression can be written and pick the most accurate.
There are lots of ways in which the operands in an expression can be paired together to be operated on; some of the ways of pairing the operands in a+b+c+d include (a+b)+(c+d), a+(b+(c+d)) and (d+a)+(b+c) (unless the source explicitly includes parenthesis compilers for C, C++, Fortran and many other languages (not Java which is strictly left to right) are permitted to choose the pairing and order of evaluation). For n operands (assuming the operators have the same precedence and are commutative) the number is combinations is 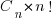 where
where 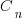 is the n’th Catalan number. For 5 operands there are 1680 combinations of which 120 are unique and for 10 operands
is the n’th Catalan number. For 5 operands there are 1680 combinations of which 120 are unique and for 10 operands 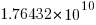 of which
of which 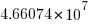 are unique.
are unique.
A recent study by Langlois, Martel and Thévenoux analysed the accuracy achieved by all unique permutations of ten operands on four different data sets. People within the same umbrella project are now working on integrating this kind of analysis into a compiler. This work is another example of the growing trend in compiler research of using the processing power provided by multiple cores to use algorithms that were previously unrealistic.
Over the last six years or so there has been lot of very interesting floating-point work going on in France, with gcc and llvm making use of the MPFR library (multiple-precision floating-point) for quite a while. Something very new and interesting is RangeLab which, given the lower/upper bounds of each input variable to a program (a simple C-like language) computes the range of the outputs as well as ranges for the roundoff errors (the tool assumes IEEE floating-point arithmetic). I now know that over the range [800, 1000] the expression x*(x+1) is a lot more accurate than x*x+x.
Update: See comment from @Eric and my response below.
Automatically improving code
Compared to 20 or 30 years ago we know a lot more about the properties of algorithms and better ways of doing things often exist (e.g., more accurate, faster, more reliable, etc). The problem with this knowledge is that it takes the form of lots and lots of small specific details, not the kind of thing that developers are likely to be interested in, or good at, remembering. Rather than involve developers in the decision-making process, perhaps the compiler could figure out when to substitute something better for what had actually been written.
While developers are likely to be very happy to see what they have written behaving as accurately and reliably as they had expected (ignorance is bliss), there is always the possibility that the ‘less better’ behavior of what they had actually written had really been intended. The following examples illustrate two relatively low level ‘improvement’ transformations:
- this case is probably a long-standing fault in many binary search and merge sort functions; the relevant block of developer written code goes something like the following:
while (low <= high) { int mid = (low + high) / 2; int midVal = data[mid]; if (midVal < key) low = mid + 1 else if (midVal > key) high = mid - 1; else return mid; }
The fault is in the expression
(low + high) / 2which overflows to a negative value, and returns a negative value, if the number of items being sorted is large enough. Alternatives that don’t overflow, and that a compiler might transform the code to, include:low + ((high - low) / 2)and(low + high) >>> 1. - the second involves summing a sequence of floating-point numbers. The typical implementation is a simple loop such as the following:
sum=0.0; for i=1 to array_len sum += array_of_double[i];
which for large arrays can result in
sumlosing a great deal of accuracy. The Kahan summation algorithm tries to take account of accuracy lost in one iteration of the loop by compensating on the next iteration. If floating-point numbers were represented to infinite precision the following loop could be simplified to the one above:sum=0.0; c=0.0; for i = 1 to array_len { y = array_of_double[i] - c; // try to adjust for previous lost accuracy t = sum + y; c = (t - sum) - y; // try and gets some information on lost accuracy sum = t; }
In this case the additional accuracy is bought at the price of a decrease in performance.
Compiler maintainers are just like other workers in that they want to carry on working at what they are doing. This means they need to keep finding ways of improving their product, or at least improving it from the point of view of those willing to pay for their services.
Many low level transformations such as the above two examples would be not be that hard to implement, and some developers would regard them as useful. In some cases the behavior of the code as written would be required, and its transformed behavior would be surprising to the author, while in other cases the transformed behavior is what the developer would prefer if they were aware of it. Doesn’t it make sense to perform the transformations in those cases where the as-written behavior is least likely to be wanted?
Compilers already do things that are surprising to developers (often because the developer does not fully understand the language, many of which continue to grow in complexity). Creating the potential for more surprises is not that big a deal in the overall scheme of things.
Recent Comments