Archive
Estimating using a granular sequence of values
When asked for an estimate of the time needed to complete a task, should developers be free to choose any numeric value, or should they be restricted to selecting from a predefined set of values (e.g, the Fibonacci numbers, or T-shirt sizes)?
Allowing any value to be chosen would appear to provide the greatest flexibility to make an accurate estimate. However, estimating is an intrinsically uncertain process (i.e., the future is unknown), and it is done by people with varying degrees of experience (which might be used to help guide their prediction about the future).
Restricting the selection process to one of the values in a granular sequence of numbers has several benefits, including:
- being able to adjust the gaps between permitted values to match the likely level of uncertainty in the task effort, or the best accuracy resolution believed possible,
- reducing the psychological stress of making an estimate, by explicitly giving permission to ignore the smaller issues (because they are believed to require a total effort that is less than the sequence granularity),
- helping to maintain developer self-esteem, by providing a justification when an estimate turning out to be inaccurate, e.g., the granularity prevented a more accurate estimate being made.
Is there an optimal sequence of granular values to use when making task estimates for a project?
The answer to this question depends on what is attempting to be optimized.
Given how hard it is to get people to produce estimates, the first criterion for an optimal sequence has to be that people are willing to use it.
I have always been struck by the ritualistic way in which the Fibonacci sequence is described by those who use it to make estimates. Rituals are an effective technique used by groups to help maintain members’ adherence to group norms (one of which might be producing estimates).
A possible reason for the tendency to use round numbers might estimate-values is that this usage is common in other social interactions involving numeric values, e.g., when replying to a request for the time of day.
The use of round numbers, when developers have the option of selecting from a continuous range of values, is a developer imposed granular sequence. What form do these round number sequences take?
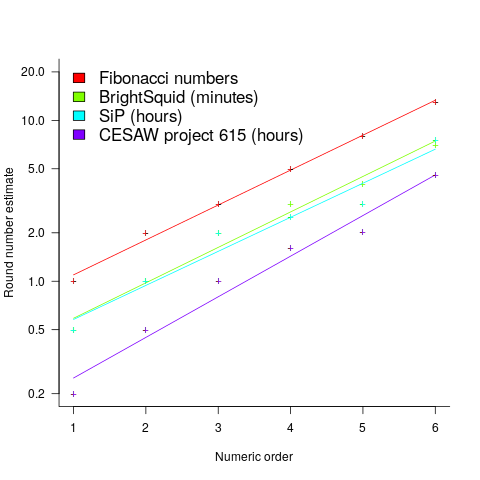
The plot below shows the values of each of the six most common round number estimates present in the BrightSquid, SiP, and CESAW (project 615) effort estimation data sets, plus the first six Fibonacci numbers (code+data):
The lines are fitted regression models having the form: 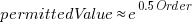 (there is a small variation in the value of the constant; the smallest value for project 615 was probably calculated rather than being human selected).
(there is a small variation in the value of the constant; the smallest value for project 615 was probably calculated rather than being human selected).
This plot shows a consistent pattern of use across multiple projects (I know of several projects that use Fibonacci numbers, but don’t have any publicly available data). Nothing is said about this pattern being (near) optimal in any sense.
The time unit of estimation for this data was minutes or hours. Would the equation have the same form if the time unit was days, would the constant still be around 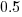 . I await the data needed to answer this question.
. I await the data needed to answer this question.
This brief analysis looked at granular sequences from the perspective of the distribution of estimates made. Perhaps it makes more sense to base a granular estimation sequence on the distribution of actual task effort. A topic for another post.
Fibonacci and JIT compilers
To maximize a compiler’s ability to generate high quality code many programming language standards do not specify the order in which the operands of a binary operator are evaluated. Most of the time the order of operand evaluation does not matter because all orders produce same final result. For instance in x + y the value of x may be obtained followed by obtaining the value of y and the two values added, alternatively the value of y may be obtained first followed by obtaining the value of x and the two values added; optimizers make use of local context information (e.g., holding one of the values in a register so it is immediately available for use in the evaluation of multiple instances of x) to work out which order produces the highest quality code.
If one of the operands is a function call that modifies the value of the other operand the result may depend on the order of evaluation. For instance, in:
int x; int set_x(void) { x=1; return 1; } int two_values(void) { x=0; return x + set_x(); } |
a left to right evaluation order of the return expression in two_values produces the value 1, while a right to left evaluation order produces the value 2. Every now and again developers accidentally write code that does something like this and are surprised to see program behavior change when they use different compiler options, a new version of the compiler or a different compiler (all things that can result in the order of evaluation changing for a given expression).
It is generally assumed that two calls to two_values within the same program will always produce the same answer, i.e., the decision on which order of evaluation to use is made at compile time and never changes while a program is running. Neither the C++ or C Standard requires that the evaluation order be fixed prior to program execution and use of a just-in-time compiler could result in the value returned by two_values alternating between 1 and 2. Some languages (e.g., Java) for which JIT compilers are expected to be used specify the exact order in which operands have to be evaluated.
One possible way of finding out whether a JIT compiler is being used for your C/C++ program is to test the values returned by two calls to two_values. A JIT compiler may, but is not required, to return different values on each call. Of course a decide-prior-to-execution C/C++ compiler does have the option of optimizing the following function to return true or false on the basis that the standard permits this behavior, but I would be very surprised to see this occur in practice:
bool Schrödinger(void) { return two_values() == two_values(); } |
The runtime variability offered by JIT compilers makes it possible to write a program whose output can be any value between  and
and 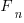 (the
(the  ‘th Fibonacci number, where
‘th Fibonacci number, where n is read from the input):
#include <stdio.h> int x; int set_x(int ret_val) { x=1; return ret_val; } int two_unspec(void) { x=0; return x + set_x(1); } int add_zero(val) { x=0; return val - x + set_x(0); } int fib(int fib_num) { if (fib_num > 3) return fib(fib_num-2) + add_zero(fib(fib_num-1)); else if (fib_num == 3) return two_unspec(); else return 1; } int main(void) { int n; scanf("%d", &n); printf("Fibonacci %d = %d\n", n, filb(n)); } |
The C-semantics tool will ‘execute’ this program and produce a list of the 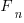 possible outputs (a PhD project under active development; the upper limit is currently around the 6th Fibonacci number which requires 11 hours and produces a 50G log file).
possible outputs (a PhD project under active development; the upper limit is currently around the 6th Fibonacci number which requires 11 hours and produces a 50G log file).
A decide-prior-to-execution compiler has a maximum choice of four possible outputs for a given input value and for a given executable the output produced by different input values will be perfectly correlated.
Recent Comments