Archive
Quality control in a zero cost of replication business
When a new manufacturing material becomes available, its use is often integrated with existing techniques, e.g., using scientific management techniques for software production.
Customers want reliable products, and companies that sell unreliable products don’t make money (and may even lose lots of money).
Quality assurance of manufactured products is a huge subject, and lots of techniques have been developed.
Needless to say, quality assurance techniques applied to the production of hardware are often touted (and sometimes applied) as the solution for improving the quality of software products (whatever quality is currently being defined as).
There is a fundamental difference between the production of hardware and software:
- Hardware is designed, a prototype made and this prototype refined until it is ready to go into production. Hardware production involves duplicating an existing product. The purpose of quality control for hardware production is ensuring that the created copies are close enough to identical to the original that they can be profitably sold. Industrial design has to take into account the practicalities of mass production, e.g., can this device be made at a low enough cost.
- Software involves the same design, prototype, refinement steps, in some form or another. However, the final product can be perfectly replicated at almost zero cost, e.g., downloadable file(s), burn a DVD, etc.
Software production is a once-off process, and applying techniques designed to ensure the consistency of a repetitive process don’t sound like a good idea. Software production is not at all like mass production (the build process comes closest to this form of production).
Sometimes people claim that software development does involve repetition, in that a tiny percentage of the possible source code constructs are used most of the time. The same is also true of human communications, in that a few words are used most of the time. Does the frequent use of a small number of words make speaking/writing a repetitive process in the way that manufacturing identical widgets is repetitive?
The virtually zero cost of replication (and distribution, via the internet, for many companies) does more than remove a major phase of the traditional manufacturing process. Zero cost of replication has a huge impact on the economics of quality control (assuming high quality is considered to be equivalent to high reliability, as measured by number of faults experienced by customers). In many markets it is commercially viable to ship software products that are believed to contain many mistakes, because the cost of fixing them is so very low; unlike the cost of hardware, which is non-trivial and involves shipping costs (if only for a replacement).
Zero defects is not an economically viable mantra for many software companies. When companies employ people to build the same set of items, day in day out, there is economic sense in having them meet together (e.g., quality circles) to discuss saving the company money, by reducing production defects.
Many software products have a short lifespan, source code has a brief and lonely existence, and many development projects are never shipped to paying customers.
In software development companies it makes economic sense for quality circles to discuss the minimum number of known problems they need to fix, before shipping a product.
Moving to the 12th cycle in fault prediction modeling
Most software fault prediction papers are based on a false assumption, i.e., a list of dates when a fault was first experienced, by a program, contains enough information to build a model that has a connection to reality. A count of faults that have been experienced twice is also required, to fit a basic model that has some mathematical connection to reality.
I had thought that people had moved on from writing papers that fitted yet more complicated equations to one of the regularly used data sets. No, it seems they have just switched to publishing someplace they have not been seen before.
Table 1 lists the every increasing number of cycles within cycles; the new model is proposed as the 12th refinement (the table is a summary, lots of forks have been proposed over the years). I have this sinking feeling there is another paper in the works, one that ‘benchmarks’ the new equation using a collection of the other regular characters data sets that appear in papers of this kind.
Fitting an equation to data of first experience of a fault is little better than fitting noise.
As Planck famously said, science advances one funeral at a time.
Programs spent a lot of time repeating themselves
Inexperienced software developers are always surprised that programs used by lots of people can contain many apparently non-trivial faults and yet continue to operate satisfactorily; experienced developers become familiar with this state of affairs and tend to shrug their shoulders. I have previously written about how software is remarkably fault tolerant. I think this fault tolerance is telling us something important about the characteristics of software and while I have some ideas about what it might be I don’t yet have a good handle (or data) on what is going on to lay out my argument.
In this article I’m going to talk about another characteristic of program execution which I think is connected to program fault tolerance and is also very surprising.
Software differs from hardware in that for a given set of inputs a program will always produce the same output, it will not wear out like hardware and eventually do something different (to simplify things I’m ignoring the possible consequences of uninitialized variables and treating any timing dependencies as part of the input set). So for a fault to be observed different input is required (assuming one exists and none appeared for the first input set).
I used to assume that during a program’s execution the basic cpu operations (e.g., binary arithmetic and bitwise operations) processed a huge number of different combinations of input values (e.g., there are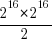 
combinations of input value for a 16-bit add operation) and was very surprised to find out this is not the case. For many programs around 80% of all executed instructions are repeat instructions, that is a given instruction, such as add, operates on the same combinations of input values that it has previously operated on (while executing the program) to generate an output value that is identical to the one previously generated from these input values. If we count the number of static instructions in the program (i.e., the number of assembly instructions in a listing of the disassembled executable program) then 20% of them account for 90% of the repeated instructions; so a small amount of code (i.e., 20%) is not only responsible for most dynamically executed instructions but around 72% (i.e., 80%*90%) of these instructions repeat previous computations. If a large percentage of a what goes on internally within a program is repetition is it any surprise that once it works for a reasonable set of inputs it will probably work on other inputs?
Hang on you say, perhaps the percentage of repeat instructions is very high for a given set of external input values (e.g., a file to compress, compile or display as a jpeg) but there is a lot of variation in the set of repeat instructions between different external inputs. Measurements suggest this is not the case, with around 20% of dynamic instructions having input values that can be traced to external program input (12-30% come from globally initialized variables and the rest are generated internally).
There is a technical detail that reduces the repeat instruction percentages given about by a factor of two; researchers always like to give the most favorable numbers and for this discussion we need to make a distinction between local repetition which counts one instruction and its inputs/outputs at a particular point in the code and global repetition which counts all instructions of a given kind irrespective of where they occur in the code. A discussion of fault behavior needs to look at local repetition, not global repetition; there is a factor of two difference in the dynamic percentage and some reduction in the percentage of static instructions involved.
Sometimes the term redundant computation is used, as if the cpu should remember what happened last time it executed an instruction with a particular set of inputs and reuse the answer it got last time. Researchers have proposed caching the results of executing an instruction with a given set of input values and speeding things up or saving power by reusing previous results rather than recalculating them (a possible speedup of 13% on SPEC95 is claimed for a reuse buffer containing 4096 entries).
So a small percentage of the instructions in a program account for most of the execution time (a generally known characteristic) and around 30% of the executed instructions operate on input values they have processed before to produce output they have produced before (to the extent that a cache containing a few thousand entries is big enough to hold the a large percentage of the duplicates). If encountering a new fault requires different execution behavior to occur then having a large percentage of a program always doing the same thing (i.e., same input values same output value) will have a significant impact on the likelihood of encountering a fault. Part of the reason programs are fault tolerant is because external input values don’t have a big an impact on program behavior as we might have thought.
Researchers have also investigated repeats involving units larger than one instruction, such as sub-blocks (a sequence of instructions smaller than a basic block) and even complete functions or just the mathematical ones.
The raw data is obtained using cpu simulators to monitor programs as they are executed, logging the values read as input by an instruction and the value generated as output (in most cases the values are read from registers and written to a register). A single study might log billions of instructions from the SPEC benchmark.
Impact of hardware characteristics on detectable fault behavior
Preface. This is the first of what I hope will be many posts analysing experimental data, that will eventually end up in my empirical software engineering with R book (this experiment was chosen because it happens to be the one I am currently working on; having just switched to using Asciidoc I have a backlog of editing to do on previously written analysis, also I have to figure out a way to fix [bracketed words]).
Don’t worry if you don’t know anything about the statistics used. I am aiming to provide information to meet the needs of two audiences (whether or not I fail on both counts remains to be seen):
- Those who want to some idea of what facts are known about a particular software engineering topic. Hopefully reading the introduction+conclusion will enable these readers to form an opinion about the current state of knowledge (taking my statistical analysis on trust).
- Those who are looking for ideas that can be used to analyse a problem they are trying to solve. Hopefully, somewhere among my many analyses will be something that looks like it could be applied to the reader’s problem and motivates them to go off and learn something about the statistics (if they are not already familiar with it; once written the book will obviously help out here).
Forward. The following analysis produces a negative result, something that happens a lot in experiments in all fields of research. It has been included to illustrate the importance of checking the statistical power of an experiment, i.e., how likely the experiment will detect an effect if one is present; it is very easy to fall into the trap of thinking that because lots of tests were done any effect that exists will be detected.
The authors ran an interesting experiment which as far as I know is the only published empirical analysis of intermittent software faults (please let me know if you are aware of other work) and made some mistakes in their statistical analysis. I have made plenty of mistakes in experiments I have run, some of which have found there way into the published write up. The key attribute of an experimentalist is to learn and move on.
A fault does not always noticeably change the behavior of a program when it is executed, apparently correct program execution can occur in the presence of serious faults.
A study by Syed, Robinson and Williams <book Syed_10> investigated how the number of noticeable failures caused by known faults in Mozilla’s Firefox browser varied with processor speed, system memory, hard disc size and system load. A total of 11 known faults causing intermittent failure were selected and nine different hardware configurations were selected. The conditions required to exhibit each fault were replicated and Firefox was executed 10 times for each of hardware configuration, counting the number of noticeable program failures; the seven faults and nine hardware configurations listed in the table below generated a total of 10*7*9 = 630 different executions (four faults either always or never resulted in an observed failure during the 10 runs).
Data
The following table contains the observed number of failures of Firefox for the given fault number when run on the specified hardware configuration.
| Mhz-Mb-Gb | 124750 | 380417 | 410075 | 396863 | 494116 | 264562 | 332330 |
|---|---|---|---|---|---|---|---|
|
667-128-2.5 |
4 |
10 |
6 |
5 |
2 |
3 |
5 |
|
667-256-10 |
4 |
8 |
8 |
6 |
4 |
3 |
8 |
|
667-1000-2.5 |
4 |
7 |
3 |
4 |
3 |
1 |
8 |
|
1000-128-10 |
3 |
10 |
3 |
6 |
0 |
1 |
1 |
|
1000-256-2.5 |
3 |
9 |
0 |
6 |
0 |
1 |
2 |
|
1000-1000-10 |
2 |
9 |
4 |
5 |
0 |
0 |
1 |
|
2000-128-2.5 |
0 |
10 |
5 |
6 |
0 |
0 |
0 |
|
2000-256-10 |
2 |
8 |
5 |
7 |
0 |
0 |
0 |
|
2000-1000-10 |
1 |
7 |
3 |
5 |
0 |
0 |
0 |
Predictions made in advance
There is no prior theory suggesting how the selected hardware characteristics might influence the outcome from this experiment. The analysis is based on searching for a pattern in the results and so the significance level needs to be adjusted to take account of the number of possible patterns that could exist (e.g., using the [Bonferroni correction]).
If we simplify the failure counts by labelling them as one of Low/Medium/High, then there are two arrangements of the failure counts (i.e., low/medium/high and high/medium/low) that would result in a strong correlation for cpu_speed, two arrangements for memory and two for disc size; a total of 6 combinations that would result in a strong correlation being found.
The [Bonferroni correction] adjusts the significance level by dividing by the number of tests, in this case 0.05/6 = 0.0083.
If the failure counts occurred in a random order what is the probability of a strong correlation between failure count and one of the hardware attributes being found? Based on the Low/Medium/High labelling scheme there are 9!/(3! 3! 3!) = 1680 combinations of these counts over 9 slots, giving a 1 in 1680/6 = 280 chance of purely random behavior producing a strong correlation.
The experiment investigated the characteristics of 11 faults. If there is a 1 in 280 chance of finding a strong correlation when analyzing one fault there is approximately a 1 in 24 chance of finding at least one strong correlation when analysing 11 different faults.
Response variable
The response variable takes the form of a proportion whose value varies between 0 and 1, the number of failures out of 10 executions.
Applicable techniques
The following techniques might be used to analyse this data:
- [Factorial design]. This is a way of organizing experiment configurations that is designed to extract the most information for the total number of program runs made. It would be inefficient not to use the results from some hardware configurations just because they are not needed in the factorial design and no results are available for some configurations required by a factorial design (or a [Plackett-Burman] design).
-
Fitting the data using a linear model. A standard linear model, created using R’s lm function, would not be appropriate because of the following two problems:
- this kind of model is likely to make predictions that fall outside the range 0 to 1, something that cannot happen for proportional data,
- this approach assumes that the variance is constant across measurements and unless the proportions involved are very close to each other this requirement will not be met ([proportional data] from a [binomial distribution] has variance p(1-p)).
However, a generalised linear model would not suffer from these problems. There are several [link functions] that could be used:
- the Poisson distribution, is widely used for modelling faults but requires that the mean and variance have the same value, a property that does not apply to proportional data.
- the Binomial distribution, can handle data having the characteristics present here.
The proportional data is specified in the call to the glm function by having the response variable contain two columns, one containing the number of failures (that is what is being predicted in this case) and the other the number of non-failures. The code looks something like the following (see complete example and data):
y=cbind(fail_count, 10-fail_count) glm(y ~ cpu_speed+memory+disk_size, data=ff_data, family=binomial) |
In this kind of GLM it is assumed that the [residual deviance] is the same as the [residual degrees of freedom]. If the residual deviance is greater than the residual degrees of freedom then [overdispersion] has occurred, which happens for fault 380417. To handle overdispersion the family needs to be changed from binomial to quasibinomial, which in the case of fault 380417 changes the p-value of the fit from 0.0348 to 0.0749.
The analysis of each fault finds that only one of them, 332330, has a significance level within the specified acceptable bounds; this has a negative correlation with CPU speed (i.e., observed failures decrease with clock speed).
With only one faults found to have any significant hardware configuration effects we have to ask about the probability of this experiment finding an effect if one was present.
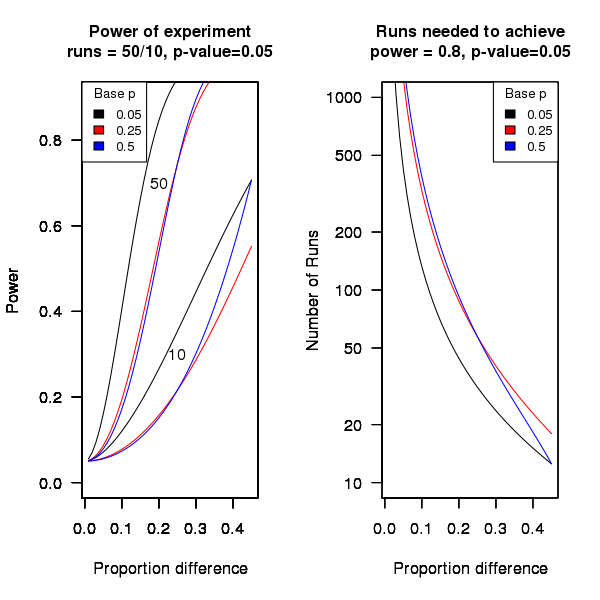
An analysis of the [statistical power] of an experiment investigating the difference between proportions for two hardware configurations (i.e., the percentage of observed failures) needs to know the value of those proportions, the number of runs (10 in this case) and the desired p-value (0.05); to simplify things the plot below is based on using the value of the lowest proportion and the difference between it and the higher proportion. The left plot shows the power achieved (y-axis) there does exist a given difference in proportions (x-axis), the three lowest proportions of 0.05, 0.25 and 0.5 are shown (the result is symmetric about 0.5 and so the plot for 0.75 and 0.95 would be the same as 0.25 and 0.05 respectively), and where there were 10 and 50 runs involving the same fault case.
It can be seen that unless a change in the hardware configuration causes a large change in the number of visible failures then the chance of a difference being detected in results from 10 runs is well below 0.5 (i.e., less than a 50% chance of detecting a difference at a p-value of 0.05 or better).
The right plot in the figure gives the number of runs that need to be made to have a 80% chance of detecting, between two different hardware configurations, the difference in proportion listed on the x-axis, at a significance of 0.05.
It can be seen that if hardware charactersitics account for only 10% of the difference in failure rate over 100 runs would be needed to detect it.
Conclusion
Faults in Firefox that caused intermittent failures were investigated looking for a correlation with system cpu speed, memory or disc size. One fault showed a strong correlation with cpu speed (there is a 1 in 24 chance that one of the investigated faults would have some kind of strong correlation). This experiment may not have found a significant correlation between observed failure rate and hardware configuration because the number of separate runs for each fault (i.e., 10) had [low power].
A fault in the C Standard or existing compilers?
Software is not the only entity that can contain faults. The requirements listed in a specification are usually considered to be correct, almost by definition. Of course the users of software implementing a specification may be unhappy with the behavior specified and wish that some alternative behavior occurred. A cut and dried fault occurs when two requirements conflict with each other.
The C Standard can be read as a specification for how C compilers should behave. Despite over 80 man years of effort and the continued scrutiny of developers over 20 years, faults continue to be uncovered. The latest potential fault (it is possible that the fault actually occurs in many existing compilers rather than the C Standard) was brought to my attention by Al Viro, one of the Sparse developers.
The issue involved the following code (which I believe the standard considers to be strictly conforming, but all the compilers I have tried disagree):
int (*f(int x))[sizeof x]; // A prototype declaration int (*g(int y))[sizeof y] // A function definition { return 0; } |
These function declarations are unusual in that their return type is a pointer to an array of integers, a type rarely encountered in this context (the original question involved a return type of pointer to function returning … and was more complicated).
The specific issue was the scope of the parameter (i.e., x and y), is the declaration still in scope at the point that the second occurrence of the identifier is encountered?
As a principle I think that the behavior, whatever it turns out to be, should be the same in both cases (neither the C standard or its rationale state such a principle).
Taking the function prototype case first:
The scope of the parameter x “… terminates at the end of the function declarator.” (sentence 409).
and does function prototype scope include the return type (the syntax calls the particular construct a declarator and there are at least two of them, one nested inside the other, in a function prototype declaration)?
Sentence 1592 says Yes, but sentence 279 and 1845 say No.
None of these references are normative references (standardize for definitive).
Moving on to the function definition case:
Where does the scope of the parameter x begin (sentence 418)?
“… scope that begins just after the completion of its declarator.”
and where does the scope end (sentence 408)?
“… which terminates at the end of the associated block.”
and what happens between the beginning and ending of the scope (sentence 412)?
“Within the inner scope, the identifier designates the entity declared in the inner scope;”
This looks very straight forward, there are no ‘gaps’ in the scope of the parameter definition appearing in a function definition. Consistency with the corresponding function prototype case requires that function declarator be interpreted to include the return type.
There is a related discussion involving a previous Defect Report 345 submitted a while ago.
The problem is that many existing compilers do not treat parameter scope in this way. They operate as-if there was a ‘gap’ in the parameter scope of function definition (probably because the code implementing this functionality is shared with that implementing function prototypes, which have been interpreted to not include the return type).
What happens next? Probably lots of discussion on the C Standard email reflector. Possible outcomes include somebody finding wording that requires a ‘gap’ in the scope of parameters in function definitions, it agreed that such a gap ought to be specified by the standard (because this is how existing code behaves because this is how compilers operate), or that the standard is correct as is and any compiler that behaves differently needs to be fixed.
Recent Comments