Archive
Perturbed expressions may ‘recover’
This week I have been investigating the impact of perturbing the evaluation of random floating-point expressions. In particular, the impact of adding 1 (and larger values) at a random point in an expression containing many binary operators (simply some combination of add/multiply).
What mechanisms make it possible for the evaluation of an expression to be unchanged by a perturbation of +1.0 (and much larger values)? There are two possible mechanisms:
- the evaluated value at the perturbation point is ‘watered down’ by subsequent operations, such that the original perturbed value makes no contribution to the final result. For instance, the IEEE single precision float mantissa is capable of representing 6-significant digits; starting with, say, the value
0.23, perturbing by adding1.0gives1.23, followed by a sequence of many multiplications by values between zero and one could produce, say, the value6.7e-8, which when added to, say,0.45, gives0.45, i.e., the perturbed value is too small to affect the result of the add, - the perturbed branch of the expression evaluation is eventually multiplied by zero (either because the evaluation of the other branch produces zero, or the operand happens to be zero). The exponent of an IEEE single precision float can represent values as small as
1e-38, before underflowing to zero (ignoring subnormals); something that is likely to require many more multiplies than required to lose 6-significant digits.
The impact of a perturbation disappears when its value is involved in a sufficiently long sequence of repeated multiplications.
The probability that the evaluation of a sequence of 
multiplications of random values uniformly distributed between zero and one produces a result less than 
is given by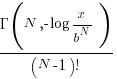 
, where 
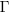is the incomplete gamma function, and 
is the upper bounds (1 in our case). The plot below shows this cumulative distribution function for various (code):
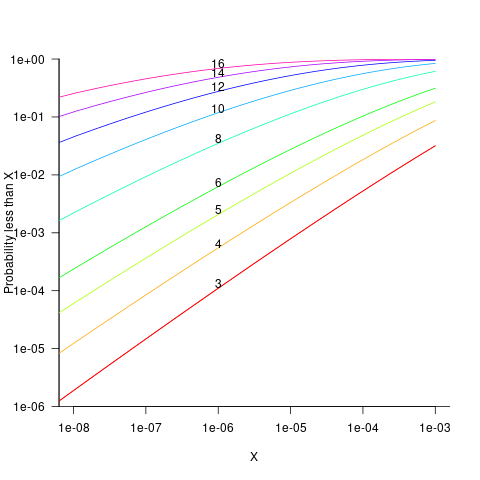
Looking at this plot, a sequence of 10 multiplications has around a 1-in-10 chance of evaluating to a value less than 1e-6.
In practice, the presence of add operations will increase the range of operands values to be greater than one. The expected distribution of result values for expressions containing various percentages of add/multiply operators is covered in an earlier post.
The probability that the evaluation of an expression involves a sequence of multiplications depends on the percentage of multiply operators it contains, and the shape of the expression tree. The average number of binary operator evaluations in a path from leaf to root node in a randomly generated tree of operands is proportional to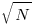 
.
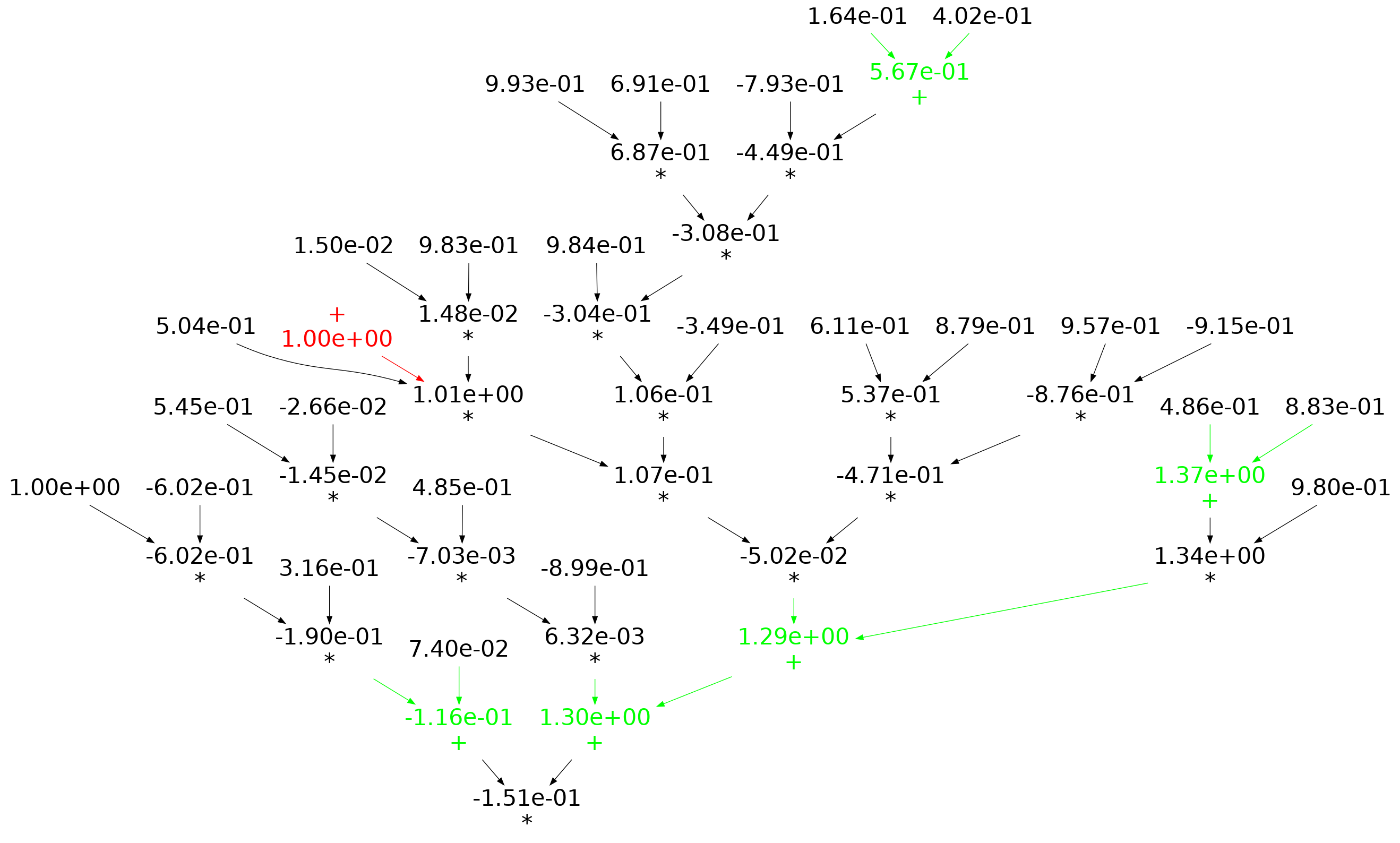
When an expression has a ‘bushy’ balanced form, there are many relatively distinct evaluation paths, the expected number of operations along a path is proportional to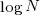 
. The plot below shows a randomly generated ‘bushy’ expression tree containing 25 binary operators, with 80% multiply, and randomly selected values (perturbation in red, additions in green; code+data):
When an expression has a ‘tall’ form, there is one long evaluation path, with a few short paths hanging off it, the expected number of operations along the long path is proportional to . The plot below shows a randomly generated ‘tall’ expression tree containing 25 binary operators, with 80% multiply, and randomly selected values (perturbation in red, additions in green; code+data):
If, one by one, the result of every operator in an expression is systematically perturbed (by adding some value to it), it is known that in some cases the value of the perturbed expression is the same as the original.
The following results were obtained by generating 200 random C expressions containing some percentage of add/multiply, some number of operands (i.e., 25, 50, 75, 100, 150), one-by-one perturbing every operator in every expression, and comparing the perturbed result value to the original value. This process was repeated 200 times, each time randomly selecting operand values from a uniform distribution between -1 and 1. The perturbation values used were: 1e0, 1e2, 1e4, 1e8, 1e16. A 32-bit float type was used throughout.
Depending on the shape of the expression tree, with 80% multiplications and 100 operands, the fraction of perturbed expressions returning an unchanged value can vary from 1% to 40%.
The regression model fitted to the fraction of unchanged expressions contains lots of interactions (the simple version is that the fraction unchanged increases with more multiplications, decreases as the log of the perturbation value, the square root of the number of operands is involved; code+data):
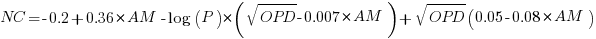
where: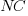 
is the fraction of perturbed expressions returning the original value, 
the percentage of add operators (not multiply), 
the number of operands in the expression, and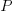 
the perturbation value.
There is a strong interaction with the shape of the expression tree, but I have not found a way of integrating this into the model.
The following plot shows the fraction of expressions unchanged by adding one, as the perturbation point moves up a tall tree, x-axis, for expressions containing 50 and 100 operands, and various percentages of multiplications (code+data):
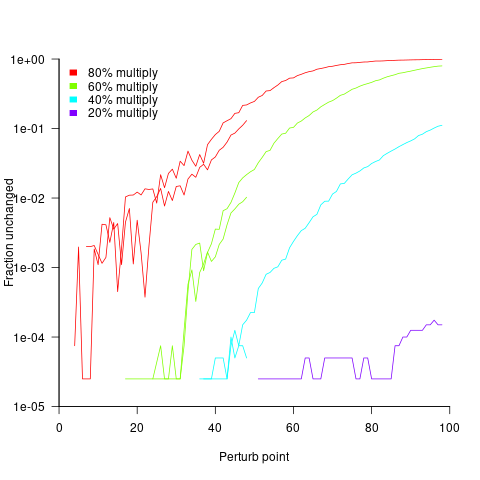
No attempt was made to count the number of expression evaluations where the perturbed value was eventually multiplied by zero (the second bullet point discussed at the start).
Percolation of the impact of coding mistakes through a program
Programs containing serious coding mistakes can sometimes work surprisingly well. Experienced developers invariably have a story to tell about a program in production use that contained a coding mistake so bad, that it should have prevented the program producing any reliably output. My story relates to a Z80 cpu emulator I had written, which was successfully booting/running CP/M and several applications. One application was sometimes behaving erratically. I eventually traced the problem to the implementation of one of the add instructions (there are 13 special cases), which had been cut/pasted from the implementation of the corresponding subtract instruction, except that I had forgotten to change the result calculation from using a subtract to using an add, i.e., the instruction was performing a subtract, not an add. I was flabbergasted that so much emulated code appeared to be working in the presence of what to me was a crippling coding mistake.
There have been a handful of studies investigating the ability of programs containing coding mistakes to function correctly, or at least well enough to be usable.
- The earliest paper I have found is from 2005; Rinard, Cadar and Nguyen changed the termination condition of 326
for-loopsin the Pine email client, with<becoming<=, and>becoming>=. While the resulting program exhibited obvious anomalies, the researchers were able to use it to send and receive email, - a study by Danglot, Preux, Baudry and Monperrus investigated the propagation of single perturbations in 10 short Java programs (42 to 568 LOC, perturbed by adding/subtracting 1 from an expression somewhere in the code). The plot below shows the likelihood that a perturbation at some point in the code will have no impact on the output; code+data,
- a study by Cho of the impact of soft errors (i.e., radiation induced bit-flips) found that over 80% of bit-flips had no detectable impact on program behavior.
This week I attended the 63rd CREST Open Workshop; the topic was genetic improvement of software, i.e., GI randomly combines members of a population of programs, only keeping the children that pass some fitness test, rinses and repeats until one or more programs reach some acceptance threshold.
The GI community recently discovered that program output is often unaffected by a small perturbation to program execution, e.g., randomly adding one to the result of a binary operation.
A study by Langdon, Al-Subaihin and Clark tracked the effect of perturbations in the evaluation of an expression tree. The expression trees were created using genetic programming, with the fitness function being the difference between the value obtained by evaluating the expression tree and a sixth order polynomial. The binary operators in the expression tree were multiply and addition, with the leaf node value, x, taking a value between -0.97789 and 0.979541; the trees were a lot deeper than the one below, containing between 8.9k and 863k nodes/leafs, with tree depth varying from 121 to 5,103.
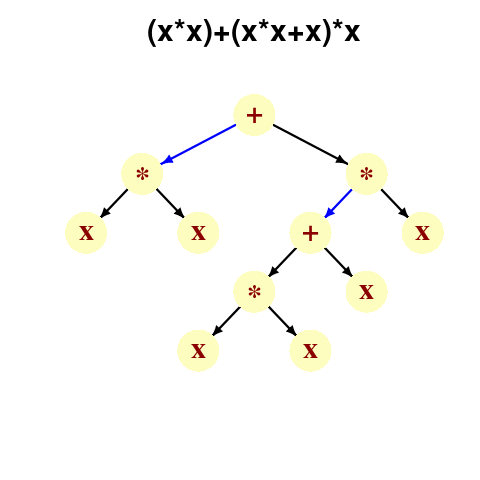
During the evaluation of an expression tree the result of one of the multiply/add operations was perturbed by adding one to its value. The subsequent evaluation of the remainder of the expression tree was tracked, comparing original/perturbed calculated values until either the root node was reached (and the final result was different), or the original/perturbed subtree result values synchronized, i.e., became the same. The distance, in nodes, between perturbation and value synchronization was recorded.
In all, ten expression trees were created, and each node in every tree was perturbed once per run; there were 10 runs using 10 different values of x.
The plot below shows results from two expression trees (different colors). Each point is the distance before original/perturbed values synchronised (for those cases where this happened) against the number of runs having this distance (for the same tree; code+data, and thanks to Bill for explaining things):
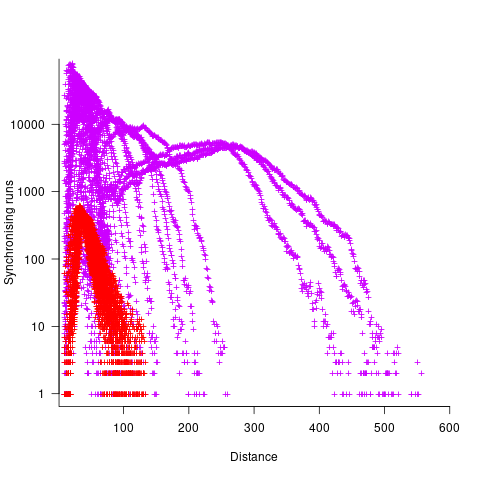
For the larger tree, there is a distinct pattern for each of the ten input values, x. This shows that synchronisation distance can be affected by the input value (which is to be expected). Perhaps this pattern is not present in the smaller tree, or the points are too close together to see it.
The opportunities available to a perturbation for travelling some distance depends on the size and characteristics of the expression tree, with a large thin tree providing more opportunities for longer distance travel than a large bushy tree.
It will take some well thought through experiments to unpick the contributions made by the tree characteristics, problem characteristics, and the prevalence of binary operators unlikely to be affected by small changes to their operand value, e.g., there is roughly a 50% chance that a relational comparison will be unaffected by a small change to one of its operands.
If you know of any other studies investigating coding mistake percolation, please let me know.
Giving engineers the freedom to create a customer lock-in Cloud
The Cloud looks like the next dominant platform for hosting applications.
What can a Cloud vendor do to lock customers in to their fluffy part of the sky?
I think that Microsoft showed the way with their network server protocols (in my view this occurred because of the way things evolved, not though any cunning plan for world domination). The EU/Microsoft judgment required Microsoft to document and license their server protocols; the purpose was to allow third-parties to product Microsoft server plug-compatible products. I was an advisor to the Monitoring trustee entrusted with monitoring Microsoft’s compliance and got to spend over a year making sure the documents could be implemented.
Once most the protocol documents were available in a reasonably presentable state (Microsoft originally considered the source code to be the documentation and even offered it to the EU commission to satisfy the documentation requirement; they eventually hire a team of several hundred to produce prose specifications), two very large hurdles to third party implementation became apparent:
- the protocols were a tangled mess of interdependencies; 100% compatibility required implementing all of them (a huge upfront cost),
- the specification of the error behavior (i.e., what happens when something goes wrong) was minimal, e.g., when something unexpected occurs one of the errors in
windows.his returned (when I last checked, 10 years ago, this file contained over 30,000 identifiers).
Third party plugins for Microsoft server protocols are not economically viable (which is why I think Microsoft decided to make the documents public, they had nothing to loose and could claim to be open).
A dominant cloud provider has the benefit of size, they have a huge good-enough code base. A nimbler, smaller, competitor will be looking for ways to attract customers by offering a better service in some area, which means finding a smaller, stand-alone, niche where they can add value. Widespread use of Open Source means everybody gets to see and use most of the code. The way to stop smaller competitors gaining a foothold is to make sure that the code hangs together as a whole, with no relatively stand-alone components that can be easily replaced. Mutual interdependencies and complexity creates a huge barrier to new market entrants and is in the best interests of dominant vendors (yes it creates extra costs for them, but these are the price for detering competitors).
Engineers will create intendependencies between components and think nothing of it; who does not like easy solutions to problems and this one dependency will not hurt will it? Taking the long term view, and stopping engineers taking short cuts for short term gain, requires a lot of effort; who could fault a Cloud vendor for allowing mutual interdependencies and complexity to accumulate over time.
Error handling is a very important topic that rarely gets the attention it deserves, nobody likes to talk about the situation where things go wrong. Error handling is the iceberg of application development, while the code is often very mundane, its sheer volume (it can be 90% of the code in an application) creates a huge lock-in. The circumstances under which a system handles raises an error and the feasible recovery paths are rarely documented in any detail, it is something that developers working at the coal face learn by trial and error.
Any vendor looking to poach customers first needs to make sure they don’t raise any errors that the existing application does not handle and second any errors they do raise need to be solvable using the known recovery paths. Even if there is error handling information available to enable third-parties to duplicate responses, the requirement to duplicate severely hampers any attempt to improve on what already exists (apart from not raising the errors in the first place).
To create an environment for customer lock-in, Cloud vendors need to encourage engineers to keep doing what engineers love to do: adding new features and not worrying about existing spaghetti code.
Brief history of syntax error recovery
Good recovery from syntax errors encountered during compilation is hard to achieve. The two most common strategies are to insert one or more tokens or to delete one or more tokens. Make the wrong decision and a second syntax error will occur, often leading to another and soon the developer is flooded by a nonsensical list of error messages. Compiler writers soon learn that their first priority is ensuring that syntax error recovery does not result in lots of cascading errors. In languages that use a delimiter to indicate end of statement/declaration, usually a semicolon, the error recovery strategy of deleting all tokens until this delimiter is next encountered is remarkably effective.
The era of very good syntax error recovery was the 1970s and early 1980s. Developers working on mainframes might only be able to achieve one or two compilations per day on a batch oriented mainframe and they were not happy if a misplaced comma or space resulted in a whole day being wasted. Most compilers were rented for lots of money and customer demand resulted in some very fancy error recovery strategies.
Borland’s Turbo Pascal had a very different approach to handling errors in code, it stopped processing the source as soon as one was detected. The combination of amazing compilation rates and an interactive environment (MS-DOS running on the machine in front of the developer) made this approach hugely attractive.
To a large extent syntax error recovery has been driven by the methods commonly used to write parsers. Many compilers use a table driven approach to syntax analysis with the tables being generated by parser generator tools such as Yacc. During the 1970s and 80s a lot of the research on parser generators was aimed at reducing the size of the generated tables. A table of 10k bytes was a significant percentage of available storage for machines that supported a maximum of 64k of memory. Some parser table compression techniques involve assuming the default behavior and then handling any special cases when these defaults are found not to apply, but one consequence is that context information needed for good error recovery is often not available when an error is detected. The last major release of Yacc from AT&T in the early 1990s managed another reduction in table size, just as typical storage sizes were getting into the ten of megabytes, but at the expense of increasing the difficulty of doing good error recovery.
While there are still some application areas where the amount of storage occupied by parser tables is still a big issue, e.g., the embedded market, developers of parser generators such as Bison ought to start addressing the needs of users wanting to do good error recovery and who are willing to accept larger tables.
I am pleased to see that the LLVM project is making an effort to provide good syntax error recovery. A frustrating barrier to providing better error recovery is lack of information on the kinds of syntax errors commonly made by developers; there are a few papers and reports containing small scale measurements of errors made by students. Perhaps the LLVM developers will provide a mechanism for automatically collecting compilation errors and providing users with the option to send the results to the LLVM project.
One of my favorite syntax error recovery techniques (implemented in a PL/1 mainframe compiler; I have never been able to justify implementing it on any project I worked on) is the following:
// Use of an undeclared identifier is a syntax error in C and some other // languages, while in other languages it is a semantic error. // no identifier with name result visible here { int result; ... result=... ... } ... calc=result*2; // Error reported by most compilers is use of an undeclared variable |
The ‘real’ error is probably the misplaced closing bracket. Other possibilities include result being a misspelled version of another variable or the assignment to calc being in the wrong place.
There seems to be a trend over the last 20 years to create languages that require more and more semantic information during parsing. Deciphering a syntax error today can involve a lot more than figuring out which surrounding tokens have been omitted or misplaced, information on which types are in scope and visible (oh for the days when that meant the same thing) and where they might be found in the umpteen thousand lines of included source has to be distilled and presented to the developer in a helpful message.
For a long time compilers have primarily been benchmarked on the quality of their code. With every diminishing returns from improved optimization, the increasing complexity of languages and the increasing volume of header code pulled in during compilation perhaps the quality of syntax error recovery will grow in importance.
Recent Comments