Archive
Learning General relativity at a rudimentary mathematical level
For the longest time, I have wanted to have an understanding of Einstein’s theory of General relativity at a rudimentary mathematical level. Because General relativity has never been a mainstream topic in undergraduate physics, there are almost no books at this level. Also, the mathematics of General relativity is based on tensor calculus, which until recently was rarely used in engineering and non-relativistic physics; market size explains the lack of non-specialist books on the subject.
The Theoretical Minimum is a book series that aims to teach everything required to gain a basic understanding of various areas of modern physics. The primary author of the books is Leonard Susskind.
At the start of this year, “General Relativity: The Theoretical Minimum” by Susskind and Cabannes was published as a paperback (i.e., convenient for reading on the London Underground), and over the last two months I have been slowly working my way through it.
At the start of this week, I discovered Eddie Boyes’ YouTube series on General relativity.
An understanding of General relativity requires an understanding of Tensor calculus, which in turn requires understanding the contravariant and covariant components of a vector. In the Cartesian coordinates system, which pervades undergraduate physics, the axes are at right angles and the measurement units are constant. The covariant component of a vector is the same as the contravariant component.
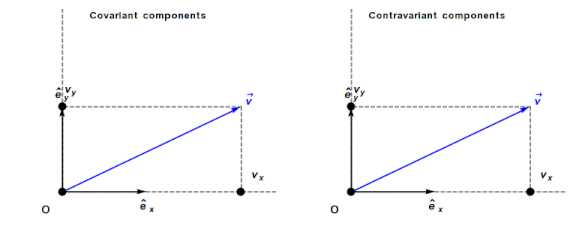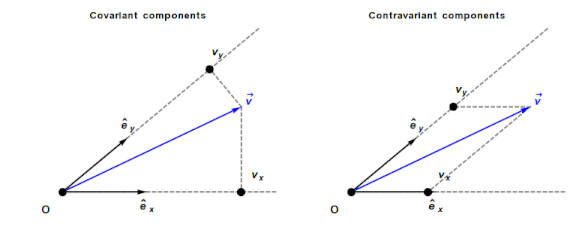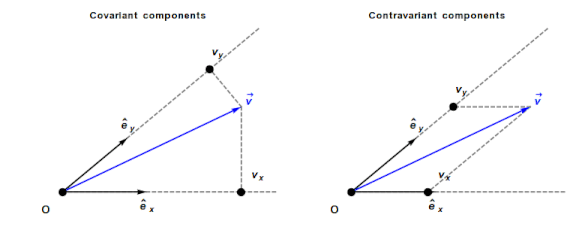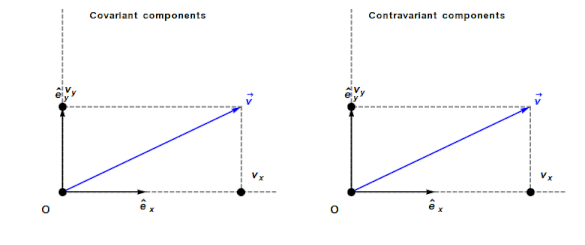
Contravariant/covariant vectors are different when the axes are not at right angles, as the plot below (from Wikipedia), shows. Choosing one component of the blue vector, the 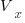 component of its contravariant vector is measured by drawing a line parallel to the y-axis (on right), while the
component of its contravariant vector is measured by drawing a line parallel to the y-axis (on right), while the 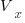 component of its covariant vector is found by drawing a line perpendicular to the x-axis (on left). The plot below shows how the measurements of each component vary as the angle between the x/y axes varies:
component of its covariant vector is found by drawing a line perpendicular to the x-axis (on left). The plot below shows how the measurements of each component vary as the angle between the x/y axes varies:
Susskind’s definition of covariant vectors is a differential equation, which might be enough for some people, but not me. Boyes gives a very clear description (he does labour points, and I watched at 1.75 speed).
There are other places where I found Boyes’ explanation to be clearer, and a few where I preferred Susskind. I would recommend both.
What complicates the use of Tensor calculus is the multiplicity of terms in an equation. In 3-dimensional Cartesian coordinates there are three variables x/y/z, while in 3-dimensional Tensor calculus there are nine variables (the coordinate system can produce an interaction between any axis and another one). The equation for the proper acceleration of an object, written using the Einstein summation convention (there is a summation over the repeated indexes, 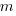 ,
,  ,
, 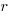 ) is:
) is: 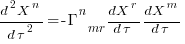 . In three dimensions, there would be three equations (i.e.,
. In three dimensions, there would be three equations (i.e., 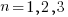 ), each with nine terms on the right, for
), each with nine terms on the right, for 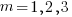 ,
, 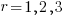 ;
; 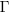 is the Christoffel symbol which calculates the unit distance for a location in space (in Cartesian coordinates this simplifies down to what we all learned in school); the superscripts denote contravariant components, and the subscripts denote covariant components:
is the Christoffel symbol which calculates the unit distance for a location in space (in Cartesian coordinates this simplifies down to what we all learned in school); the superscripts denote contravariant components, and the subscripts denote covariant components:
How did Einstein derive his field equation, 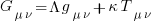 , of General relativity?
, of General relativity?
I had known of the equivalence principle, that the force experienced by an accelerating observer (e.g., travelling in an elevator) is indistinguishable from the force of gravity, but had not appreciated how this principle played an integral part in the derivation of the equations for the force experienced in a gravitational field.
The derivation is based on asking about the trajectory of a rocket accelerating at a constant rate in a flat space-time (allowing Cartesian coordinates to be used). If a stationary observer on the ground tracks the rocket from when it starts with zero velocity and then constantly accelerates in a straight line for a very long time, how will the velocity and distance of the rocket (from the observer) change over time? From the ground-based observer’s perspective, the rocket’s velocity will get closer and closer to the speed of light; Special relativity prevents it exceeding the speed of light. The distance travelled by the rocket over time, as tracked by the ground-based observer, will be seen to be fitted by a hyperbolic equation. This analysis is used to justify the use of hyperbolic geometric as a coordinate system for dealing with gravity.
A hyperbolic metric space was not enough for Einstein to derive his equations. He also assumed conservation of various quantities, and appears to have included some idealism about how the Universe ought to operate.
Special relativity predicts some very surprising behaviors, such as of time dilation. What very surprising behaviours does General relativity predict?
The bending of light by gravity is often cited as an example of a prediction by General relativity. However, bending is predicted my Newtonian mechanics, but the amount is half that predicted by General relativity.
While Black holes get a lot of public attention, and are discussion time by Susskind and Boyes, General relativity is not needed to make the prediction that that gravitational attraction of a sufficiently massive body will be greater than the speed of light.
General relativity deals with accelerating frames of reference (gravity or rocket ships). Both Susskind and Boyes discuss some version of Bell’s spaceship paradox, which is actually a consequence of Special relativity; I think that Boyes YouTube video is the easiest to follow.
Apart from ticking another item on my to-do list, I now appreciate some of the subtle points people make about General relativity. I’m sure that this knowledge will increase the likelihood of me getting in over my head in some future discussion on relativity.
Semantic pattern matching (Coccinelle)
I have just discovered Coccinelle a tool that claims to fill a remarkable narrow niche (providing semantic patch functionality; I have no idea how the name is pronounced) but appears to have a lot of other uses. The functionality required of a semantic patch is the ability to write source code patterns and a set of transformation rules that convert the input source into the desired output. What is so interesting about Coccinelle is its pattern matching ability and the ability to output what appears to be unpreprocessed source (it has to be told the usual compile time stuff about include directory paths and macros defined via the command line; it would be unfair of me to complain that it needs to build a symbol table).
Creating a pattern requires defining identifiers to have various properties (eg, an expression in the following example) followed by various snippets of code that specify the pattern to match (in the following <… …> represents a bracketed (in the C compound statement sense) don’t care sequence of code and the lines starting with +/- have the usual patch meaning (ie, add/delete line)). The tool builds an abstract syntax tree so urb is treated as a complete expression that needs to be mapped over to the added line).
@@ expression lock, flags; expression urb; @@ spin_lock_irqsave(lock, flags); <... - usb_submit_urb(urb) + usb_submit_urb(urb, GFP_ATOMIC) ...> spin_unlock_irqrestore(lock, flags); |
Coccinelle comes with a bunch of predefined equivalence relations (they are called isomophisms) so that constructs such as if (x), if (x != NULL) and if (NULL != x) are known to be equivalent, which reduces the combinatorial explosion that often occurs when writing patterns that can handle real-world code.
It is written in OCaml (I guess there had to be some fly in the ointment) and so presumably borrows a lot from CIL, perhaps in this case a version number of 0.1.3 is not as bad as it might sound.
My main interest is in counting occurrences of various kinds of patterns in source code. A short-term hack is to map the sought-for pattern to some unique character sequence and pipe the output through grep and wc. There does not seem to be any option to output a count of the matched patterns … yet 🙂
Recent Comments