Archive
Dimensional analysis of the Halstead metrics
One of the driving forces behind the Halstead complexity metrics was physics envy; the early reports by Halstead use the terms software physics and software science.
One very simple, and effective technique used by scientists and engineers to check whether an equation makes sense, is dimensional analysis. The basic idea is that when performing an operation between two variables, their measurement units must be consistent; for instance, two lengths can be added, but a length and a time cannot be added (a length can be divided by time, returning distance traveled per unit time, i.e., velocity).
Let’s run a dimensional analysis check on the Halstead equations.
The input variables to the Halstead metrics are: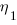 
, the number of distinct operators, 
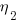, the number of distinct operands, 
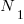, the total number of operators, and 
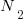, the total number of operands. These quantities can be interpreted as units of measurement in tokens.
The formula are:
- Program length:
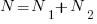
There is a consistent interpretation of this equation: operators and operands are both kinds of tokens, and number of tokens can be interpreted as a length. - Calculated program length:
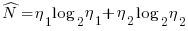
There is a consistent interpretation of this equation: the operand of a logarithm has to be dimensionless, and the convention is to treat the operand as a ratio (if no denominator is specified, the value 1 having the same dimensions as the numerator is taken, giving a dimensionless result), the value returned is dimensionless, which can be multiplied by a variable having any kind of dimension; so again two (token) lengths are being added. - Volume:
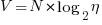
A volume has units of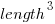
(i.e., it is created by multiplying three lengths). There is only one length in this equation; the equation is misnamed, it is a length. - Difficulty:
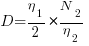
Here the dimensions of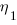 and 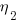cancel, leaving the dimensions of 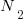(a length); now Halstead is interpreting length as a difficulty unit (whatever that might be). - Effort:
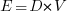
This equation multiplies two variables, both having a length dimension; the result should be interpreted as an area. In physics work is force times distance, and power is work per unit time; the term effort is not defined.
Halstead is claiming that a single dimension, program length, contains so much unique information that it can be used as a measure of a variety of disparate quantities.
Halstead’s colleagues at Purdue were rather damming in their analysis of these metrics. Their report Software Science Revisited: A Critical Analysis of the Theory and Its Empirical Support points out the lack of any theoretical foundation for some of the equations, that the analysis of the data was weak and that a more thorough analysis suggests theory and data don’t agree.
I pointed out in an earlier post, that people use Halstead’s metrics because everybody else does. This post is unlikely to change existing herd behavior, but it gives me another page to point people at, when people ask why I laugh at their use of these metrics.
Parsing Fortran 95
I have been looking at doing some dimensional analysis of the Climategate code and so needed a Fortran parser.
The last time I used Fortran in anger the modern compilers were claiming conformance to the 1977 standard and since then we have had Fortran 90 (with a minor revision in 95) and Fortran 03. I decided to take the opportunity to learn something about the new features by writing a Fortran parser that did not require a symbol table.
The Eli project had a Fortran 90 grammar that was close to having a form acceptable to bison and a few hours editing and debugging got me a grammar containing 6 shift/reduce conflicts and 1 reduce/reduce conflict. These conflicts looked like they could all be handled using glr parsing. The grammar contained 922 productions, somewhat large, but I was only interested in actively making use of parts of it.
For my lexer I planned to cut and paste an existing C/C++/Java lexer I have used for many projects. Now this sounds like a fundamental mistake, these languages treat whitespace as being significant while Fortran does not. This important difference is illustrated by the well known situation where a Fortran lexer needs to lookahead in the character stream to decide whether the next token is the keyword do or the identifier do5i (if 1 is followed by a comma it must be a keyword):
do 5 i = 1 , 10 do 5 i = 1 . 10 ! assign 1.10 to do5i 5 continue |
In my experience developers don’t break up literals or identifier names with whitespace, and so I planned to mostly ignore the whitespace issue (it would simplify things if some adjacent keywords were merged to create a single keyword).
In Fortran the I/O is specified in the language syntax, while in C like languages it is a runtime library call involving a string whose contents are interpreted at runtime. I decided to ignore I/O statements by skipping to the end of line (Fortran is line oriented).
Then the number of keywords hit me, around 190. Even with the simplifications, I had made writing a Fortran lexer look like it would be a lot of work; some of the keywords only had this status when followed by a = and I kept uncovering new issues. Cutting and pasting somebody else’s lexer would probably also involve a lot of work.
I went back and looked at some of the Fortran front ends I had found on the Internet. The GNU Fortran front-end was a huge beast and would need serious cutting back to be of use. moware was written in Fortran and used the traditional six character abbreviated names seen in ‘old-style’ Fortran source and not a lot of commenting. The Eli project seemed a lot more interested in the formalism side of things, and Fortran was just one of the languages they claimed to support.
The Open Fortran Parser looked very interesting. It was designed to be used as a parsing skeleton that could be used to produce tools that processed source, and already contained hooks that output diagnostic output when each language production was reduced during a parse. Tests showed that it did a good job of parsing the source I had, although there was one vendor extension used quite often (and not documented in their manual). The tool source, in Java, looked straightforward to follow, and it was obvious where my code needed to be added. This tool was exactly what I needed 🙂
Dimensional analysis of source code
The idea of restricting the operations that can be performed on a variable based on attributes appearing in its declaration is actually hundreds of years old and is more widely known as dimensional analysis. Readers are probably familiar with the concept of type checking where, for instance, a value having a floating-point type is not allowed to be added to a value having a pointer type. Unfortunately, many of those computer languages that support the functionality I am talking about (e.g., Ada) also refer to it as type checking and differentiate it from the more common usage by calling it strong typing. The concept would be much easier for people to understand if a different term were used, e.g., unit checking or even dimension checking.
Dimensional analysis, as used in engineering and the physical sciences, relies on the fact that quantities are often expressed in terms of a small number of basic attributes, e.g., mass, length and time; velocity is calculated by dividing a length by a time,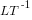 
and area is calculated by multiplying two lengths, 
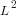. Adding a length quantity to a velocity has no physical meaning and suggests that something is wrong with the calculation, while dividing velocity by time, 
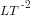, can be interpreted as acceleration. Dividing two quantities that have the same units results in what is known as a dimensionless number.
Dimensional analysis can be used to check a calculation involving physical quantities for internal consistency and as a method for trying to deduce the combinations of quantities that an unknown equation might contain based on the physical units the result is known to be represented in.
The frink language has units of measure checking built into it.
How might dimensional analysis be used to check source code for internal consistency? Consider the following code:
x = a / b; c = a; y = c / b; if (x + y ... ... z = x + b; |
c is assigned a‘s value and is therefore assumed to have the same units of measurement. The value assigned to y is calculated by dividing c by b and the train of reasoning leading to the assumption that it has the same units of measurement as x is easy to follow. Based on this analysis, there is nothing suspicious about adding x and y, but adding x and b looks wrong (it would be perfectly ok if all of the variables in this code were dimensionless).
A number of tools have been written to check source code expressions for internal consistency e.g., Fortran (Automated computation and consistency checking of physical dimensions and units in scientific programs), C++ (Applied Template Metaprogramming in SI units) and C (Annotation-less Unit Type Inference for C), but so far only one PhD.
Providing a mechanism for developers to add unit information to variable declarations would enable compilers to perform consistency checks and reduce the likelihood of false positives being reported (because dimensionless values can generally be combined in any way). It is too late in the day for such a major feature to be added to the next revision of the C++ standard; the C standard is also being revised, but the committee is currently being very conservative and insists that any proposed new constructs already be implemented in at least one compiler.
Recent Comments