Archive
if statement conditions, some basic measurements
The conditions contained in if-statements control all the decisions a program makes, yet relatively little is known about their characteristics.
A condition contains one or more clauses, for instance, the condition (a && b) contains two clauses that both need to be true, for the condition to be true. An earlier post modelled the number of clauses in Java conditions, and found an exponential decline (around 90% of conditions contained a single clause, for C this is around 85%).
The condition in a nested if-statement contains implicit decisions, because its evaluation depends on the conditions evaluated by its outer if-statements. I have long predicted that, on average, the number of clauses in a condition will decrease as if-statement nesting increases, because some decisions are subsumed by outer conditions. I have not seen any measurements on conditionals vs nesting, and this week this question reached the top of my to-do list.
I used Coccinelle to extract the text contained in each condition, along with the start/end line numbers of the associated if/else compound statement(s). After almost 20 years, Coccinelle is still the most flexible C source analysis tool available that does not require delving into compiler internals. The following is an example of the output (code and data):
file;stmt;if_line;if_col;cmpd_end;cmpd_line_end;expr sqlite-src-3460100/src/fkey.c;if;240;10;240;243;aiCol sqlite-src-3460100/src/fkey.c;if;217;6;217;217;! zKey sqlite-src-3460100/src/fkey.c;if;275;8;275;275;i == nCol sqlite-src-3460100/src/fkey.c;if;1428;6;1428;1433;aChange == 0 || fkParentIsModified ( pTab , pFKey , aChange , bChngRowid ) sqlite-src-3460100/src/fkey.c;if;808;4;808;808;iChildKey == pTab -> iPKey && bChngRowid sqlite-src-3460100/src/fkey.c;if;452;4;452;454;nIncr > 0 && pFKey -> isDeferred == 0 |
The conditional expressions (last column above) were reduced to a basic form involving simple variables and logical operators, along with operator counts. Some example output below (code and data):
simp_expr,land,lor,ternary v1,0,0,0 v1 && v2,1,0,0 v1 || v2,0,1,0 v1 && v2 && v3,2,0,0 v1 || ( v2 && v3 ),1,1,0 ( v1 && v2 ) || ( v3 && v4 ),2,1,0 ( v1 ? dm1 : dm2 ),0,0,1 |
The C source code projects measured were the latest stable versions of Vim (44,205 if-statements), SQLite (27,556 if-statements), and the Linux kernel (version 6.11.1; 1,446,872 if-statements).
A side note: I was surprised to see the ternary operator appearing in some conditions; in effect, an if within an if (see last line of the previous example). The ternary operator usually appears as a component of a large conditional expression (e.g., x + ( v1 ? dm1 : dm2 ) > y), rather than itself containing clauses, e.g., ( v1 ? dm1 : dm2 ) && v2. I have not seen the requirements for this operator discussed in any analysis of MC/DC.
The plot below shows the number of if-statements occurring at a given nesting level, along with regression fits, of the form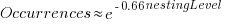 
, to the Vim and SQLite data; the Linux data was better fit by a power law (code+data):
I suspect that most of the deeply nested levels in Vim and SQLite are the results of long else if chains, which, while technically highly nested, could all have been written having the same nesting level, such as the following:
if (strcmp(x, "abc")) ; // code else if (strcmp(x, "xyz")) ; // code else if (strcmp(x, "123")) ; // code |
This if else pattern does not appear to be common in Linux. Perhaps ‘regularizing’ the if else sequences in Vim and SQLite will move the distribution towards a power law (i.e., like Linux).
Average nesting depth will also be affected by the average number of lines per function, with functions containing more statements providing the opportunity for more deeply nested if-statements (rather than calling a function containing nested if-statements).
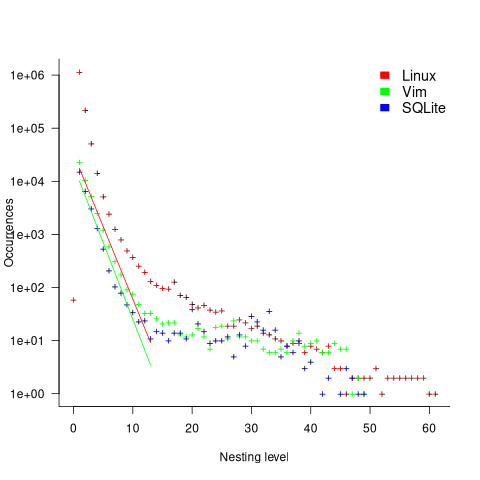
The plot below shows the number of occurrences of conditions containing a given number of clauses. Neither the exponential and power law are good fits, and log-log axis are used because it shows the points are closer to forming a straight line (code+data):
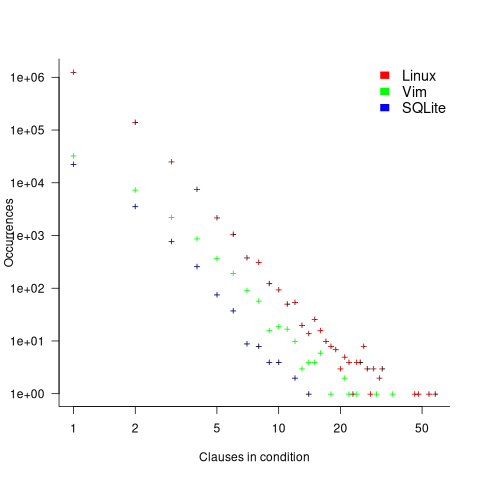
The plot below shows the nesting level and number of clauses in the condition for each of the 1,446,872 if-statements in the Linux kernel. Each value was ‘jittered’ to distribute points about their actual value, creating a more informative visualization (code+data):
As expected, the likelihood of a condition containing multiple clauses does decrease with nesting level. However, with around 85% of conditions containing a single clause, the fitted regression models essential predict one clause for all nesting levels.
Research ideas for 2023/2024
Students sometimes ask me for suggestions of interesting research problems in software engineering. A summary of my two recurring suggestions, for this year, appears below; 2016/2017 and 2019/2020 versions.
How many active users does a program or application have?
The greater the number of users, the greater the number of reported faults. Estimates of program reliability have to include volume of usage as an integral part of the calculation.
Non-trivial amounts of public data on program usage is non-existent (in a few commercial environments, users are charged for using software on a per-usage basis, but this data is confidential). Usage has to be estimated by indirect means.
A popular indirect technique for estimating the popularity of Github repos is to count the number of stars it has; however, stars have a variety of interpretations. The extent to which Github stars tracks usage of the repo’s software is not known.
Other indirect techniques include: web server logs, installs of the application, or the operating system.
One technique that has not yet been researched is to make use of the identity of those reporting faults. A parallel can be drawn with the fish population in lakes, which is not directly visible. Ecologists have developed techniques for indirectly estimating the population size of distinct creatures using information about a subset of the population, and some of the population models developed for ecology can be adapted to estimating program user populations.
Estimates of population size can be obtained by plugging information on the number of different people reporting faults, and the number of reports from the same person into these models. This approach is not as easy as it sounds because sometimes the same person has multiple identities, reported faults also need to be deduplicated and cleaned (30-40% of reports have been found to be requests for enhancements).
Nested if-statement execution
As if-statement nesting depth increases, the number of conditions controlling the execution of the enclosed code increases.
Being able to estimate the likelihood of executing the code controlled by an if-statement is of interest to: compilers wanting to target optimizations along the most frequently executed paths, special handling for error paths, testing along the least/most likely paths (e.g., fuzzers wanting to know the conditions needed to reach a given block), those wanting to organize code for ease of understanding, by reducing cognitive effort to understand.
Possible techniques for analysing the likelihood of executing code controlled by one or more nested if-statements include:
- Compiler writers have discovered various heuristics for predicting the likely outcome of a branch, and there are probably more to be discovered. Statement coverage counts provides a ground truth against which to compare ideas,
- analysis of the conditional expression,
- mathematical analysis of the distribution of values of variables in conditional expressions.
Some human biases in conditional reasoning
Tracking down coding mistakes is a common developer activity (for which training is rarely provided).
Debugging code involves reasoning about differences between the actual and expected output produced by particular program input. The goal is to figure out the coding mistake, or at least narrow down the portion of code likely to contain the mistake.
Interest in human reasoning dates back to at least ancient Greece, e.g., Aristotle and his syllogisms. The study of the psychology of reasoning is very recent; the field was essentially kick-started in 1966 by the surprising results of the Wason selection task.
Debugging involves a form of deductive reasoning known as conditional reasoning. The simplest form of conditional reasoning involves an input that can take one of two states, along with an output that can take one of two states. Using coding notation, this might be written as:
if (p) then q if (p) then !q if (!p) then q if (!p) then !q |
The notation used by the researchers who run these studies is a 2×2 contingency table (or conditional matrix):
OUTPUT
1 0
1 A B
INPUT
0 C D |
where: A, B, C, and D are the number of occurrences of each case; in code notation, p is the input and q the output.
The fertilizer-plant problem is an example of the kind of scenario subjects answer questions about in studies. Subjects are told that a horticultural laboratory is testing the effectiveness of 31 fertilizers on the flowering of plants; they are told the number of plants that flowered when given fertilizer (A), the number that did not flower when given fertilizer (B), the number that flowered when not given fertilizer (C), and the number that did not flower when not given any fertilizer (D). They are then asked to evaluate the effectiveness of the fertilizer on plant flowering. After the experiment, subjects are asked about any strategies they used to make judgments.
Needless to say, subjects do not make use of the available information in a way that researchers consider to be optimal, e.g., Allan’s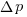 
index 
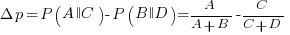(sorry about the double, 
, rather than single, vertical lines).
What do we know after 40+ years of active research into this basic form of conditional reasoning?
The results consistently find, for this and other problems, that the information A is given more weight than B, which is given by weight than C, which is given more weight than D.
That information provided by A and B is given more weight than C and D is an example of a positive test strategy, a well-known human characteristic.
Various models have been proposed to ‘explain’ the relative ordering of information weighting: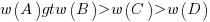 
, e.g., that subjects have a bias towards sufficiency information compared to necessary information.
Subjects do not always analyse separate contingency tables in isolation. The term blocking is given to the situation where the predictive strength of one input is influenced by the predictive strength of another input (this process is sometimes known as the cue competition effect). Debugging is an evolutionary process, often involving multiple test inputs. I’m sure readers will be familiar with the situation where the output behavior from one input motivates a misinterpretation of the behaviour produced by a different input.
The use of logical inference is a commonly used approach to the debugging process (my suggestions that a statistical approach may at times be more effective tend to attract odd looks). Early studies of contingency reasoning were dominated by statistical models, with inferential models appearing later.
Debugging also involves causal reasoning, i.e., searching for the coding mistake that is causing the current output to be different from that expected. False beliefs about causal relationships can be a huge waste of developer time, and research on the illusion of causality investigates, among other things, how human interpretation of the information contained in contingency tables can be ‘de-biased’.
The apparently simple problem of human conditional reasoning over two variables, each having two states, has proven to be a surprisingly difficult to model. It is tempting to think that the performance of professional software developers would be closer to the ideal, compared to the typical experimental subject (e.g., psychology undergraduates or Mturk workers), but I’m not sure whether I would put money on it.
How should involved if-statement conditionals be structured?
Which of the following two if-statements do you think will be processed by readers in less time, and with fewer errors, when given the value of x, and asked to specify the output?
// First - sequence of subexpressions if (x > 0 && x < 10 || x > 20 && x < 30) print("a"); else print "b"); // Second - nested ifs if (x > 0 && x < 10) print("c"); else if (x > 20 && x < 30) print("d"); else print("e"); |
Ok, the behavior is not identical, in that the else if-arm produces different output than the preceding if-arm.
The paper Syntax, Predicates, Idioms — What Really Affects Code Complexity? analyses the results of an experiment that asked this question, including more deeply nested if-statements, the use of negation, and some for-statement questions (this post only considers the number of conditions/depth of nesting components). A total of 1,583 questions were answered by 220 professional developers, with 415 incorrect answers.
Based on the coefficients of regression models fitted to the results, subjects processed the nested form both faster and with fewer incorrect answers (code+data). As expected performance got slower, and more incorrect answers given, as the number of intervals in the if-condition increased (up to four in this experiment).
I think short-term memory is involved in this difference in performance; or at least I can concoct a theory that involves a capacity limited memory. Comprehending an expression (such as the conditional in an if-statement) requires maintaining information about the various components of the expression in working memory. When the first subexpression of x > 0 && x < 10 || x > 20 && x < 30 is false, and the subexpression after the || is processed, there is no now forget-what-went-before point like there is for the nested if-statements. I think that the single expression form is consuming more working memory than the nested form.
Does the result of this experiment (assuming it is replicated) mean that developers should be recommended to write sequences of conditions (e.g., the first if-statement example) about as:
if (x > 0 && x < 10) print("a"); else if (x > 20 && x < 30) print("a"); else print("b"); |
Duplicating code is not good, because both arms have to be kept in sync; ok, a function could be created, but this is extra effort. As other factors are taken into account, the costs of the nested form start to build up, is the benefit really worth the cost?
Answering this question is likely to need a lot of work, and it would be a more efficient use of resources to address questions about more commonly occurring conditions first.
A commonly occurring use is testing a single range; some of the ways of writing the range test include:
if (x > 0 && x < 10) ... if (0 < x && x < 10) ... if (10 > x && x > 0) ... if (x > 0 && 10 > x) ... |
Does one way of testing the range require less effort for readers to comprehend, and be more likely to be interpreted correctly?
There have been some experiments showing that people are more likely to give correct answers to questions involving information expressed as linear syllogisms, if the extremes are at the start/end of the sequence, such as in the following:
A is better than B
B is better than C |
and not the following (which got the lowest percentage of correct answers):
B is better than C
B is worse than A |
Your author ran an experiment to find out whether developers were more likely to give correct answers for particular forms of range tests in if-conditions.
Out of a total of 844 answers, 40 were answered incorrectly (roughly one per subject; it was a paper and pencil experiment, so no timings). It's good to see that the subjects were so competent, but with so few mistakes made the error bars are very wide, i.e., too few mistakes were made to be able to say that one representation was less mistake-prone than another.
I hope this post has got other researchers interested in understanding developer performance, when processing if-statements, and that they will be running more experiments help shed light on the processes involved.
Calculating statement execution likelihood
In the following code, how often will the variable b be incremented, compared to a?
If we assume that the variables x and y have values drawn from the same distribution, then the condition (x < y) will be true 50% of the time (ignoring the situation where both values are equal), i.e., b will be incremented half as often as a.
a++; if (x < y) { b++; if (x < z) { c++; } } |
If the value of z is drawn from the same distribution as x and y, how often will c be incremented compared to a?
The test (x < y) reduces the possible values that x can take, which means that in the comparison (x < z), the value of x is no longer drawn from the same distribution as z.
Since we are assuming that z and y are drawn from the same distribution, there is a 50% chance that (z < y).
If we assume that (z < y), then the values of x and z are drawn from the same distribution, and in this case there is a 50% change that (x < z) is true.
Combining these two cases, we deduce that, given the statement a++; is executed, there is a 25% probability that the statement c++; is executed.
If the condition (x < z) is replaced by (x > z), the expected probability remains unchanged.
If the values of x, y, and z are not drawn from the same distribution, things get complicated.
Let's assume that the probability of particular values of x and y occurring are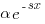 
and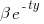 
, respectively. The constants 
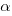and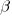 
are needed to ensure that both probabilities sum to one; the exponents 
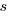and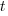 
control the distribution of values. What is the probability that (x < y) is true?
Probability theory tells us that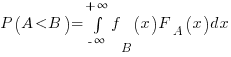 
, where: 
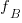is the probability distribution function for 
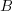(in this case: 
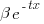), and 
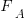the cumulative probability distribution for 
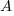(in this case: 
).
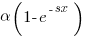Doing the maths gives the probability of (x < y) being true as: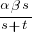 
.
The (x < z) case can be similarly derived, and combining everything is just a matter of getting the algebra right; it is left as an exercise to the reader :-)
Growth of conditional complexity with file size
Conditional statements are a fundamental constituent of programs. Conditions are driven by the requirements of the problem being solved, e.g., if the water level is below the minimum, then add more water. As the problem being solved gets more complicated, dependencies between subproblems grow, requiring an increasing number of situations to be checked.
A condition contains one or more clauses, e.g., a single clause in: if (a==1), and two clauses in: if ((x==y) && (z==3)); a condition also appears as the termination test in a for-loop.
How many conditions containing one clause will a 10,000 line program contain? What will be the distribution of the number of clauses in conditions?
A while back I read a paper studying this problem (“What to expect of predicates: An empirical analysis of predicates in real world programs”; Google currently not finding a copy online, grrr, you will have to hassle the first author: durelli@icmc.usp.br, or perhaps it will get added to a list of favorite publications {be nice, they did publish some very interesting data}) it contained a table of numbers and yesterday my analysis of the data revealed a surprising pattern.
The data consists of SLOC, number of files and number of conditions containing a given number of clauses, for 63 Java programs. The following plot shows percentage of conditionals containing a given number of clauses (code+data):
The fitted equation, for the number of conditionals containing a given number of clauses, is:
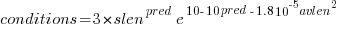
where: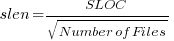 
(the coefficient for the fitted regression model is 0.56, but square-root is easier to remember), 
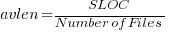, and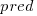 
is the number of clauses.
The fitted regression model is not as good when 
or 
is always used.
This equation is an emergent property of the code; simply merging files to increase the average length will not change the distribution of clauses in conditionals.
When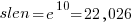 
, all conditionals contain the same number of clauses, off to infinity. For the 63 Java programs, the mean was 2,625, maximum 11,710, and minimum 172.
I was expecting SLOC to have an impact, but was not expecting number of files to be involved.
What grows with SLOC? Number of global variables and number of dependencies. There are more things available to be checked in larger programs, and an increase in dependencies creates the need to perform more checks. Also, larger programs are likely to contain more special cases, which are likely to involve checking both general and specific values (i.e., more clauses in conditionals); ok, this second sentence is a bit more arm-wavy than the first. The prediction here is that the percentage of global variables appearing in conditions increases with SLOC.
Chopping stuff up into separate files has a moderating effect. Since I did not expect this, I don’t have much else to say.
This model explains 74% of the variance in the data (impressive, if I say so myself). What other factors might be involved? Depth of nesting would be my top candidate.
Removing non-if-statement related conditionals from the count would help clarify things (I don’t expect loop-controlling conditions to be related to amount of code).
Two interesting data-sets in one week, with 10-days still to go until Christmas 🙂
Update: Fitting the same equation to the data from a later paper by the same group, based on mobile applications written in Swift and Objective-C, also produces a well-fitted regression model (apart from the term specifying an interactions between and 
).
Update: Thanks to Frank Busse for reminding me of the FAA report An Investigation of Three Forms of the Modified Condition Decision Coverage (MCDC) Criterion, which contains detailed information on the 20,256 conditionals in five Ada programs. The number of conditionals containing a given number of clauses is fitted by a power law (exponent is approximately -3).
Fingerprinting the author of the ZeuS Botnet
The source code of the ZeuS Botnet is now available for download. I imagine there are a few organizations who would like to talk to the author(s) of this code.
All developers have coding habits, that is they usually have a particular way of writing each coding construct. Different developers have different sets of habits and sometimes individual developers have a way of writing some language construct that is rarely used by other developers. Are developer habits sufficiently unique that they can be used to identify individuals from their code? I don’t have enough data to answer that question. Reading through the C++ source of ZeuS I spotted a few unusual usage patterns (I don’t know enough about common usage patterns in PHP to say much about this source) which readers might like to look for in code they encounter, perhaps putting name to the author of this code.
The source is written in C++ (32.5 KLOC of client source) and PHP (7.5KLOC of server source) and is of high quality (the C++ code could do with more comments, say to the level given in the PHP code), many companies could increase the quality of their code by following the coding standard that this author seems to be following. The source is well laid out and there are plenty of meaningful variable names.
So what can we tell about the person(s) who wrote this code?
- There is one author; this is based on consistent usage patterns and nothing jumping out at me as being sufficiently different that it could be written by somebody else,
- The author is fluent in English; based on the fact that I did not spot any identifiers spelled using unusual word combinations that often occur when a developer has a poor grasp of English. Update 16-May: skier.su spotted four instances of the debug message “Request sended.” which suggests the author is not as fluent as I first thought.
- The usage that jumped out at me the most is:
for(;; p++)if(*p == '\\' || *p == '/' || *p == 0) { ...
This is taking to an extreme the idea that if a ‘control header’ has a single statement associated with it, then they both appear on the same line; this usage commonly occurs with if-statements and this for/while-statement usage is very rare (this usage also occurs in the PHP code),
- The usage of
true/falsein conditionals is similar to that of newbie developers, for instance writing:return CWA(kernel32, RemoveDirectoryW)(path) == FALSE ? false : true; // and return CWA(shlwapi, PathCombineW)(dest, dir, p) == NULL ? false : true; // also return CWA(kernel32, DeleteFileW)(file) ? true : false;
in a function returning
boolinstead of:return CWA(kernel32, RemoveDirectoryW)(path); //and return CWA(shlwapi, PathCombineW)(dest, dir, p) != NULL // and return CWA(kernel32, DeleteFileW)(file);
The author is not a newbie developer, perhaps sometime in the past they were badly bitten by a Microsoft C++ compiler bug, found that this usage worked around the problem and have used it ever since,
- The author vertically aligns the assignment operator in statement sequences but not in a sequence of definitions containing an initializer:
// = not vertically aligned here DWORD itemMask = curItem->flags & ITEMF_IS_MASK; ITEM *cloneOfItem = curItem; // but is vertically aligned here: desiredAccess |= GENERIC_WRITE; creationDisposition = OPEN_ALWAYS;
Vertical alignment is not common and I would have said that alignment was more often seen in definitions than statements, the reverse of what is seen in this code,
- Non-terminating loops are created using
for(;;)rather than the more commonly seenwhile(TRUE), - The author is happy to use
gototo jump to the end of a function, not a rare habit but lots of developers have been taught that such usage is bad practice (I would say it depends, but that discussion belongs in another post), - Unnecessary casts often appear on negative constants (unnecessary in the sense that the compiler is required to implicitly do the conversion). This could be another instance of a previous Microsoft compiler bug causing a developer to adopt a coding habit to work around the problem.
Could the source have been processed by an code formatter to remove fingerprint information? I think not. There are small inconsistencies in layout here and there that suggest human error, also automatic layout tends to have a ‘template’ look to it that this code does not have.
Update 16 May: One source file stands out as being the only one that does not make extensive use of camelCase and a quick search finds that it is derived from the ucl compression library.
Recent Comments