Archive
Estimating variance when measuring source
Yesterday I finally delivered a paper on if/switch usage measurements to the ACCU magazine editor and today I read about a switch statement usage that, if common, would invalidate a chunk of my results. Does anything jump out at you in the following snippet?
switch (x) { case 1: { z++; ... break; } ... |
switch (x) { case 1: { z++; ... break; } ...
Yes, those { } delimiting the case-labeled statement sequence. A quick check of my C source benchmarks showed this usage occurring in around 1% of case-labels. Panic over.
What is the statistical significance, i.e., variance, of that 1%? Have I simply measured an unrepresentative sample, what would be a representative sample and what would be the expected variance within a representative sample?
I am interested in commercial software development, and so I have selected half a dozen or so largish code bases as my source benchmark, preferably written in a commercial environment even if currently available as Open source. I would prefer this benchmark to be an order of magnitude larger, and perhaps I will get around to adding more programs soon.
My if/switch measurements were aimed at finding usage characteristics that varied between the two kinds of selection statements. One characteristic measured was the number of equality tests in the associated controlling expression. For instance, in:
if (x == 1 || x == 2) z--; else if (x == 3) z++; |
if (x == 1 || x == 2) z--; else if (x == 3) z++;
the first controlling expression contains two equality tests, and the second one equality test.
Plotting the percentage of equality tests that occur in the controlling expressions of if-if/if-else-if sequences and switch statements, we get the following:
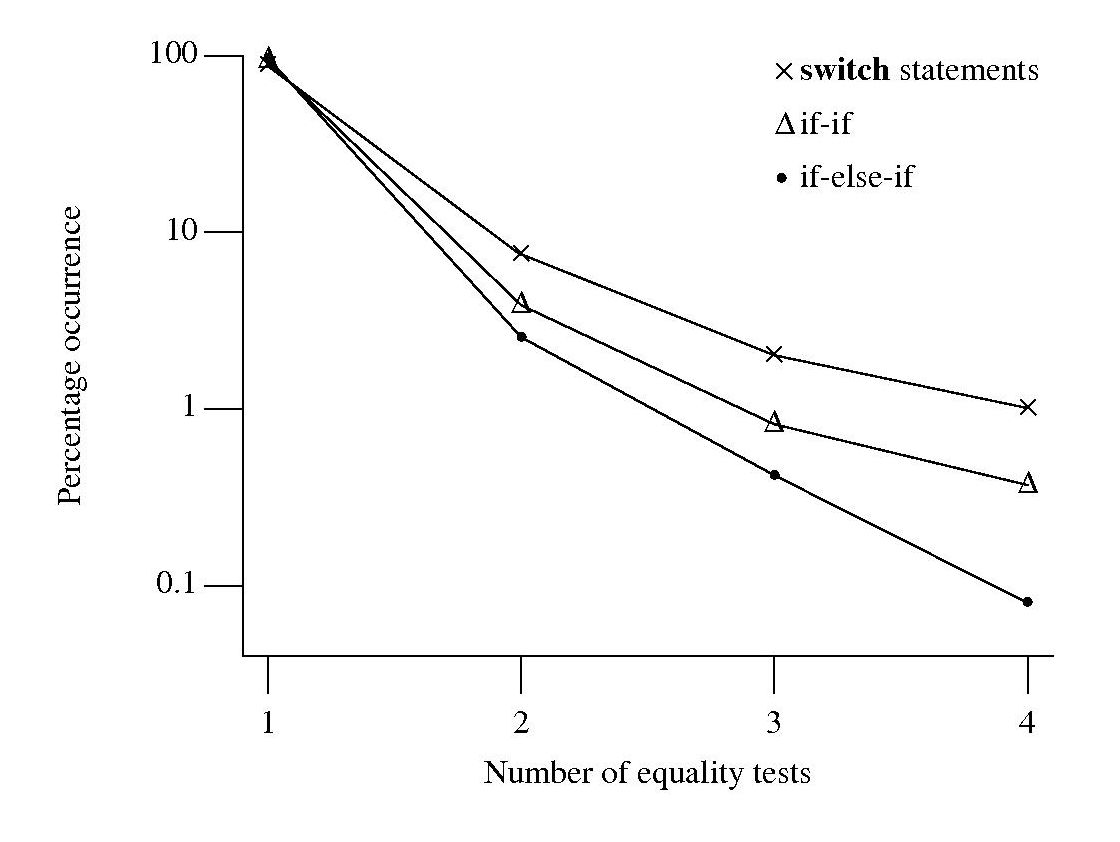
Do these results indicate that if-if/if-else-if sequences and switch statements differ in the number of equality tests contained in their controlling expressions? If I measured a completely different set of source code, would the results be very different?
To answer this question, a probability model is needed. Take as an example, the controlling expressions present in an if-if sequence. If each controlling expression is independent of the others, then the probability of two equality tests, for instance, occurring in any of these expressions is constant and thus given a large sample the distribution of two equality tests in the source has a binomial distribution. The same argument can be applied to other numbers of equality tests and other kinds of sequence.

For each measurement point in the above plot the associated error bars span the square-root of the variance of that point (assuming a binomial distribution, for a normal distribution the length of this span is known as the standard deviation). The error bars overlap, suggesting that the apparent difference in percentage of equality tests in each kind of sequence is not statistically significant.
The existence of some dependency between controlling expression equality tests would invalidate this simply analysis, or at least reduce its reliability. I did notice that in a sequence that containing two equality tests, the controlling expression that contained it tended to appear later in the sequence (the reverse of the example given above). Did I notice this because I tend to write this way? A question for another day.
Recent Posts
Tags
Archives
- June 2025
- May 2025
- April 2025
- March 2025
- February 2025
- January 2025
- December 2024
- November 2024
- October 2024
- September 2024
- August 2024
- July 2024
- June 2024
- May 2024
- April 2024
- March 2024
- February 2024
- January 2024
- December 2023
- November 2023
- October 2023
- September 2023
- August 2023
- July 2023
- June 2023
- May 2023
- April 2023
- March 2023
- February 2023
- January 2023
- December 2022
- November 2022
- October 2022
- September 2022
- August 2022
- July 2022
- June 2022
- May 2022
- April 2022
- March 2022
- February 2022
- January 2022
- December 2021
- November 2021
- October 2021
- September 2021
- August 2021
- July 2021
- June 2021
- May 2021
- April 2021
- March 2021
- February 2021
- January 2021
- December 2020
- November 2020
- October 2020
- September 2020
- August 2020
- July 2020
- June 2020
- May 2020
- April 2020
- March 2020
- February 2020
- January 2020
- December 2019
- November 2019
- October 2019
- September 2019
- August 2019
- July 2019
- June 2019
- May 2019
- April 2019
- March 2019
- February 2019
- January 2019
- December 2018
- November 2018
- October 2018
- September 2018
- August 2018
- July 2018
- June 2018
- May 2018
- April 2018
- March 2018
- February 2018
- January 2018
- December 2017
- November 2017
- October 2017
- September 2017
- August 2017
- July 2017
- June 2017
- May 2017
- April 2017
- March 2017
- February 2017
- January 2017
- December 2016
- November 2016
- October 2016
- September 2016
- August 2016
- July 2016
- June 2016
- May 2016
- April 2016
- March 2016
- February 2016
- January 2016
- December 2015
- November 2015
- October 2015
- September 2015
- August 2015
- July 2015
- June 2015
- May 2015
- April 2015
- March 2015
- February 2015
- January 2015
- December 2014
- November 2014
- October 2014
- September 2014
- August 2014
- July 2014
- June 2014
- May 2014
- April 2014
- March 2014
- February 2014
- January 2014
- December 2013
- November 2013
- October 2013
- September 2013
- August 2013
- July 2013
- June 2013
- May 2013
- April 2013
- March 2013
- February 2013
- January 2013
- December 2012
- November 2012
- October 2012
- September 2012
- August 2012
- July 2012
- June 2012
- May 2012
- April 2012
- March 2012
- February 2012
- January 2012
- December 2011
- November 2011
- October 2011
- September 2011
- August 2011
- July 2011
- June 2011
- May 2011
- April 2011
- March 2011
- February 2011
- January 2011
- December 2010
- November 2010
- October 2010
- September 2010
- August 2010
- July 2010
- June 2010
- May 2010
- April 2010
- March 2010
- February 2010
- January 2010
- December 2009
- November 2009
- October 2009
- September 2009
- August 2009
- July 2009
- June 2009
- May 2009
- April 2009
- March 2009
- February 2009
- January 2009
- December 2008
Recent Comments