Archive
Hexadecimal usage in Google’s scanned books
After investigating programming language name usage in Google’s ngram viewer, I decided to try something more specific. Hexadecimal literals are an interesting subproblem in optical character recognition; a little uncertainty in an image can result in a character sequence being equally viable as a word or a hexadecimal literal.
I downloaded all the Google books 1-grams and started to experiment. I eventually considered any character sequence matching the pattern ^[0oO][xX][0-9a-fA-FoOl] for further analysis; that is ohh, Ohh and ell were treated as the corresponding digits.
This prefix matching reduced 473 million possibilities down to 89 thousand.
Next any character sequence containing a non-hex character (again ohh, Ohh and ell were treated as special cases) was removed, bringing the possibilities down to 20 thousand.
When did the first hexadecimal literal appear in print? I settled on a generous view of history, 1945; also the sequence oxo seemed surprisingly common and looking at a few of the contexts in which it occurred I decided that most of the usage related to chemical formula and removed all matches. The post-1945 and oxo checks removed a third of remaining character sequences.
It seems to me that if any hexadecimal literal appears in a book, at least one more is likely to occur. Google does not provide a breakdown of each character sequence by book; for a given character sequence, the total count for each year is given, along with the number of pages it occurred on in that year and the number of different books it appeared within in the year. If the number of occurrences of a character sequence in a given year equalled the number of different books I excluded the usage count; this reduced the number of matches from 13,729 to 7,292; with 319 unique character sequences.
Are the remaining of character sequences a reasonably accurate list of hexadecimal literals appearing in the books that Google has scanned? Is 0.15 hexadecimal literals per million words a reasonable value?
A while back, I did some analysis of C source usage that included checking whether integer literals followed Benford’s law. Extracting the first non-zero digit from the character sequences extracted from Google books and comparing them with the C source hexadecimal data we get:
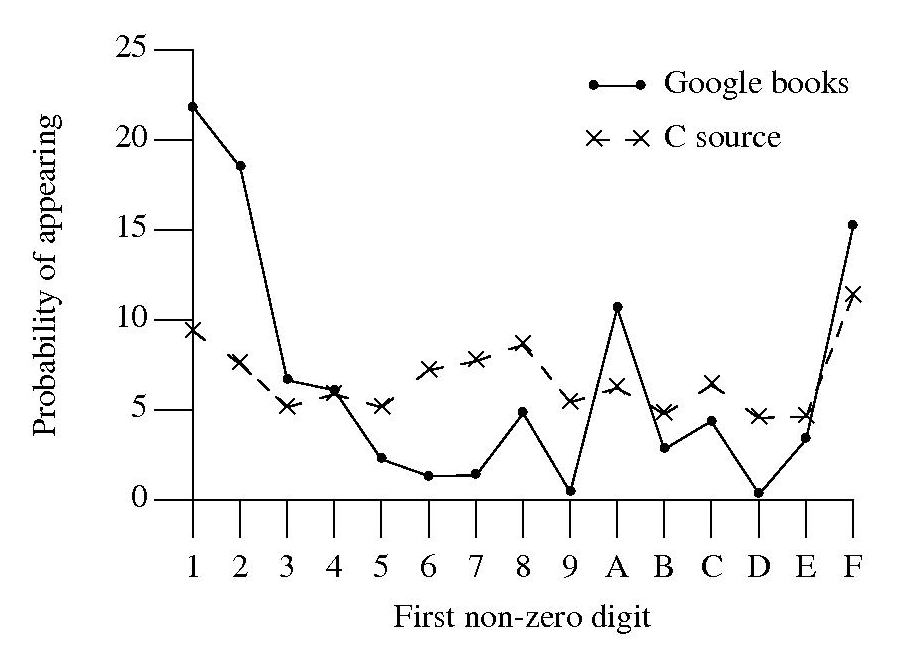
Both plots share ‘spikes’ at five values, but the pattern of relative sizes is different. Perhaps the pattern of hexadecimal literal usage in C source is slightly different from what occurs in other languages, or perhaps the relatively large percentage of 1 occurs because ell is accepted.
The context in which a character sequenced occurred would probably be a very good indicator of whether it was a hexadecimal literal or not. Google only provide a subset of their 2-grams and any analysis of these will have to wait for another time; however I did quickly check to see whether the OCR process had resulted in a single literal being split into two separate sequences, a manual check of the 95 possible sequences I found showed that most were not good candidates for a split literal.
The final list of ‘hexadecimal literal’s and their occurrence counts is available for download.
Benford’s law and numeric literals in source code
Benford’s law applies to values derived from a surprising number of natural and man-made processes. I was very optimistic that it would also apply to numeric literals in source code. Measurements of C source showed that I was wrong (the chi-square fit was 1,680 for decimal integer literals and 132,398 for floating literals).
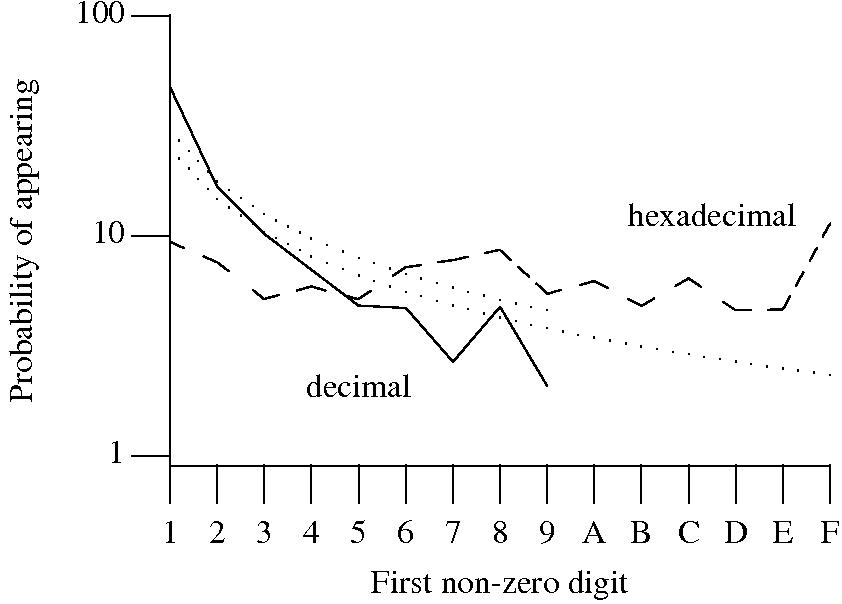
Probability that the leading digit of an (decimal or hexadecimal) integer literal has a particular value (dotted lines predicted by Benford’s law).
What are the conditions necessary for a sample of values to follow Benford’s law? A number of circumstances have been found to result in sample values having a leading digit that follows Benford’s law, including:
Samples that have been found to follow Benford’s law include lists of physical constants and accounting data (so much so that it has been used to detect accounting fraud). However, the number of data-sets containing values whose leading digit follows Benford’s law is not a great as some would make us believe.
Why don’t the leading digits of numeric literals in source code follow Benford’s law?
++/-- operators reduces the number of instances of 1 to increment/decrement a value). But this only applies to integer types, not floating types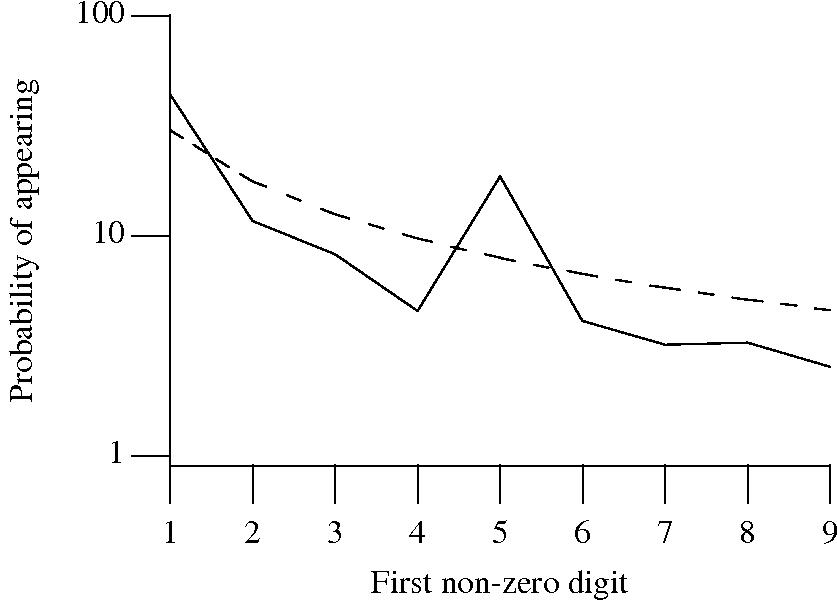
Probability that the leading, first non-zero, digit of a floating literal has a particular value (dashed line predicted by Benford’s law).
5 for the floating-point literals? Have values been rounded to produce 0.5? This looks like an area where methods used for accounting fraud detection might be applied (not that any fraud is implied, just irregularity).These surprising measurements show that there is a lot to the shape of numeric literals that is yet to be discovered.
Recent Comments