Archive
Ability to remember code improves with experience
What mental abilities separate an expert from a beginner?
In the 1940s de Groot studied expertise in Chess. Players were shown a chess board containing various pieces and then asked to recall the locations of the pieces. When the location of the chess pieces was consistent with a likely game, experts significantly outperformed beginners in correct recall of piece location, but when the pieces were placed at random there was little difference in recall performance between experts and beginners. Also players having the rank of Master were able to reconstruct the positions almost perfectly after viewing the board for just 5 seconds; a recall performance that dropped off sharply with chess ranking.
The interpretation of these results (which have been duplicated in other areas) is that experts have learned how to process and organize information (in their field) as chunks, allowing them to meaningfully structure and interpret board positions; beginners don’t have this ability to organize information and are forced to remember individual pieces.
In 1981 McKeithen, Reitman, Rueter and Hirtle repeated this experiment, but this time using 31 lines of code and programmers of various skill levels. Subjects were given two minutes to study 31 lines of code, followed by three minutes to write (on a blank sheet of paper) all the code they could recall; this process was repeated five times (for the same code). The plot below shows the number of lines correctly recalled by experts (2,000+ hours programming experience), intermediates (just finished programming course) and beginners (just started programming course), left performance using ‘normal’ code and right is performance viewing code created by randomizing lines from ‘normal’ code; only the mean values in each category are available (code+data):
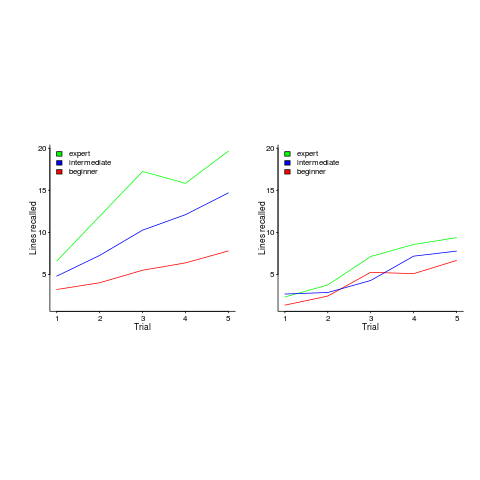
Experts start off remembering more than beginners and their performance improves faster with practice.
Compared to the Power law of practice (where experts should not get a lot better, but beginners should improve a lot), this technique is a much less time consuming way of telling if somebody is an expert or beginner; it also has the advantage of not requiring any application domain knowledge.
If you have 30 minutes to spare, why not test your ‘expertise’ on this code (the .c file, not the .R file that plotted the figure above). It’s 40 odd lines of C from the Linux kernel. I picked C because people who know C++, Java, PHP, etc should have no trouble using existing skills to remember it. What to do:
- You need five blank sheets of paper, a pen, a timer and a way of viewing/not viewing the code,
- view the code for 2 minutes,
- spend 3 minutes writing down what you remember on a clean sheet of paper,
- repeat until done 5 times.
Count how many lines you correctly wrote down for each iteration (let’s not get too fussed about exact indentation when comparing) and send these counts to me (derek at the primary domain used for this blog), plus some basic information on your experience (say years coding in language X, years in Y). It’s anonymous, so don’t include any identifying information.
I will wait a few weeks and then write up the data o this blog, as well as sharing the data.
Update: The first bug in the experiment has been reported. It takes longer than 3 minutes to write out all the code. Options are to stick with the 3 minutes or to spend more time writing. I will leave the choice up to you. In a test situation, maximum time is likely to be fixed, but if you have the time and want to find out how much you remember, go for it.
Power law of practice in software implementation
People get better with practice. The power law of practice specifies 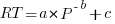 , where:
, where:  is the response time,
is the response time,  the amount of practice and
the amount of practice and  ,
,  and
and  are constants. However, sometimes an exponential equation is a better fit for to the data:
are constants. However, sometimes an exponential equation is a better fit for to the data: 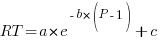 . There are theoretical reasons for liking a power law (e.g., it can be derived from the chunking of information), but it is difficult to argue with the exponential fitting so much data better than a power law.
. There are theoretical reasons for liking a power law (e.g., it can be derived from the chunking of information), but it is difficult to argue with the exponential fitting so much data better than a power law.
The plot below, from a study by Alteneder, shows the time taken to solve the same jig-saw puzzle, for 35 trials (red); followed by a two week pause and another 35 trials (in blue; if anybody else wants to try this, a dedicated weekend should be long enough to complete over 20 trials). The lines are fitted power law and exponential equations (code+data). Can you tell which is which?
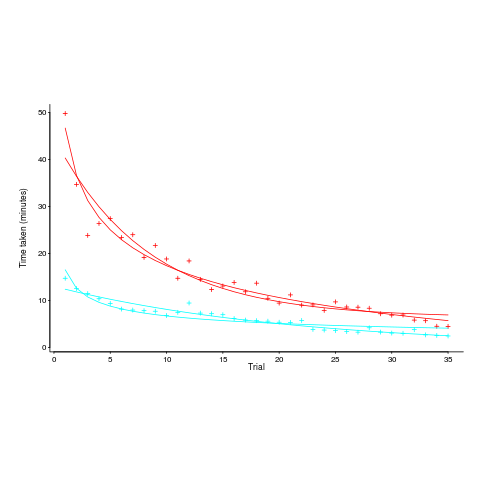
To find out if the same behavior occurs with software we need data on developers implementing the identical applications multiple times. I know of two experiments where the same application has been implemented multiple times by the same people, and where the data is available. Please let me know if you know of any others.
Zislis timed himself implementing 12 algorithms from the CACM collection in each of three languages, iterating four times (my copy came from the Purdue library, which as I write this is not listing the report). The large number of different programs implemented, coupled with the use of multiple languages, makes it difficult to separate out learning effects.
Lui and Chan ran an experiment where 24 developers (8 pairs {pair programming} and 8 singles) implemented the same application four times. The plot below shows the time taken to complete each implementation (singles top, pairs bottom, with black cross showing predictions made by a power law fit).
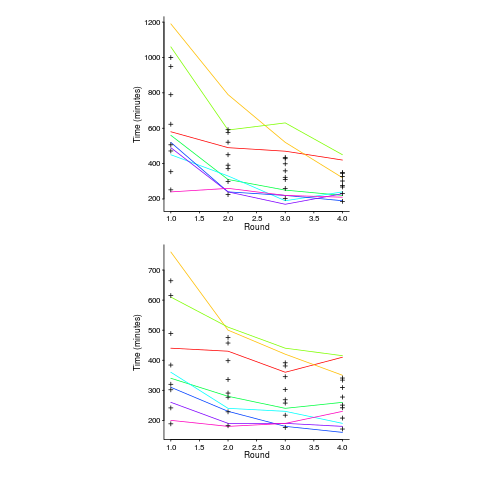
Different subjects start the experiment with different amounts of ability and past experience. Before starting, subjects took a multiple choice test of their knowledge. If we take the results of this test as a proxy for the ability/knowledge at the start of the experiment, then the power law equation becomes (a similar modification can be made to the exponential equation):
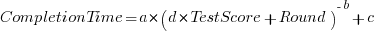
That is, the test score is treated as equivalent to performing some number of rounds of implementation). A power law is a better fit than exponential to this data (code+data); the fit captures the general shape, but misses lots of what look like important details.
The experiment was run over successive weekends. So there was opportunity for some forgetting to occur during the week days, and the amount forgotten will vary between people. It is easy to think of other issues that could have influenced subject performance.
This experiment must rank as one of the most interesting software engineering experiments performed to date.
Recent Comments