Archive
Techniques used for analyzing basic performance measurements
The statistical design and analysis of experiments is a relatively recent invention (around 150 years old; verifying scientific hypotheses using experiments was first proposed over 1,000 years ago).
Once an experiment has been run, and performance measurements collected, what techniques are available to analyse the data?
Before electronic computers were invented, the practical statistical techniques were those that could be performed manually (perhaps with some help from a mechanical calculator).
Once computers became available, these manual use techniques were widely implemented in statistical applications and libraries. New statistical techniques have been invented that are only of practical when a computer is available, e.g., the bootstrap.
Most researchers in software engineering remain stuck in the pre-computer world of statistical analysis, i.e., failing to use more powerful techniques that make use of computers. Software engineering is not unique in being stuck using pre-computer statistical techniques, there are many other fields that have failed to move on to the more flexible and powerful techniques now available.
Performance comparison by benchmarking (i.e., running an experiment) is a common activity in scientific and engineering fields. Once the measurements have been made, what is the difference between pre-computer and post-manual statistical comparison techniques?
Performance comparison invariably involves comparing the mean/average of each set of measurements (one set for each product benchmarked). Random variations will have some impact on the measured values, and it’s possible that any difference in mean values is the result of these random variations. There are statistical tests for estimating the likelihood of the difference being due to random variation.
Statistical tests invariably come with preconditions on the characteristics of their input data, i.e., the test only works as advertised if the preconditions are met.
The t.test is a popular pre-computer method of estimating the likelihood that the difference between the means of two sets of measurements occurred by chance. Two of its preconditions are that the two sets of input data have a Normal/Gaussian distribution, and have the same standard deviation (if the standard deviations are not equal, Welch’s t-test should be used).
The Mann–Whitney U test (also known as the Wilcoxon rank-sum test) is a pre-computer method with a more relaxed precondition on the distribution of the inputs, requiring only that they are drawn from the same distribution (which need not be a Normal distribution; it is a non-parametric test). This test returns the likelihood of one group being less/greater than the other, and says nothing about the magnitude of the difference.
Removing the constraint that it must be practical to manually perform the calculations, led, in 1979, to a paper proposing the Bootstrap (major issues around the theory underpinning the bootstrap were answered by the early 1990s).
The Bootstrap, a post-manual method, does not have any preconditions on the distribution or standard deviation of the input data. An important precondition is that it is reasonable to assume that the elements of the two sets of measurements are exchangeable (more on this below).
The Bootstrap is a general technique that is not limited to only comparing mean values, it can be used to compare any quantity of interest (assuming the appropriate data is available).
The bootstrap algorithm starts by assuming that, if the two samples are combined into an aggregate sample, all possible permutations of values in this aggregate into two samples are equally likely (this is the exchangeability assumption). If this assumption is true, then any compared difference in the measured two samples will be roughly the same as the compared difference in a pair of random samples drawn from the aggregate.
The computational intensive component of a bootstrap test is generating many pairs of random samples (5,000 is a common choice; sampling with replacement, and saving the result of the comparison).
The comparison results of the paired random samples and the two measured samples are sorted. The position of the measured comparison in this sorted list is the test statistic, i.e., how extreme is the result from the measured samples, compared to the random samples?
News of the flexibility and power of the bootstrap are slowly permeating through the research community. There is an existing way of doing things, and there is little incentive to change. As Plank famously observed: “Science advances one funeral at a time.”
Learning General relativity at a rudimentary mathematical level
For the longest time, I have wanted to have an understanding of Einstein’s theory of General relativity at a rudimentary mathematical level. Because General relativity has never been a mainstream topic in undergraduate physics, there are almost no books at this level. Also, the mathematics of General relativity is based on tensor calculus, which until recently was rarely used in engineering and non-relativistic physics; market size explains the lack of non-specialist books on the subject.
The Theoretical Minimum is a book series that aims to teach everything required to gain a basic understanding of various areas of modern physics. The primary author of the books is Leonard Susskind.
At the start of this year, “General Relativity: The Theoretical Minimum” by Susskind and Cabannes was published as a paperback (i.e., convenient for reading on the London Underground), and over the last two months I have been slowly working my way through it.
At the start of this week, I discovered Eddie Boyes’ YouTube series on General relativity.
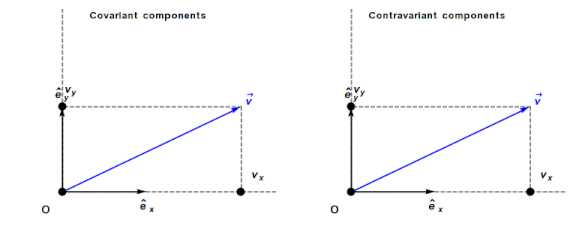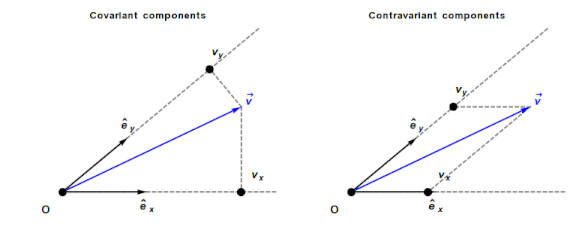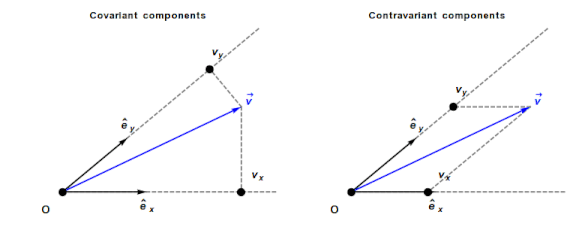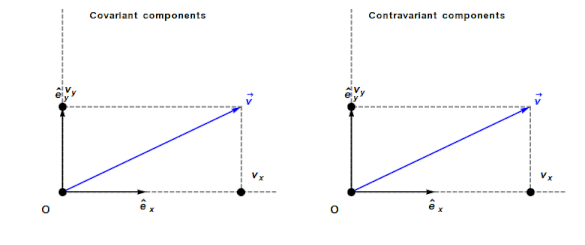
An understanding of General relativity requires an understanding of Tensor calculus, which in turn requires understanding the contravariant and covariant components of a vector. In the Cartesian coordinates system, which pervades undergraduate physics, the axes are at right angles and the measurement units are constant. The covariant component of a vector is the same as the contravariant component.
Contravariant/covariant vectors are different when the axes are not at right angles, as the plot below (from Wikipedia), shows. Choosing one component of the blue vector, the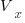 
component of its contravariant vector is measured by drawing a line parallel to the y-axis (on right), while the 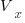component of its covariant vector is found by drawing a line perpendicular to the x-axis (on left). The plot below shows how the measurements of each component vary as the angle between the x/y axes varies:
Susskind’s definition of covariant vectors is a differential equation, which might be enough for some people, but not me. Boyes gives a very clear description (he does labour points, and I watched at 1.75 speed).
There are other places where I found Boyes’ explanation to be clearer, and a few where I preferred Susskind. I would recommend both.
What complicates the use of Tensor calculus is the multiplicity of terms in an equation. In 3-dimensional Cartesian coordinates there are three variables x/y/z, while in 3-dimensional Tensor calculus there are nine variables (the coordinate system can produce an interaction between any axis and another one). 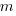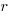The equation for the proper acceleration of an object, written using the Einstein summation convention (there is a summation over the repeated indexes, 
, 
, 
) is: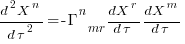 
. In three dimensions, there would be three equations (i.e., 
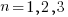), each with nine terms on the right, for 
, 
; 
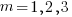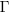is the Christoffel symbol which calculates the unit distance for a location in space (in Cartesian coordinates this simplifies down to what we all learned in school); the superscripts denote contravariant components, and the subscripts denote covariant components:
How did Einstein derive his field equation,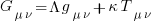 
, of General relativity?
I had known of the equivalence principle, that the force experienced by an accelerating observer (e.g., travelling in an elevator) is indistinguishable from the force of gravity, but had not appreciated how this principle played an integral part in the derivation of the equations for the force experienced in a gravitational field.
The derivation is based on asking about the trajectory of a rocket accelerating at a constant rate in a flat space-time (allowing Cartesian coordinates to be used). If a stationary observer on the ground tracks the rocket from when it starts with zero velocity and then constantly accelerates in a straight line for a very long time, how will the velocity and distance of the rocket (from the observer) change over time? From the ground-based observer’s perspective, the rocket’s velocity will get closer and closer to the speed of light; Special relativity prevents it exceeding the speed of light. The distance travelled by the rocket over time, as tracked by the ground-based observer, will be seen to be fitted by a hyperbolic equation. This analysis is used to justify the use of hyperbolic geometric as a coordinate system for dealing with gravity.
A hyperbolic metric space was not enough for Einstein to derive his equations. He also assumed conservation of various quantities, and appears to have included some idealism about how the Universe ought to operate.
Special relativity predicts some very surprising behaviors, such as of time dilation. What very surprising behaviours does General relativity predict?
The bending of light by gravity is often cited as an example of a prediction by General relativity. However, bending is predicted my Newtonian mechanics, but the amount is half that predicted by General relativity.
While Black holes get a lot of public attention, and are discussion time by Susskind and Boyes, General relativity is not needed to make the prediction that that gravitational attraction of a sufficiently massive body will be greater than the speed of light.
General relativity deals with accelerating frames of reference (gravity or rocket ships). Both Susskind and Boyes discuss some version of Bell’s spaceship paradox, which is actually a consequence of Special relativity; I think that Boyes YouTube video is the easiest to follow.
Apart from ticking another item on my to-do list, I now appreciate some of the subtle points people make about General relativity. I’m sure that this knowledge will increase the likelihood of me getting in over my head in some future discussion on relativity.
Distribution of program sizes
Program size, in lines of code (LOC), used to be a topic of conversation among developers and managers. Program size is an issue when computer memory is measured in kilobytes. Large programs would be organized into overlays such that only small subsets needed to be held in memory at any time, i.e., programmer defined memory management.
Management used program size as a proxy for implementation effort/cost. Because size was a topic of conversation, it was possible to ask around to obtain a selection of values for the size of programs with similar functionality (accurate actual implementation costs were/are rarely available via the grapevine, but developers were/are always happy to talk about how small/large their programs were/are). These days, estimating LOC prior to implementation may appear more scientific, but I doubt it’s more accurate.
Once computers containing megabytes of memory became widespread, and the use of third-party libraries continued to grow, program size became a niche topic of conversation.
The size of some operating systems has become an occasional topic of conversation; it wasn’t previously because mainframe/mini computer manufacturers didn’t want customers talking about how much of their expensive memory was taken up by the OS. The size of Microsoft Windows leaked out and the Linux kernel is a topic of research.
Discussions around size have moved on from individual programs to the amount of space taken up by an installed application suite. Today, program size can be a rounding error compared to data files, extensions and add-ons.
Researchers have also moved on; repository size, in LOC/packages, is what now gets reported.
For those who are interested in program size; what is the distribution of program sizes? How many LOC are needed for a program to be above 50%, or in the top 95%?
Recent data on the size of individual programs is surprisingly hard to find, given how often LOC values appear in print. The one dataset I found is from the paper Empirical analysis of the relationship between CC and SLOC in a large corpus of Java methods and C functions, which is derived from the 2010’ish Sourcerer corpus of 13,103 Java projects (each of which I assume contains one program). The plot below shows the LOC (red) and methods (blue/green) for each program, in ascending order, along with values at various percentage points (code+data):
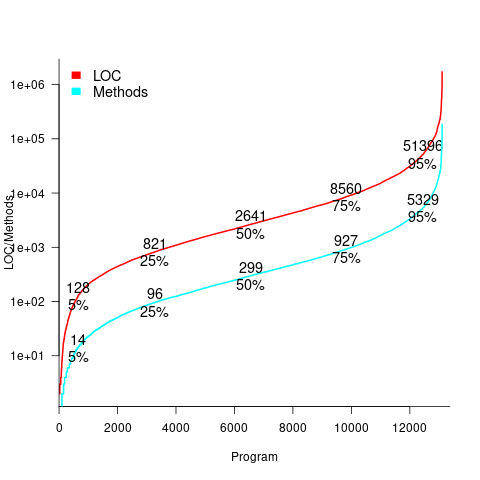
The size of Java programs is very likely to have increased since 2010. How much have grown? I don’t know.
What about the size of programs written in other languages?
I expect Python program size to be smaller, because the huge number of available package removes the need to implement a myriad of boilerplate functionality.
I expect C program size to be larger, both because of the smaller library ecosystem and because C programs tend to be older (programs rarely shrink with age).
Quantity of source in a given language
How much source code exists in a particular language?
Traditionally, indicators of the quantity of source in a language is the number of people making a living working on software written in the language. Job adverts are a proxy for the number of people employed to write/support programs implemented in a language (i.e., number of times a language is specified in the text of an advert), another proxy used to be the financial wellbeing of compiler vendors (many years ago, Open source compilers drove most companies out of the business of selling compilers).
Current job adverts are a measure of the code that likely to be worked now and in the near future. While Cobol dominated the job adverts decades ago, it is only occasionally seen today, suggesting that a lot of Cobol source is no longer actively used.
There now exists a huge quantity of Open source, and it has permeated into all the major, and many minor, software ecosystems. As a measure of all existing source code, how representative is Open source?
The Software Heritage’s mission statement “… is to collect, preserve, and share all software that is publicly available in source code form.” With over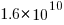 
files, as of July 2023 it is the largest available collection of Open source, and furthermore the BigCode project has collated this source into 658 constituent languages, known the Stack version 2.
To be representative of all existing source code, the Stack v2 would need to contain a representative sample of source written in all the languages that have been used to implement a non-trivial quantity of code. The plot below shows the number of source files assumed to be from a given year, storage by the Software Heritage; green lines are fitted exponentials (code+data):
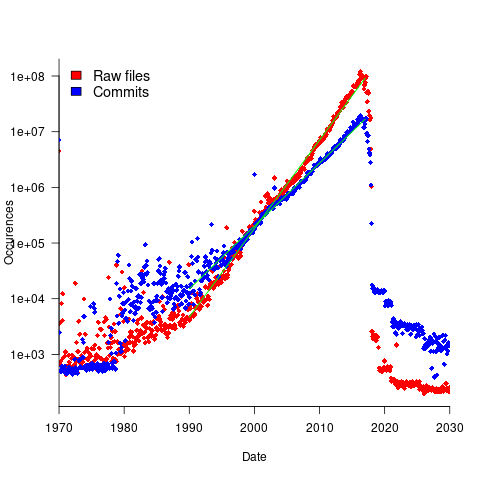
Less Open source was written in years gone by because there were fewer developers writing code, and code tends to get lost.
The Wikipedia list of programming languages currently contains links to articles on 682 languages, although some entries do appear to stretch the definition of programming language, e.g., Geometric Description Language. The Stack v2 contains code in 658 languages. However, even the broadest definition of programming language would not include some of the entries, e.g., Vim Help File. There are 176 language names shared between lists (around 27%; code+data).
Wikipedia languages not contained in Stack v2 include dialects of Basic, C, Lisp, Pascal, and shell, along with languages I recognised. Stack v2 languages not contained in the Wikipedia list include a variety of build and configuration files, names I did not recognise and what looked like documentation and data files.
Stack v2 has a broad brush approach to language classification. There is only one Pascal (perhaps the most widely used language in the early days of the IBM PC, Turbo Pascal, does not get a mention, and neither does UCSD Pascal), and assembler languages can vary a lot between cpus (Stack v2 lists: Assembly, Motorola 68K Assembly, Parrot Assembly, WebAssembly, Unix Assembly).
The Online Historical Encyclopaedia of Programming Languages lists information on 8,945 languages. Most of these probably got no further than being implemented in themselves by the language designer (often for a PhD thesis).
The Stack v2’s definition of a non-trivial quantity is at least 1,000 files having a given filename suffix, e.g., .cpp denoting C++ source. I can understand that this limit might exclude some niche languages from long ago (e.g., Coral 66), but why isn’t there any Algol 60 source?
I suspect that many ‘earlier’ languages are not included because the automated source submission process requires that the code be accessible via one of five version control systems. A lot of older source is stored in tar/zip files, accessed via ftp directories or personal web pages. Software Heritage’s Collect and Curate Legacy Code does not yet appear to provide a process for submitting source available in these forms.
While I think that Open source code has the same language usage characteristics as Closed source, I continue to meet people who question this assumption. I doubt that the question will ever get a definitive answer, not least because of an unwillingness to invest the resources needed to do a large sample comparison.
I would expect there to be at least 100 times as much Closed source as Open source, if only because there are a lot more people writing Closed source.
Obtaining source code for training LLMs
Training a large language model to be a coding assistant requires huge amounts of source code.
Github is a very well known publicly available repository of code, and various sites have created substantial collections of GitHub repos, e.g., GitTorrent, and Google’s BigQuery. Since 2017 the Software Heritage has been amassing the world’s source code, and now looks like it will become the default site for those seeking LLM source code training data. The benefits of using the Software_Heritage, include:
- deduplication at the file level for free. Files are organized using a cryptographic hash of their contents (i.e., a Merkle tree), which is user visible. GitHub may deduplicate internally, but the user visible data structure is based on individual repositories. One study found that 70% of code on GitHub are clones. Deduplication has been a major housekeeping task when creating a source code training dataset.
A single space character or newline is enough to cause a cryptographic hash to change and a file to be treated as different. Studies of file contents has found them differing by the presence/absence of a license at the start of the file, and other non-consequential differences. The LLM training dataset “The Stack v2” has further deduplicated the Software Heritage dataset, removing over 50% of files,
- accessed using AWS. The 11TiB of data can be bulk downloaded from the S3 bucket s3://softwareheritage/graph/. An Amazon Athena hosted version of the dataset can be queried using the Presto distributed SQL engine (filename suffix could be used to extract files likely to contain source in particular languages). Amazon also have an Azure Databricks hosted version.
Suggestions for the best way of accessing this data, for LLM training, welcome,
- Software_Heritage hosts more code than GitHub, although measurements from late 2021 suggests that at the time, over 95% originated on GitHub.
StarCoder2, released at the end of February, is an open weights model trained in partnership with the Software Heritage (a year ago, version 1 of StarCoder was trained using an order of magnitude less source).
How much source is available via the Software Heritage?
As of July 2023 the site hosted 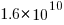files.
Let’s assume 64 lines per file, and 26 non-whitespace characters per line, giving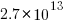 
non-whitespace characters. How many tokens is this?
The most common statement is assignment, which typically contains 4 language tokens (e.g., a = b ; ). There is an exponential decline in language tokens per line (Fig 770.17). The question is how many LLM tokens per computer language identifier, which tend to be abbreviated; I have no idea how these map to LLM tokens.
Assuming 10 LLM tokens per line, we get: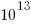 
LLM tokens; this is 2.7 non-whitespace characters per token, which feels about right.
The Stack v2 Hugging Face page lists the deduplicated dataset as containing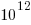 
tokens. However, they only include files in the main branch (the Software Heritage dataset includes files containing branches and commits), and the total number of files in the full Stack v2 dataset is 
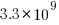, with the deduped training dataset containing 
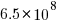files (they do not train using copyleft files, which are approximately 20-25% of the files on GitHub).
My calculation probably overestimated the number of tokens on a line. LLM’s specifically trained on source code have tokenisers optimized for the characteristics of code, e.g., allowing tokens to span whitespace to allow for idioms such as import numpy as np to be treated as single tokens.
Given the exponential growth of files available on the Software Heritage, it is possible that several orders of magnitude more tokens will eventually become available.
Licensing, in the form of the GPL, is a complication that hangs over the use of some public source code (maybe 25%). An ongoing class-action suit will likely take years to resolve, and it’s possible that model training will have improved to the extent that any loss of GPL’d code will not seriously impact model performance:
- When source is licensed under the GNU General Public License, do models that use it during training have themselves to be released under a GPL license? In November 2022 a class-action lawsuit was filed, challenging the legality of GitHub Copilot and related OpenAI products. This case has yet to reach jury trial, and after that there will no doubt be appeals. The resolution is years in the future,
- if the plaintiffs win, with models trained using GPL’d code required to release the weights under a GPL license. The different source files used to build a project sometimes have different, incompatible, Open source licenses. LLM training does not require complete sets of project source files, so the presence of GPL’d source is not contagious within a project. If the same file appears with different licenses, one of which is the GPL, the simplest option may be to exclude it. One study found the GPL-3 license present under 2,871 different filenames.
Given that around 50% of GitHub repos don’t specify any license, and around 30% specify an MIT license, not using GPL’d code for training does not look like it will affect the training of general coding models. However, these models will have problems dealing with issues that require interfacing to GPL’d code.
Recent Comments