Perturbed expressions may ‘recover’
This week I have been investigating the impact of perturbing the evaluation of random floating-point expressions. In particular, the impact of adding 1 (and larger values) at a random point in an expression containing many binary operators (simply some combination of add/multiply).
What mechanisms make it possible for the evaluation of an expression to be unchanged by a perturbation of +1.0 (and much larger values)? There are two possible mechanisms:
- the evaluated value at the perturbation point is ‘watered down’ by subsequent operations, such that the original perturbed value makes no contribution to the final result. For instance, the IEEE single precision float mantissa is capable of representing 6-significant digits; starting with, say, the value
0.23, perturbing by adding1.0gives1.23, followed by a sequence of many multiplications by values between zero and one could produce, say, the value6.7e-8, which when added to, say,0.45, gives0.45, i.e., the perturbed value is too small to affect the result of the add, - the perturbed branch of the expression evaluation is eventually multiplied by zero (either because the evaluation of the other branch produces zero, or the operand happens to be zero). The exponent of an IEEE single precision float can represent values as small as
1e-38, before underflowing to zero (ignoring subnormals); something that is likely to require many more multiplies than required to lose 6-significant digits.
The impact of a perturbation disappears when its value is involved in a sufficiently long sequence of repeated multiplications.
The probability that the evaluation of a sequence of  multiplications of random values uniformly distributed between zero and one produces a result less than
multiplications of random values uniformly distributed between zero and one produces a result less than  is given by
is given by 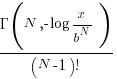 , where
, where  is the incomplete gamma function, and
is the incomplete gamma function, and  is the upper bounds (1 in our case). The plot below shows this cumulative distribution function for various
is the upper bounds (1 in our case). The plot below shows this cumulative distribution function for various  (code):
(code):
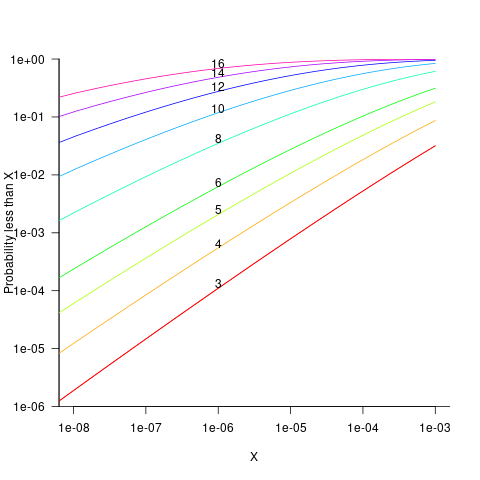
Looking at this plot, a sequence of 10 multiplications has around a 1-in-10 chance of evaluating to a value less than 1e-6.
In practice, the presence of add operations will increase the range of operands values to be greater than one. The expected distribution of result values for expressions containing various percentages of add/multiply operators is covered in an earlier post.
The probability that the evaluation of an expression involves a sequence of  multiplications depends on the percentage of multiply operators it contains, and the shape of the expression tree. The average number of binary operator evaluations in a path from leaf to root node in a randomly generated tree of
multiplications depends on the percentage of multiply operators it contains, and the shape of the expression tree. The average number of binary operator evaluations in a path from leaf to root node in a randomly generated tree of  operands is proportional to
operands is proportional to 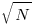 .
.
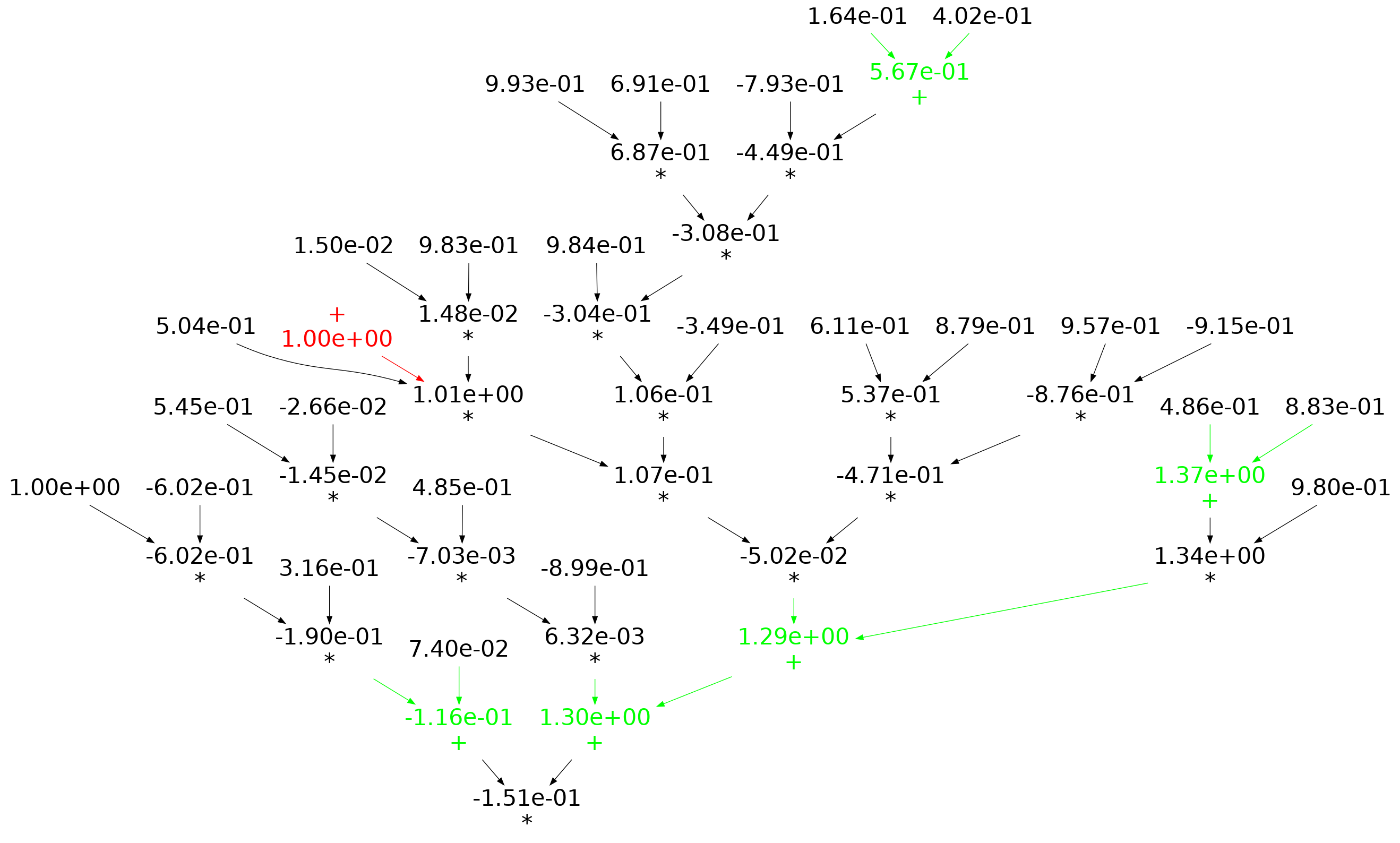
When an expression has a ‘bushy’ balanced form, there are many relatively distinct evaluation paths, the expected number of operations along a path is proportional to 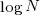 . The plot below shows a randomly generated ‘bushy’ expression tree containing 25 binary operators, with 80% multiply, and randomly selected values (perturbation in red, additions in green; code+data):
. The plot below shows a randomly generated ‘bushy’ expression tree containing 25 binary operators, with 80% multiply, and randomly selected values (perturbation in red, additions in green; code+data):
When an expression has a ‘tall’ form, there is one long evaluation path, with a few short paths hanging off it, the expected number of operations along the long path is proportional to  . The plot below shows a randomly generated ‘tall’ expression tree containing 25 binary operators, with 80% multiply, and randomly selected values (perturbation in red, additions in green; code+data):
. The plot below shows a randomly generated ‘tall’ expression tree containing 25 binary operators, with 80% multiply, and randomly selected values (perturbation in red, additions in green; code+data):

If, one by one, the result of every operator in an expression is systematically perturbed (by adding some value to it), it is known that in some cases the value of the perturbed expression is the same as the original.
The following results were obtained by generating 200 random C expressions containing some percentage of add/multiply, some number of operands (i.e., 25, 50, 75, 100, 150), one-by-one perturbing every operator in every expression, and comparing the perturbed result value to the original value. This process was repeated 200 times, each time randomly selecting operand values from a uniform distribution between -1 and 1. The perturbation values used were: 1e0, 1e2, 1e4, 1e8, 1e16. A 32-bit float type was used throughout.
Depending on the shape of the expression tree, with 80% multiplications and 100 operands, the fraction of perturbed expressions returning an unchanged value can vary from 1% to 40%.
The regression model fitted to the fraction of unchanged expressions contains lots of interactions (the simple version is that the fraction unchanged increases with more multiplications, decreases as the log of the perturbation value, the square root of the number of operands is involved; code+data):
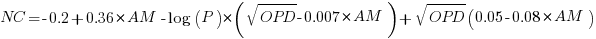
where: 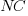 is the fraction of perturbed expressions returning the original value,
is the fraction of perturbed expressions returning the original value, 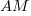 the percentage of add operators (not multiply),
the percentage of add operators (not multiply), 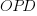 the number of operands in the expression, and
the number of operands in the expression, and 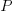 the perturbation value.
the perturbation value.
There is a strong interaction with the shape of the expression tree, but I have not found a way of integrating this into the model.
The following plot shows the fraction of expressions unchanged by adding one, as the perturbation point moves up a tall tree, x-axis, for expressions containing 50 and 100 operands, and various percentages of multiplications (code+data):
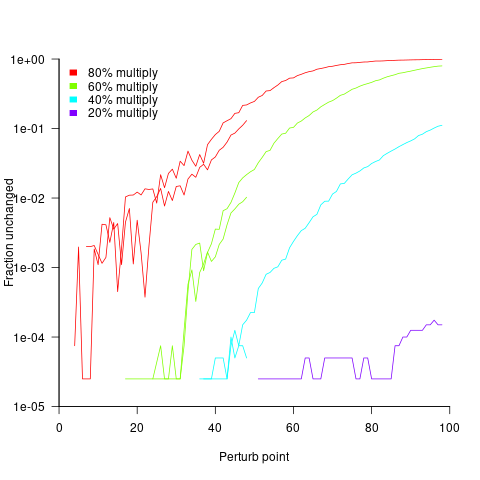
No attempt was made to count the number of expression evaluations where the perturbed value was eventually multiplied by zero (the second bullet point discussed at the start).
A special case where perturbing a value by +1 has no effect occurs in systems that implement saturated integer arithmetic. Matlab is an exemplar. See https://docs.julialang.org/en/v1/manual/faq/#faq-integer-arithmetic for a discussion.