Analysis of when refactoring becomes cost-effective
In a cost/benefit analysis of deciding when to refactor code, which variables are needed to calculate a good enough result?
This analysis compares the excess time-code of future work against the time-cost of refactoring the code. Refactoring is cost-effective when the reduction in future work time is less than the time spent refactoring. The analysis finds a relationship between work/refactoring time-costs and number of future coding sessions.
Linear, or supra-linear case
Let’s assume that the time needed to write new code grows at a linear, or supra-linear rate, as the amount of code increases (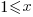 ):
):
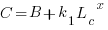
where: 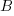 is the base time for writing new code on a freshly refactored code base,
is the base time for writing new code on a freshly refactored code base, 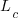 is the number of lines of code that have been written since the last refactoring, and
is the number of lines of code that have been written since the last refactoring, and 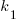 and
and  are constants to be decided.
are constants to be decided.
The total time spent writing code over  sessions is:
sessions is:
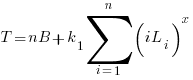
If the same number of new lines is added in every coding session, 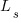 , and
, and  is an integer constant, then the sum has a known closed form, e.g.:
is an integer constant, then the sum has a known closed form, e.g.:
x=1, 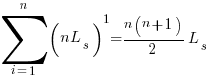 ; x=2,
; x=2, 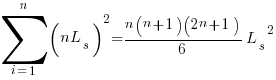
Let’s assume that the time taken to refactor the code written after  sessions is:
sessions is:
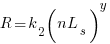
where:  and
and  are constants to be decided.
are constants to be decided.
The reason for refactoring is to reduce the time-cost of subsequent work; if there are no subsequent coding sessions, there is no economic reason to refactor the code. If we assume that after refactoring, the time taken to write new code is reduced to the base cost,  , and that we believe that coding will continue at the same rate for at least another
, and that we believe that coding will continue at the same rate for at least another  sessions, then refactoring existing code after
sessions, then refactoring existing code after  sessions is cost-effective when:
sessions is cost-effective when:
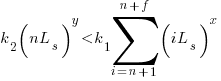
assuming that  is much smaller than
is much smaller than  , setting
, setting  , and rearranging we get:
, and rearranging we get:
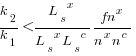
after rearranging we obtain a lower limit on the number of future coding sessions,  , that must be completed for refactoring to be cost-effective after session
, that must be completed for refactoring to be cost-effective after session  ::
::
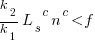
It is expected that 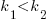 ; the contribution of code size, at the end of every session, in the calculation of
; the contribution of code size, at the end of every session, in the calculation of  and
and 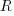 is equal (i.e.,
is equal (i.e., 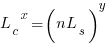 ), and the overhead of adding new code is very unlikely to be less than refactoring all the newly written code.
), and the overhead of adding new code is very unlikely to be less than refactoring all the newly written code.
With 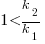 ,
,  must be close to zero; otherwise, the likely relatively large value of
must be close to zero; otherwise, the likely relatively large value of 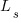 (e.g., 100+) would produce surprisingly high values of
(e.g., 100+) would produce surprisingly high values of  .
.
Sublinear case
What if the time overhead of writing new code grows at a sublinear rate, as the amount of code increases?
Various attributes have been found to strongly correlate with the 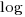 of lines of code. In this case, the expressions for
of lines of code. In this case, the expressions for  and
and 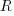 become:
become:
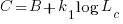
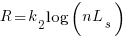
and the cost/benefit relationship becomes:

applying Stirling’s approximation and simplifying (see Exact equations for sums at end of post for details) we get:
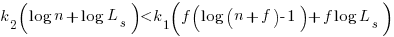
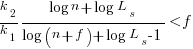
applying the series expansion (for 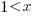 ):
): 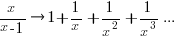 , we get
, we get
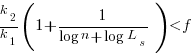
Discussion
What does this analysis of the cost/benefit relationship show that was not obvious (i.e., the relationship 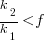 is obviously true)?
is obviously true)?
What the analysis shows is that when real-world values are plugged into the full equations, all but two factors have a relatively small impact on the result.
A factor not included in the analysis is that source code has a half-life (i.e., code is deleted during development), and the amount of code existing after  sessions is likely to be less than the
sessions is likely to be less than the 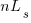 used in the analysis (see Agile analysis).
used in the analysis (see Agile analysis).
As a project nears completion, the likelihood of there being  more coding sessions decreases; there is also the every present possibility that the project is shutdown.
more coding sessions decreases; there is also the every present possibility that the project is shutdown.
The values of 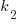 and
and 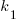 encode information on the skill of the developer, the difficulty of writing code in the application domain, and other factors.
encode information on the skill of the developer, the difficulty of writing code in the application domain, and other factors.
Exact equations for sums
The equations for the exact sums, for 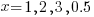 , are:
, are:
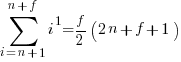
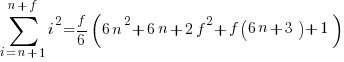
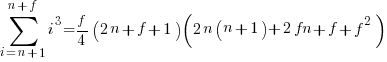
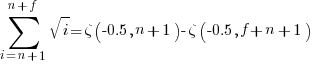 , where
, where 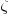 is the Hurwitz zeta function.
is the Hurwitz zeta function.
Sum of a log series: 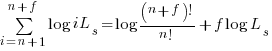
using Stirling’s approximation we get
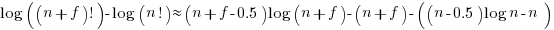
simplifying
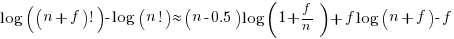
and assuming that  is much smaller than
is much smaller than  gives
gives
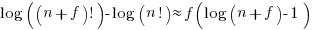
Recent Comments