The Shape of Code

Recommendations for/against particular programming constructs have one thing in common: there is no evidence backing up any of the recommendations. Running experiments to measure the impact of particular language features on developer performance is not something that researchers do (there have been a handful of experiments looking at the impact of strong typing on developer performance; the effect measured was tiny).

In February I discovered two groups researching regular expressions. In the first post on duplicate regexs, I promised to say something about the second group. This post discusses an experiment comparing developer comprehension of various regular expressions; the paper is: Exploring Regular Expression Comprehension.

The experiment involved 180 workers on Mechanical Turk (to be accepted, workers had to correctly answer four or five questions about regular expressions). Workers/subjects performed two different tasks, matching and composition.

• In the matching task workers saw a regex and a list of five strings, and had to specify whether the regex matched (or not) each string (there was also an unsure response).
• In the composition task workers saw a regular expression, and had to create a string matched by this regex. Each worker saw 10 different regexs, which were randomly drawn from a set of 60 regexs (which had been created to be representative of various regex characteristics). I have not analysed this data yet.

What were the results?

For the matching task: given each of the pairs of regexs below, which one (of each pair) would you say workers were most likely to get correct?

         R1                  R2
1.     tri[a-f]3         tri[abcdef]3
2.     no[w-z]5          no[wxyz]5
3.     no[w-z]5          no(w|x|y|z)5
4.     [ˆ0-9]            [\D]

The percentages correct for (1) were essentially the same, at 94.0 and 93.2 respectively. The percentages for (2) were 93.3 and 87.2, which is odd given that the regex is essentially the same as (1). Is this amount of variability in subject response to be expected? Is the difference caused by letters being much less common in text, so people have had less practice using them (sounds a bit far-fetched, but its all I could think of). The percentages for (3) are virtually identical, at 93.3 and 93.7.

The percentages for (4) were 58 and 73.3, which surprised me. But then I have been using regexs since before \D support was generally available. The MTurk generation have it easy not having to use the ‘hard stuff’ 😉

See Table III in the paper for more results.

This matching data might be analysed using Item Response theory, which can take into account differences in question difficulty and worker/subject ability. The plot below looks complicated, but only because there are so many lines. Each numbered colored line is a different regex, worker ability is on the x-axis (greater ability on the right), and the y-axis is the probability of giving a correct answer (code+data; thanks to Peipei Wang for fixing the bugs in my code):

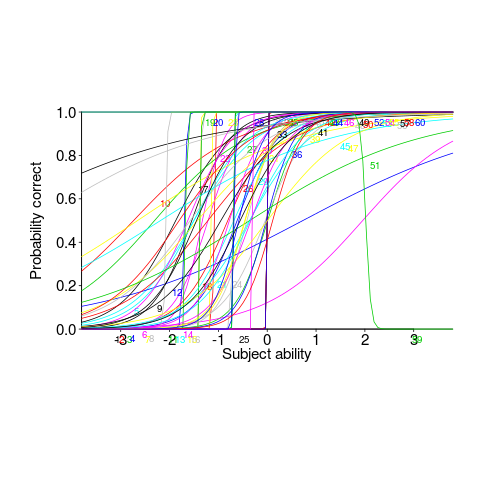
Yes, for question 51 the probability of a correct answer decreases with worker ability. Heads are being scratched about this.

There might be some patterns buried in amongst all those lines, e.g., particular kinds of patterns require a given level of ability to handle, or correct response to some patterns varying over the whole range of abilities. These are research questions, and this is a blog article: answers in the comments 🙂

This is the first experiment of its kind, so it is bound to throw up more questions than answers. Are more incorrect responses given for longer regexs, particularly if they cannot be completely held in short-term memory? It is convenient for the author to use a short-hand for a range of characters (e.g., a-f), and I was expecting a difference in performance when all the letters were enumerated (e.g., abcdef); I had theories for either one being less error-prone (I obviously need to get out more).