Archive
How are C functions different from Java methods?
According to the right plot below, most of the code in a C program resides in functions containing between 5-25 lines, while most of the code in Java programs resides in methods containing one line (code+data; data kindly supplied by Davy Landman):
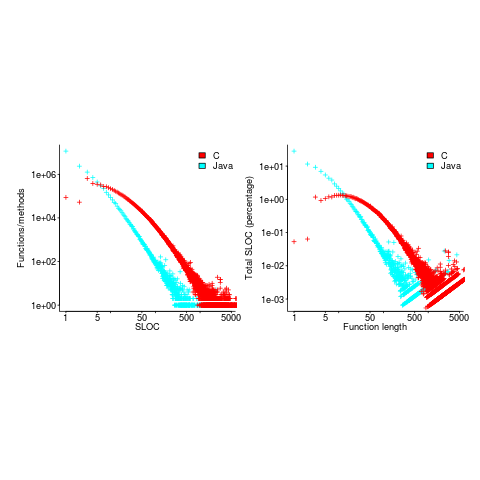
The left plot shows the number of functions/methods containing a given number of lines, the right plot shows the total number of lines (as a percentage of all lines measured) contained in functions/methods of a given length (6.3 million functions and 17.6 million methods).
Perhaps all those 1-line Java methods are really complicated. In C, most lines contain a few tokens, as seen below (code+data):
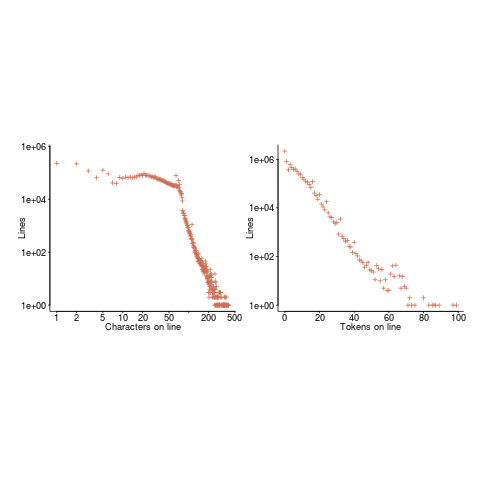
I don’t have any characters/tokens per line data for Java.
Is Java code mostly getters and setters?
I wonder what pattern C++ will follow, i.e., C-like, Java-like, or something else? If you have data for other languages, please send me a copy.
How useful are automatically generated compiler tests?
Over the last decade, testing compilers using automatically generated source code has been a popular research topic (for those working in the compiler field; Csmith kicked off this interest). Compilers are large complicated programs, and they will always contain mistakes that lead to faults being experienced. Previous posts of mine have raised two issues on the use of automatically generated tests: a financial issue (i.e., fixing reported faults costs money {most of the work on gcc and llvm is done by people working for large companies}, and is intended to benefit users not researchers seeking bragging rights for their latest paper), and applicability issue (i.e., human written code has particular characteristics and unless automatically generated code has very similar characteristics the mistakes it finds are unlikely to commonly occur in practice).
My claim that mistakes in compilers found by automatically generated code are unlikely to be the kind of mistakes that often lead to a fault in the compilation of human written code is based on the observations (I don’t have any experimental evidence): the characteristics of automatically generated source is very different from human written code (I know this from measurements of lots of code), and this difference results in parts of the compiler that are infrequently executed by human written code being more frequently executed (increasing the likelihood of a mistake being uncovered; an observation based on my years working on compilers).
An interesting new paper, Compiler Fuzzing: How Much Does It Matter?, investigated the extent to which fault experiences produced by automatically generated source are representative of fault experiences produced by human written code. The first author of the paper, Michaël Marcozzi, gave a talk about this work at the Papers We Love workshop last Sunday (videos available).
The question was attacked head on. The researchers instrumented the code in the LLVM compiler that was modified to fix 45 reported faults (27 from four fuzzing tools, 10 from human written code, and 8 from a formal verifier); the following is an example of instrumented code:
warn ("Fixing patch reached"); if (Not.isPowerOf2()) { if (!(C-> getValue().isPowerOf2() // Check needed to fix fault && Not != C->getValue())) { warn("Fault possibly triggered"); } else { /* CODE TRANSFORMATION */ } } // Original, unfixed code |
The instrumented compiler was used to build 309 Debian packages (around 10 million lines of C/C++). The output from the builds were (possibly miscompiled) built versions of the packages, and log files (from which information could be extracted on the number of times the fixing patches were reached, and the number of cases where the check needed to fix the fault was triggered).
Each built package was then checked using its respective test suite; a package built from miscompiled code may successfully pass its test suite.
A bitwise compare was run on the program executables generated by the unfixed and fixed compilers.
The following (taken from Marcozzi’s slides) shows the percentage of packages where the fixing patch was reached during the build, the percentages of packages where code added to fix a fault was triggered, the percentage where a different binary was generated, and the percentages of packages where a failure was detected when running each package’s tests (0.01% is one failure):
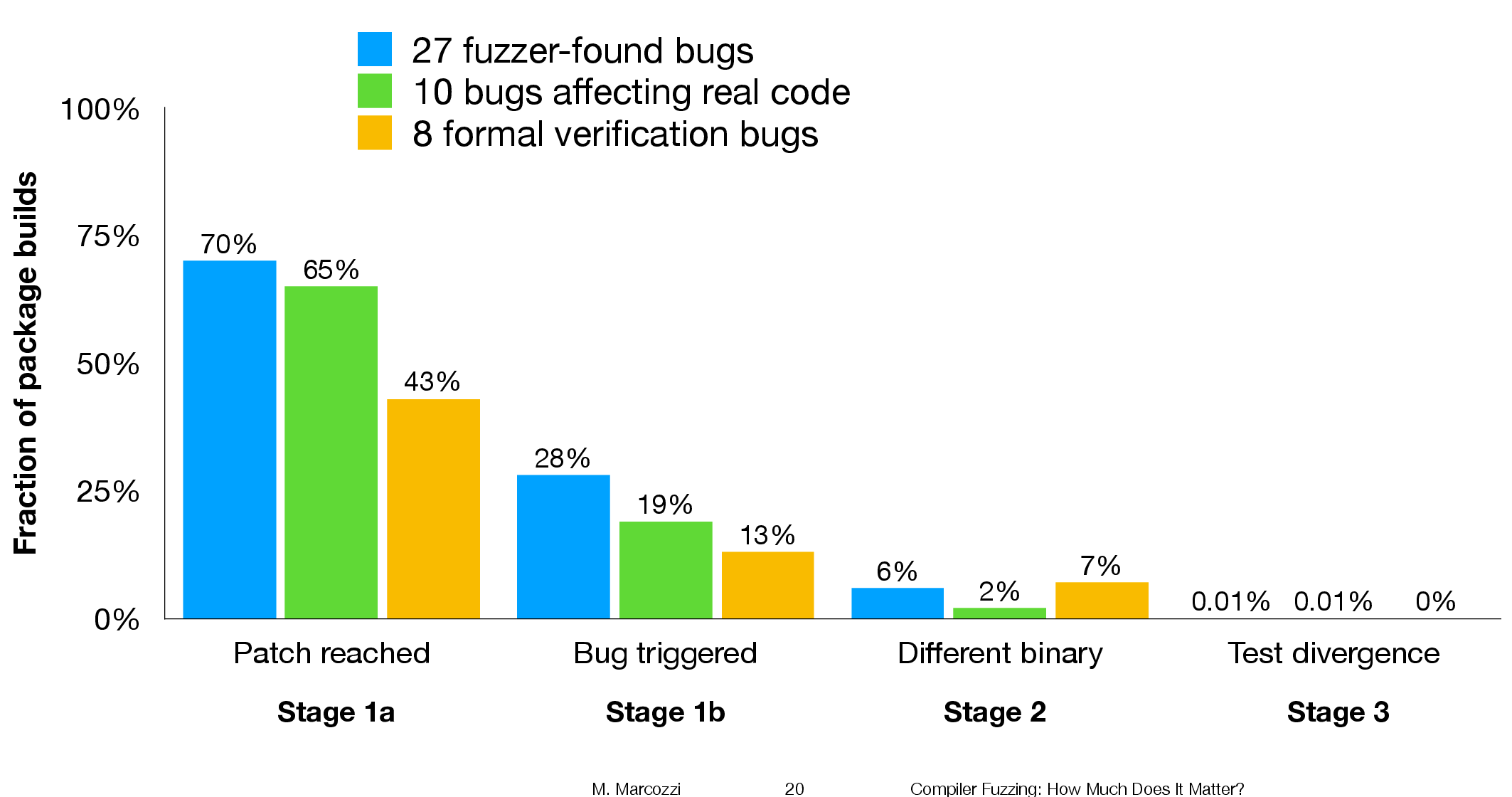
The takeaway from the above figure is that many packages are affected by the coding mistakes that have been fixed, but that most package test suites are not affected by the miscompilations.
To find out whether there is a difference, in terms of impact on Debian packages, between faults reported in human and automatically generated code, we need to compare the number of occurrences of “Fault possibly triggered”. The table below shows the break-down by the detector of the coding mistake (i.e., Human and each of the automated tools used), and the number of fixed faults they contributed to the analysis.
Human, Csmith and EMI each contributed 10-faults to the analysis. The fixes for the 10-fault reports in human generated code were triggered 593 times when building the 309 Debian packages, while each of the 10 Csmith and EMI fixes were triggered 1,043 and 948 times respectively; a lot more than the Human triggers :-O. There are also a lot more bitwise compare differences for the non-Human fault-fixes.
Detector Faults Reached Triggered Bitwise-diff Tests failed Human 10 1,990 593 56 1 Csmith 10 2,482 1,043 318 0 EMI 10 2,424 948 151 1 Orange 5 293 35 8 0 yarpgen 2 608 257 0 0 Alive 8 1,059 327 172 0 |
Is the difference due to a few packages being very different from the rest?
The table below breaks things down by each of the 10-reported faults from the three Detectors.
Ok, two Human fault-fix locations are never reached when compiling the Debian packages (which is a bit odd), but when the locations are reached they are just not triggering the fault conditions as often as the automatic cases.
Detector Reached Triggered
Human
300 278
301 0
305 0
0 0
0 0
133 44
286 231
229 0
259 40
77 0
Csmith
306 2
301 118
297 291
284 1
143 6
291 286
125 125
245 3
285 16
205 205
EMI
130 0
307 221
302 195
281 32
175 5
122 0
300 295
297 215
306 191
287 10 |
It looks like I am not only wrong, but that fault experiences from automatically generated source are more (not less) likely to occur in human written code (than fault experiences produced by human written code).
This is odd. At best, I would expect fault experiences from human and automatically generated code to have the same characteristics.
Ideas and suggestions welcome.
Update: the morning after
I have untangled my thoughts on how to statistically compare the three sets of data.
The bootstrap is based on the idea of exchangeability; which items being measured might we consider to be exchangeable, i.e., being able to treat the measurement of one as being the equivalent to measuring the other.
In this experiment, the coding mistakes are not exchangeable, i.e., different mistakes can have different outcomes.
But we might claim that the detection of mistakes is exchangeable; that is, a coding mistake is just as likely to be detected by source code produced by an automatic tool as source written by a Human.
The bootstrap needs to be applied without replacement, i.e., each coding mistake is treated as being unique. The results show that for the sum of the Triggered counts (code+data):
- treating Human and Csmith as being equally likely to detect the same coding mistake, there is a 18% change of the Human results being lower than 593.
- treating Human and EMI as being equally likely to detect the same coding mistake, there is a 12% change of the Human results being lower than 593.
So the likelihood of the lower value, 593, of Human Triggered events is expected to occur quite often (i.e., 12% and 18%). Automatically generated code is not more likely to detect coding mistakes than human written code (at least based on this small sample set).
for-loop usage at different nesting levels
When reading code, starting at the first line of a function/method, the probability of the next statement read being a for-loop is around 1.5% (at least in C, I don’t have decent data on other languages). Let’s say you have been reading the code a line at a time, and you are now reading lines nested within various if/while/for statements, you are at nesting depth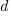 
. What is the probability of the statement on the next line being a for-loop?
Does the probability of encountering a for-loop remain unchanged with nesting depth (i.e., developer habits are not affected by nesting depth), or does it decrease (aren’t developers supposed to using functions/methods rather than nesting; I have never heard anybody suggest that it increases)?
If you think the for-loop use probability is not affected by nesting depth, you are going to argue for the plot on the left (below, showing number of loops whose compound-statement contains appearing in C source at various nesting depths), with the regression model fitting really well after 3-levels of nesting. If you think the probability decreases with nesting depth, you are likely to argue for the plot on the right, with the model fitting really well down to around 10-levels of nesting (code+data).
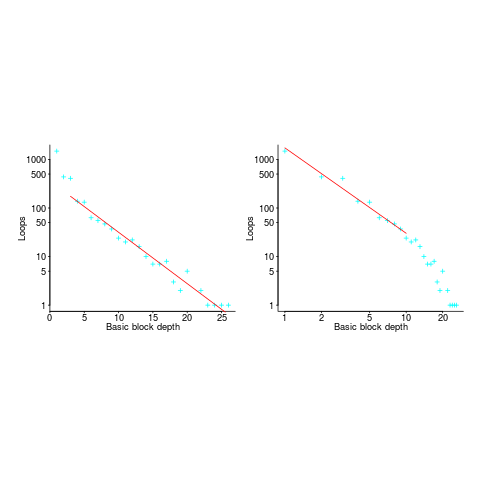
Both plots use the same data, but different scales are used for the x-axis.
If probability of use is independent of nesting depth, an exponential equation should fit the data (i.e., the left plot), decreasing probability is supported by a power-law (i.e, the right plot; plus other forms of equation, but let’s keep things simple).
The two cases are very wrong over different ranges of the data. What is your explanation for reality failing to follow your beliefs in for-loop occurrence probability?
Is the mismatch between belief and reality caused by the small size of the data set (a few million lines were measured, which was once considered to be a lot), or perhaps your beliefs are based on other languages which will behave as claimed (appropriate measurements on other languages most welcome).
The nesting depth dependent use probability plot shows a sudden change in the rate of decrease in for-loop probability; perhaps this is caused by the maximum number of characters that can appear on a typical editor line (within a window). The left plot (below) shows the number of lines (of C source) containing a given number of characters; the right plot counts tokens per line and the length effect is much less pronounced (perhaps developers use shorter identifiers in nested code). Note: different scales used for the x-axis (code+data).
I don’t have any believable ideas for why the exponential fit only works if the first few nesting depths are ignored. What could be so special about early nesting depths?
What about fitting the data with other equations?
A bi-exponential springs to mind, with one exponential driven by application requirements and the other by algorithm selection; but reality is not on-board with this idea.
Ideas, suggestions, and data for other languages, most welcome.
The dark-age of software engineering research: some evidence
Looking back, the 1970s appear to be a golden age of software engineering research, with the following decades being the dark ages (i.e., vanity research promoted by ego and bluster), from which we are slowly emerging (a rough timeline).
Lots of evidence-based software engineering research was done in the 1970s, relative to the number of papers published, and I have previously written about the quantity of research done at Rome and the rise of ego and bluster after its fall (Air Force officers studying for a Master’s degree publish as much software engineering data as software engineering academics combined during the 1970s and the next two decades).
What is the evidence for a software engineering research dark ages, starting in the 1980s?
One indicator is the extent to which ancient books are still venerated, and the wisdom of the ancients is still regularly cited.
I claim that my evidence-based software engineering book contains all the useful publicly available software engineering data. The plot below shows the number of papers cited (green) and data available (red), per year; with fitted exponential regression models, and a piecewise regression fit to the data (blue) (code+data).
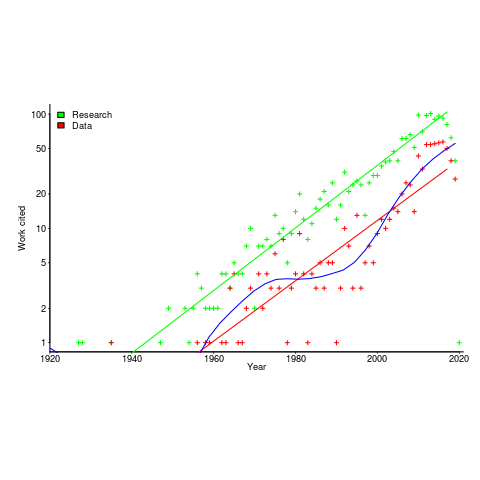
The citations+date include works that are not written by people involved in software engineering research, e.g., psychology, economics and ecology. For the time being I’m assuming that these non-software engineering researchers contribute a fixed percentage per year (the BibTeX file is available if anybody wants to do the break-down)
The two straight line fits are roughly parallel, and show an exponential growth over the years.
The piecewise regression (blue, loess was used) shows that the rate of growth in research data leveled-off in the late 1970s and only started to pick up again in the 1990s.
The dip in counts during the last few years is likely to be the result of me not having yet located all the recent empirical research.
Performance variation in 2,386 ‘identical’ processors
Every microprocessor is different, random variations in the manufacturing process result in transistors, and the connections between them, being fabricated with more/less atoms. An atom here and there makes very little difference when components are built from millions, or even thousands, of atoms. The width of the connections between transistors in modern devices might only be a dozen or so atoms, and an atom here and there can have a noticeable impact.
How does an atom here and there affect performance? Don’t all processors, of the same product, clocked at the same frequency deliver the same performance?
Yes they do, an atom here or there does not cause a processor to execute more/less instructions at a given frequency. But an atom here and there changes the thermal characteristics of processors, i.e., causes them to heat up faster/slower. High performance processors will reduce their operating frequency, or voltage, to prevent self-destruction (by overheating).
Processors operating within the same maximum power budget (say 65 Watts) may execute more/less instructions per second because they have slowed themselves down.
Some years ago I spotted a great example of ‘identical’ processor performance variation, and the author of the example, Barry Rountree, kindly sent me the data. In the weeks before Christmas I finally got around to including the data in my evidence-based software engineering book. Unfortunately I could not figure out what was what in the data (relearning an important lesson: make sure to understand the data as soon as it arrives), thankfully Barry came to the rescue and spent some time doing software archeology to figure out the data.
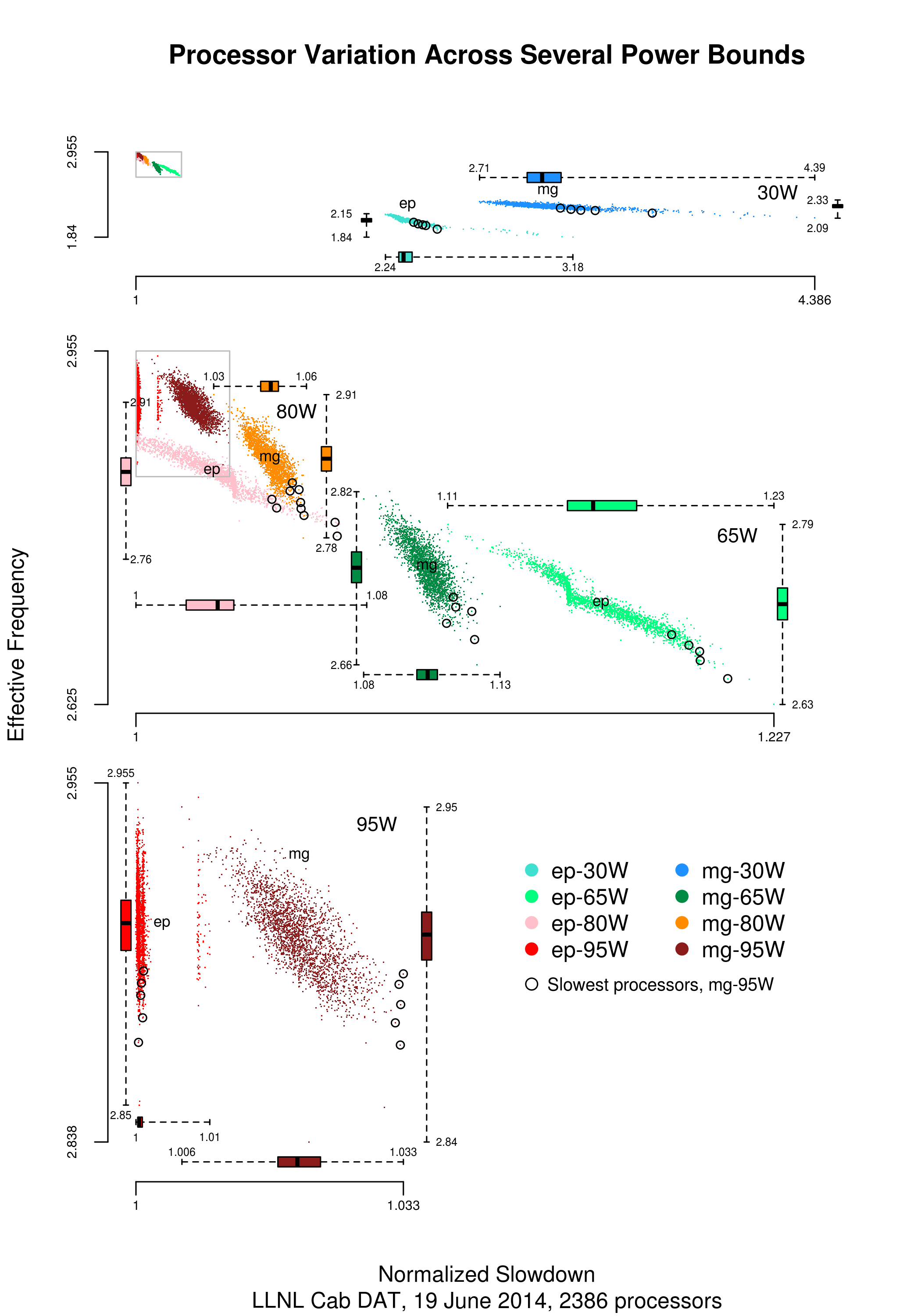
The original plots showed frequency/time data of 2,386 Intel Sandy Bridge XEON processors (in a high performance computer at the Lawrence Livermore National Laboratory) executing the EP benchmark (the data also includes measurements from the MG benchmark, part of the NAS Parallel benchmark) at various maximum power limits (see plot at end of post, which is normalised based on performance at 115 Watts). The plot below shows frequency/time for a maximum power of 65 Watts, along with violin plots showing the spread of processors running at a given frequency and taking a given number of seconds (my code, code+data on Barry’s github repo):
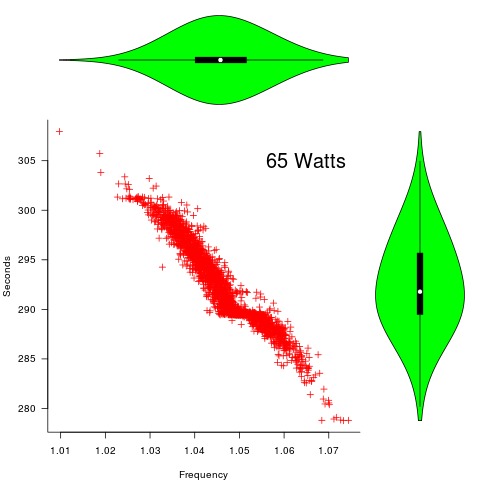
The expected frequency/time behavior is for processors to lie along a straight line running from top left to bottom right, which is roughly what happens here. I imagine (waving my software arms about) the variation in behavior comes from interactions with the other hardware devices each processor is connected to (e.g., memory, which presumably have their own temperature characteristics). Memory performance can have a big impact on benchmark performance. Some of the other maximum power limits, and benchmark, measurements have very different characteristics (see below).
More details and analysis in the paper: An empirical survey of performance and energy efficiency variation on Intel processors.
Intel’s Sandy Bridge is now around seven years old, and the number of atoms used to fabricate transistors and their connectors has shrunk and shrunk. An atom here and there is likely to produce even more variation in the performance of today’s processors.
A previous post discussed the impact of a variety of random variations on program performance.
Update start
A number of people have pointed out that I have not said anything about the impact of differences in heat dissipation (e.g., faster/slower warmer/cooler air-flow past processors).
There is some data from studies where multiple processors have been plugged, one at a time, into the same motherboard (i.e., low budget PhD research). The variation appears to be about the same as that seen here, but the sample sizes are more than two orders of magnitude smaller.
There has been some work looking at the impact of processor location (e.g., top/bottom of cabinet). No location effect was found, but this might be due to location effects not being consistent enough to show up in the stats.
Update end
Below is a png version of the original plot I saw:
Recent Comments