Calculating statement execution likelihood
In the following code, how often will the variable b be incremented, compared to a?
If we assume that the variables x and y have values drawn from the same distribution, then the condition (x < y) will be true 50% of the time (ignoring the situation where both values are equal), i.e., b will be incremented half as often as a.
a++; if (x < y) { b++; if (x < z) { c++; } } |
If the value of z is drawn from the same distribution as x and y, how often will c be incremented compared to a?
The test (x < y) reduces the possible values that x can take, which means that in the comparison (x < z), the value of x is no longer drawn from the same distribution as z.
Since we are assuming that z and y are drawn from the same distribution, there is a 50% chance that (z < y).
If we assume that (z < y), then the values of x and z are drawn from the same distribution, and in this case there is a 50% change that (x < z) is true.
Combining these two cases, we deduce that, given the statement a++; is executed, there is a 25% probability that the statement c++; is executed.
If the condition (x < z) is replaced by (x > z), the expected probability remains unchanged.
If the values of x, y, and z are not drawn from the same distribution, things get complicated.
Let's assume that the probability of particular values of x and y occurring are 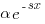 and
and 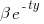 , respectively. The constants
, respectively. The constants 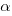 and
and 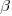 are needed to ensure that both probabilities sum to one; the exponents
are needed to ensure that both probabilities sum to one; the exponents 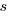 and
and 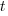 control the distribution of values. What is the probability that
control the distribution of values. What is the probability that (x < y) is true?
Probability theory tells us that 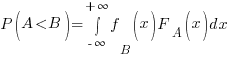 , where:
, where: 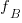 is the probability distribution function for
is the probability distribution function for 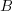 (in this case:
(in this case: 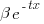 ), and
), and 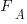 the cumulative probability distribution for
the cumulative probability distribution for 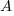 (in this case:
(in this case: 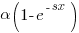 ).
).
Doing the maths gives the probability of (x < y) being true as: 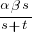 .
.
The (x < z) case can be similarly derived, and combining everything is just a matter of getting the algebra right; it is left as an exercise to the reader :-)
Recent Comments