Modeling visual studio C++ compile times
Last week I spotted an interesting article on the compile-time performance of C++ compilers running under Microsoft Windows. The author had obviously put a lot of work into gathering the data, and had taken care to have multiple runs to reduce the impact of random effects (128 runs to be exact); but, as if often the case, the analysis of the data was lackluster. I posted a comment asking for the data, and a link was posted the next day 🙂
The compilers benchmarked were: Visual Studio 2015, Visual Studio 2017 and clang 7.0.1; the compilers were configured to target: C++20, C++17, C++14, C++11, C++03, or C++98. The source code used was 100 system headers.
If we are interested in understanding the contribution of each component to overall compile-time, the obvious fist regression model to build is:
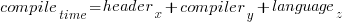
where: 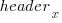 are the different headers,
are the different headers, 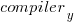 the different compilers and
the different compilers and 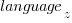 the different target languages. There might be some interaction between variables, so something more complicated was tried first; the final fitted model was (code+data):
the different target languages. There might be some interaction between variables, so something more complicated was tried first; the final fitted model was (code+data):
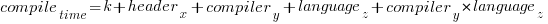
where 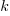 is a constant (the
is a constant (the Intercept in R’s summary output). The following is a list of normalised numbers to plug into the equation (clang is the default compiler and C++03 the default language, and so do not appear in the list, the : symbol represents the multiplication; only a few of the 100 headers are listed, details are available):
Estimate Std. Error t value Pr(>|t|) (Intercept) headerany 1.000000000 0.051100398 headerarray headerassert.h 0.522336397 -0.654056185 ... headerwctype.h headerwindows.h -0.648095154 1.304270250 compilerVS15 compilerVS17 -0.185795534 -0.114590143 languagec++11 languagec++14 0.032930014 0.156363433 languagec++17 languagec++20 0.192301727 0.184274629 languagec++98 compilerVS15:languagec++11 0.001149643 -0.058735591 compilerVS17:languagec++11 compilerVS15:languagec++14 -0.038582437 -0.183708714 compilerVS17:languagec++14 compilerVS15:languagec++17 -0.164031495 NA compilerVS17:languagec++17 compilerVS15:languagec++20 -0.181591418 NA compilerVS17:languagec++20 compilerVS15:languagec++98 -0.193587045 0.062414667 compilerVS17:languagec++98 0.014558295 |
As an example, the (normalised) time to compile wchar.h using VS15 with languagec++11 is:
1-0.514807638-0.183862162+0.033951731-0.059720131
Each component adds/substracts to/from the normalised mean.
Building this model didn’t take long. While waiting for the kettle to boil, I suddenly realised that an additive model was probably inappropriate for this problem; oops. Surely the contribution of each component was multiplicative, i.e., components have a percentage impact to performance.
A quick change to the form of the fitted model:
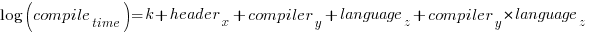
Taking the exponential of both side, the fitted equation becomes:
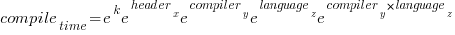
The numbers, after taking the exponent, are:
(Intercept) headerany 9.724619e+08 1.051756e+00 ... headerwctype.h headerwindows.h 3.138361e-01 2.288970e+00 compilerVS15 compilerVS17 7.286951e-01 7.772886e-01 languagec++11 languagec++14 1.011743e+00 1.049049e+00 languagec++17 languagec++20 1.067557e+00 1.056677e+00 languagec++98 compilerVS15:languagec++11 1.003249e+00 9.735327e-01 compilerVS17:languagec++11 compilerVS15:languagec++14 9.880285e-01 9.351416e-01 compilerVS17:languagec++14 compilerVS15:languagec++17 9.501834e-01 NA compilerVS17:languagec++17 compilerVS15:languagec++20 9.480678e-01 NA compilerVS17:languagec++20 compilerVS15:languagec++98 9.402461e-01 1.058305e+00 compilerVS17:languagec++98 1.001267e+00 |
Taking the same example as above: wchar.h using VS15 with c++11. The compile-time (in cpu clock cycles) is:
9.724619e+08*3.138361e-01*7.286951e-01*1.011743e+00*9.735327e-01
Now each component causes a percentage change in the (mean) base value.
Both of these model explain over 90% of the variance in the data, but this is hardly surprising given they include so much detail.
In reality compile-time is driven by some combination of additive and multiplicative factors. Building a combined additive and multiplicative model is going to be like wrestling an octopus, and is left as an exercise for the reader 🙂
Given a choice between these two models, I think the multiplicative model is probably closest to reality.
Recent Comments