Archive
Signaling cognitive firepower as a software developer
Female Peacock mate selection is driven by the number of ‘eyes’ in the tail of the available males; the more the better. Supporting a large fancy tail is biologically expensive for the male and so tail quality is a reliable signal of reproductive fitness.
A university degree used to be a reliable signal of the cognitive firepower of its owner, a quality of interest to employers looking to fill jobs that required such firepower.
Some time ago, the UK government expressed the desire for 50% of the population to attend university (when I went to university the figure was around 5%). These days, a university degree is a signal of being desperate for a job to start paying off a large debt and having an IQ in the top 50% of the population. Dumbing down is the elephant in the room.
The idea behind shifting the payment of tuition fees from the state to the student, was that as paying customers students would somehow actively ensure that universities taught stuff that was useful for getting a job. In my day, lecturers laughed when students asked them about the relevance of the material being taught to working in industry; those that persisted had their motives for attending university questioned. I’m not sure that the material taught these days is any more relevant to industry than it was in my day, but students don’t get laughed at (at least not to their face) and there is more engagement.
What could universities teach that is useful in industry? For some subjects the possible subject matter can at least be delineated (e.g., becoming a doctor), while for others a good knowledge of what is currently known about how the universe works and a familiarity with some of the maths involved is the most that can sensibly be covered in three years (when the final job of the student is unknown).
Software development related jobs often prize knowledge of the application domain above knowledge that might be learned on a computing degree, e.g., accounting knowledge when developing software for accounting systems, chemistry knowledge when working on chemical engineering software, and so on. Employers don’t want to employ people who are going to spend all their time working on the kind of issues their computing lecturers have taught them to be concerned about.
Despite the hype, computing does not appear to be as popular as other STEM subjects. I don’t see this as a problem.
With universities falling over themselves to award computing degrees to anybody who can pay and is willing to sit around for three years, how can employers separate the wheat from the chaff?
Asking a potential employee to solve a simple coding problem is a remarkably effective filter. By simple, I mean something that can be coded in 10 lines or so (e.g., read in two numbers and print their sum). There is no need to require any knowledge of fancy algorithms, the wheat/chaff division is very sharp.
The secret is to ask them to solve the problem in their head and then speak the code (or, more often than not, say it as the solution is coded in their head, with the usual edits, etc).
Burger flippers with STEM degrees
There continues to be a lot of fuss over the shortage of STEM staff (Science, technology, engineering, and mathematics). But analysis of the employment data suggests there is no STEM shortage.
One figure than jumps out is the unemployment rate for computing graduates, why is this rate of so consistently much higher than other STEM graduates, 12% vs. under 9% for the rest?
Based on my somewhat limited experience of sitting on industrial panels in university IT departments (the intended purpose of such panels is to provide industry input, but in practice we are there to rubber stamp what the department has already decided to do) and talking with recent graduates, I would explain the situation described above was follows:
The dynamics from the suppliers’ side (i.e., the Universities) is that students want a STEM degree, students are the customer (i.e., they are paying) and so the university had better provide degrees that the customer can pass (e.g., minimise the maths content and make having to learn how to program optional on computing courses). Students get a STEM degree, but those taking the ‘easy’ route are unemployable in STEM jobs.
There is not a shortage of people with STEM degrees, but there is a shortage of people with STEM degrees who can walk the talk.
Today’s burger flippers have STEM degrees that did not require students to do any serious maths or learn to program.
Evidence for 28 possible compilers in 1957
In two earlier posts I discussed the early compilers for languages that are still widely used today and a report from 1963 showing how nothing has changed in programming languages
The Handbook of Automation Computation and Control Volume 2, published in 1959, contains some interesting information. In particular Table 23 (below) is a list of “Automatic Coding Systems” (containing over 110 systems from 1957, or which 54 have a cross in the compiler column):
Computer System Name or Developed by Code M.L. Assem Inter Comp Oper-Date Indexing Fl-Pt Symb. Algeb.
Acronym
IBM 704 AFAC Allison G.M. C X Sep 57 M2 M 2 X
CAGE General Electric X X Nov 55 M2 M 2
FORC Redstone Arsenal X Jun 57 M2 M 2 X
FORTRAN IBM R X Jan 57 M2 M 2 X
NYAP IBM X Jan 56 M2 M 2
PACT IA Pact Group X Jan 57 M2 M 1
REG-SYMBOLIC Los Alamos X Nov 55 M2 M 1
SAP United Aircraft R X Apr 56 M2 M 2
NYDPP Servo Bur. Corp. X Sep 57 M2 M 2
KOMPILER3 UCRL Livermore X Mar 58 M2 M 2 X
IBM 701 ACOM Allison G.M. C X Dec 54 S1 S 0
BACAIC Boeing Seattle A X X Jul 55 S 1 X
BAP UC Berkeley X X May 57 2
DOUGLAS Douglas SM X May 53 S 1
DUAL Los Alamos X X Mar 53 S 1
607 Los Alamos X Sep 53 1
FLOP Lockheed Calif. X X X Mar 53 S 1
JCS 13 Rand Corp. X Dec 53 1
KOMPILER 2 UCRL Livermore X Oct 55 S2 1 X
NAA ASSEMBLY N. Am. Aviation X
PACT I Pact Groupb R X Jun 55 S2 1
QUEASY NOTS Inyokern X Jan 55 S
QUICK Douglas ES X Jun 53 S 0
SHACO Los Alamos X Apr 53 S 1
SO 2 IBM X Apr 53 1
SPEEDCODING IBM R X X Apr 53 S1 S 1
IBM 705-1, 2 ACOM Allison G.M. C X Apr 57 S1 0
AUTOCODER IBM R X X X Dec 56 S 2
ELI Equitable Life C X May 57 S1 0
FAIR Eastman Kodak X Jan 57 S 0
PRINT I IBM R X X X Oct 56 82 S 2
SYMB. ASSEM. IBM X Jan 56 S 1
SOHIO Std. Oil of Ohio X X X May 56 S1 S 1
FORTRAN IBM-Guide A X Nov 58 S2 S 2 X
IT Std. Oil of Ohio C X S2 S 1 X
AFAC Allison G.M. C X S2 S 2 X
IBM 705-3 FORTRAN IBM-Guide A X Dec 58 M2 M 2 X
AUTOCODER IBM A X X Sep 58 S 2
IBM 702 AUTOCODER IBM X X X Apr 55 S 1
ASSEMBLY IBM X Jun 54 1
SCRIPT G. E. Hanford R X X X X Jul 55 Sl S 1
IBM 709 FORTRAN IBM A X Jan 59 M2 M 2 X
SCAT IBM-Share R X X Nov 58 M2 M 2
IBM 650 ADES II Naval Ord. Lab X Feb 56 S2 S 1 X
BACAIC Boeing Seattle C X X X Aug 56 S 1 X
BALITAC M.I.T. X X X Jan 56 Sl 2
BELL L1 Bell Tel. Labs X X Aug 55 Sl S 0
BELL L2,L3 Bell Tel. Labs X X Sep 55 Sl S 0
DRUCO I IBM X Sep 54 S 0
EASE II Allison G.M. X X Sep 56 S2 S 2
ELI Equitable Life C X May 57 Sl 0
ESCAPE Curtiss-Wright X X X Jan 57 Sl S 2
FLAIR Lockheed MSD, Ga. X X Feb 55 Sl S 0
FOR TRANSIT IBM-Carnegie Tech. A X Oct 57 S2 S 2 X
IT Carnegie Tech. C X Feb 57 S2 S 1 X
MITILAC M.I.T. X X Jul 55 Sl S 2
OMNICODE G. E. Hanford X X Dec 56 Sl S 2
RELATIVE Allison G.M. X Aug 55 Sl S 1
SIR IBM X May 56 S 2
SOAP I IBM X Nov 55 2
SOAP II IBM R X Nov 56 M M 2
SPEED CODING Redstone Arsenal X X Sep 55 Sl S 0
SPUR Boeing Wichita X X X Aug 56 M S 1
FORTRAN (650T) IBM A X Jan 59 M2 M 2
Sperry Rand 1103A COMPILER I Boeing Seattle X X May 57 S 1 X
FAP Lockheed MSD X X Oct 56 Sl S 0
MISHAP Lockheed MSD X Oct 56 M1 S 1
RAWOOP-SNAP Ramo-Wooldridge X X Jun 57 M1 M 1
TRANS-USE Holloman A.F.B. X Nov 56 M1 S 2
USE Ramo-Wooldridge R X X Feb 57 M1 M 2
IT Carn. Tech.-R-W C X Dec 57 S2 S 1 X
UNICODE R Rand St. Paul R X Jan 59 S2 M 2 X
Sperry Rand 1103 CHIP Wright A.D.C. X X Feb 56 S1 S 0
FLIP/SPUR Convair San Diego X X Jun 55 SI S 0
RAWOOP Ramo-Wooldridge R X Mar 55 S1 1
8NAP Ramo-Wooldridge R X X Aug 55 S1 S 1
Sperry Rand Univac I and II AO Remington Rand X X X May 52 S1 S 1
Al Remington Rand X X X Jan 53 S1 S 1
A2 Remington Rand X X X Aug 53 S1 S 1
A3,ARITHMATIC Remington Rand C X X X Apr 56 SI S 1
AT3,MATHMATIC Remington Rand C X X Jun 56 SI S 2 X
BO,FLOWMATIC Remington Rand A X X X Dec 56 S2 S 2
BIOR Remington Rand X X X Apr 55 1
GP Remington Rand R X X X Jan 57 S2 S 1
MJS (UNIVAC I) UCRL Livermore X X Jun 56 1
NYU,OMNIFAX New York Univ. X Feb 54 S 1
RELCODE Remington Rand X X Apr 56 1
SHORT CODE Remington Rand X X Feb 51 S 1
X-I Remington Rand C X X Jan 56 1
IT Case Institute C X S2 S 1 X
MATRIX MATH Franklin Inst. X Jan 58
Sperry Rand File Compo ABC R Rand St. Paul Jun 58
Sperry Rand Larc K5 UCRL Livermore X X M2 M 2 X
SAIL UCRL Livermore X M2 M 2
Burroughs Datatron 201, 205 DATACODEI Burroughs X Aug 57 MS1 S 1
DUMBO Babcock and Wilcox X X
IT Purdue Univ. A X Jul 57 S2 S 1 X
SAC Electrodata X X Aug 56 M 1
UGLIAC United Gas Corp. X Dec 56 S 0
Dow Chemical X
STAR Electrodata X
Burroughs UDEC III UDECIN-I Burroughs X 57 M/S S 1
UDECOM-3 Burroughs X 57 M S 1
M.I.T. Whirlwind ALGEBRAIC M.I.T. R X S2 S 1 X
COMPREHENSIVE M.I.T. X X X Nov 52 Sl S 1
SUMMER SESSION M.I.T. X Jun 53 Sl S 1
Midac EASIAC Univ. of Michigan X X Aug 54 SI S
MAGIC Univ. of Michigan X X X Jan 54 Sl S
Datamatic ABC I Datamatic Corp. X
Ferranti TRANSCODE Univ. of Toronto R X X X Aug 54 M1 S
Illiac DEC INPUT Univ. of Illinois R X Sep 52 SI S
Johnniac EASY FOX Rand Corp. R X Oct 55 S
Norc NORC COMPILER Naval Ord. Lab X X Aug 55 M2 M
Seac BASE 00 Natl. Bur. Stds. X X
UNIV. CODE Moore School X Apr 55 |
Chart Symbols used:
Code R = Recommended for this computer, sometimes only for heavy usage. C = Common language for more than one computer. A = System is both recommended and has common language. Indexing M = Actual Index registers or B boxes in machine hardware. S = Index registers simulated in synthetic language of system. 1 = Limited form of indexing, either stopped undirectionally or by one word only, or having certain registers applicable to only certain variables, or not compound (by combination of contents of registers). 2 = General form, any variable may be indexed by anyone or combination of registers which may be freely incremented or decremented by any amount. Floating point M = Inherent in machine hardware. S = Simulated in language. Symbolism 0 = None. 1 = Limited, either regional, relative or exactly computable. 2 = Fully descriptive English word or symbol combination which is descriptive of the variable or the assigned storage. Algebraic A single continuous algebraic formula statement may be made. Processor has mechanisms for applying associative and commutative laws to form operative program. M.L. = Machine language. Assem. = Assemblers. Inter. = Interpreters. Compl. = Compilers. |
Are the compilers really compilers as we know them today, or is this terminology that has not yet settled down? The computer terminology chapter refers readers interested in Assembler, Compiler and Interpreter to the entry for Routine:
“Routine. A set of instructions arranged in proper sequence to cause a computer to perform a desired operation or series of operations, such as the solution of a mathematical problem.
…
Compiler (compiling routine), an executive routine which, before the desired computation is started, translates a program expressed in pseudo-code into machine code (or into another pseudo-code for further translation by an interpreter).
…
Assemble, to integrate the subroutines (supplied, selected, or generated) into the main routine, i.e., to adapt, to specialize to the task at hand by means of preset parameters; to orient, to change relative and symbolic addresses to absolute form; to incorporate, to place in storage.
…
Interpreter (interpretive routine), an executive routine which, as the computation progresses, translates a stored program expressed in some machine-like pseudo-code into machine code and performs the indicated operations, by means of subroutines, as they are translated. …”
The definition of “Assemble” sounds more like a link-load than an assembler.
When the coding system has a cross in both the assembler and compiler column, I suspect we are dealing with what would be called an assembler today. There are 28 crosses in the Compiler column that do not have a corresponding entry in the assembler column; does this mean there were 28 compilers in existence in 1957? I can imagine many of the languages being very simple (the fashionability of creating programming languages was already being called out in 1963), so producing a compiler for them would be feasible.
The citation given for Table 23 contains a few typos. I think the correct reference is: Bemer, Robert W. “The Status of Automatic Programming for Scientific Problems.” Proceedings of the Fourth Annual Computer Applications Symposium, 107-117. Armour Research Foundation, Illinois Institute of Technology, Oct. 24-25, 1957.
Programming Languages: nothing changes
While rummaging around today I came across: Programming Languages and Standardization in Command and Control by J. P. Haverty and R. L. Patrick.
Much of this report could have been written in 2013, but it was actually written fifty years earlier; the date is given away by “… the effort to develop programming languages to increase programmer productivity is barely eight years old.”
Much of the sound and fury over programming languages is the result of zealous proponents touting them as the solution to the “programming problem.”
I don’t think any major new sources of sound and fury have come to the fore.
… the designing of programming languages became fashionable.
Has it ever gone out of fashion?
Now the proliferation of languages increased rapidly as almost every user who developed a minor variant on one of the early languages rushed into publication, with the resultant sharp increase in acronyms. In addition, some languages were designed practically in vacuo. They did not grow out of the needs of a particular user, but were designed as someone’s “best guess” as to what the user needed (in some cases they appeared to be designed for the sake of designing).
My post on this subject was written 49 years later.
…a computer user, who has invested a million dollars in programming, is shocked to find himself almost trapped to stay with the same computer or transistorized computer of the same logical design as his old one because his problem has been written in the language of that computer, then patched and repatched, while his personnel has changed in such a way that nobody on his staff can say precisely what the data processing Job is that his machine is now doing with sufficient clarity to make it easy to rewrite the application in the language of another machine.
Vendor lock-in has always been good for business.
Perhaps the most flagrantly overstated claim made for POLs is that they result in better understanding of the programming operation by higher-level management.
I don’t think I have ever heard this claim made. But then my programming experience started a bit later than this report.
… many applications do not require the services of an expert programmer.
Ssshh! Such talk is bad for business.
The cost of producing a modern compiler, checking it out, documenting it, and seeing it through initial field use, easily exceeds $500,000.
For ‘big-company’ written compilers this number has not changed much over the years. Of course man+dog written compilers are a lot cheaper and new companies looking to aggressively enter the market can spend an order of magnitude more.
In a young rapidly growing field major advances come so quickly or are so obvious that instituting a measurement program is probably a waste of time.
True.
At some point, however, as a field matures, the costs of a major advance become significant.
Hopefully this point in time has now arrived.
Language design is still as much an art as it is a science. The evaluation of programming languages is therefore much akin to art criticism–and as questionable.
Calling such a vanity driven activity an ‘art’ only helps glorify it.
Programming languages represent an attack on the “programming problem,” but only on a portion of it–and not a very substantial portion.
In fact, it is probably very insubstantial.
Much of the “programming problem” centers on the lack of well-trained experienced people–a lack not overcome by the use of a POL.
Nothing changes.
The following table is for those of you complaining about how long it takes to compile code these days. I once had to compile some Coral 66 on an Elliot 903, the compiler resided in 5(?) boxes of paper tape, one box per compiler pass. Compilation involved: reading the paper tape containing the first pass into the computer, running this program and then reading the paper tape containing the program source, then reading the second paper tape containing the next compiler pass (there was not enough memory to store all compiler passes at once), which processed the in-memory output of the first pass; this process was repeated for each successive pass, producing a paper tape output of the compiled code. I suspect that compiling on the machines listed gave the programmers involved plenty of exercise and practice splicing snapped paper-tape.
Computer Cobol statements Machine instructions Compile time (mins) UNIVAC II 630 1,950 240 RCA 501 410 2,132 72 GE 225 328 4,300 16 IBM 1410 174 968 46 NCR 304 453 804 40 |
What is empirical software engineering?
Writing a book about empirical software engineering requires making decisions about which subjects to discuss and what to say about them.
The obvious answer to “which subjects” is to include everything that practicing software engineers do, when working on software systems; there are some obvious exclusions like traveling to work. To answer the question of what software engineers do, I have relied on personal experience, my own and what others have told me. Not ideal, but it’s the only source of information available to me.
The foundation of an empirical book is data, and I only talk about subjects for which public data is available. The data requirement is what makes writing this book practical; there is not a lot of data out there. This lack of data has allowed me to avoid answering some tricky questions about whether something is, or is not, part of software engineering.
What approach should be taken to discussing the various subjects? Economics, as in cost/benefit analysis, is the obvious answer.
In my case, I am a developer and the target audience is developers, so the economic perspective is from the vendor side, not the customer side (e.g., maximizing profit, not minimizing cost or faults). Most other books have a customer oriented focus, e.g., high reliability is important (with barely a mention of the costs involved); this focus on a customer oriented approach comes from the early days of computing where the US Department of Defense funded a lot of software research driven by their needs as a customer.
Again the lack of data curtails any in depth analysis of the economic issues involved in software development. The data is like a patchwork of islands, the connections between them are under water and have to be guessed at.
Yes, I am writing a book on empirical software engineering that contains the sketchiest of outlines on what empirical software engineering is all about. But if the necessary data was available, I would not live long enough to get close to completing the book.
What of the academic take on empirical software engineering? Unfortunately the academic incentive structure strongly biases against doing work of interest to industry; some of the younger generation do address industry problems, but they eventually leave or get absorbed into the system. Academics who spend time talking to people in industry, to find out what problems exist, tend to get offered jobs in industry; university managers don’t like loosing their good people and are incentivized to discourage junior staff fraternizing with industry. Writing software is not a productive way of generating papers (academics are judged by the number and community assessed quality of papers they produce), so academics spend most of their work time babbling in front of spotty teenagers; the result is some strange ideas about what industry might find useful.
Academic software engineering exists in its own self-supporting bubble. The monkeys type enough papers that it is always possible to find some connection between an industry problem and published ‘research’.
Warp your data to make it visually appealing
Data plots can sometimes look very dull and need to be jazzed up a bit. Now, nobody’s suggesting that the important statistical properties of the data be changed, but wouldn’t it be useful if the points could be moved around a bit, to create something visually appealing without losing the desired statistical properties?
Readers have to agree that the plot below looks like fun. Don’t you wish your data could be made to look like this?
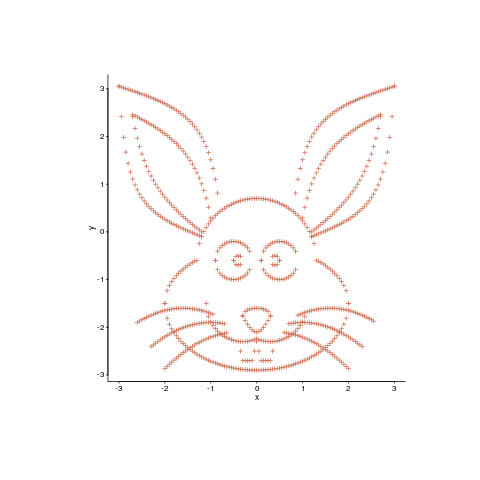
Well, now you can (code here, inspired by Matejka and Fitzmaurice who have not released their code yet). It is also possible to thin-out the points, while maintaining the visual form of the original image.
The idea is to perturb the x/y position of very point by a small amount, such that the desired statistical properties are maintained to some level of accuracy:
check_prop=function(new_pts, is_x)
{
if (is_x)
return(abs(myx_mean-stat_cond(new_pts)) < 0.01)
else
return(abs(myy_mean-stat_cond(new_pts)) < 0.01)
}
mv_pts=function(pts)
{
repeat
{
new_x=pts$x+runif(num_pts, -0.01, 0.01)
if (check_prop(new_x, TRUE))
break()
}
repeat
{
new_y=pts$y+runif(num_pts, -0.01, 0.01)
if (check_prop(new_y, FALSE))
break()
}
return(data.frame(x=new_x, y=new_y))
} |
The distance between the perturbed points and the positions of the target points then needs to be calculated. For each perturbed point its nearest neighbor in the target needs to be found and the distance calculated. This can be done in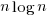 
using kd-trees and of course there is an R package, RANN, do to this (implemented in the nn2 function). The following code tries to minimize the sum of the distances, another approach is to minimize the mean distance:
mv_closer=function(pts)
{
repeat
{
new_pts=mv_pts(pts)
new_dist=nn2(rabbit, new_pts, k=1)
if (sum(new_dist$nn.dists) < cur_dist)
{
cur_dist <<- sum(new_dist$nn.dists)
return(new_pts)
}
}
} |
Now it’s just a matter of iterating lots of times, existing if the distance falls below some limit:
iter_closer=function(tgt_pts, src_pts)
{
cur_dist <<- sum(nn2(tgt_pts, src_pts, k=1)$nn.dists)
cur_pts=src_pts
for (i in 1:5000)
{
new_pts=mv_closer(cur_pts)
cur_pts=new_pts
if (cur_dist < 13)
return(cur_pts)
}
return(cur_pts)
} |
This code handles a single statistical property. Matejka and Fitzmaurice spent more than an hour on their implementation, handle multiple properties and use simulated annealing to prevent being trapped in local minima.
An example, with original points in yellow:
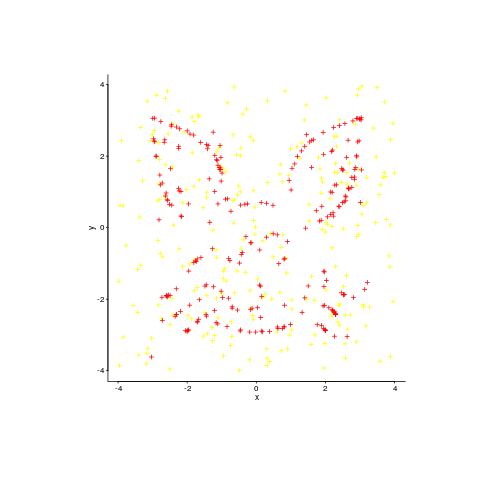
Enjoy.
Recent Comments