Archive
The wind is not yet blowing in software engineering research
An article by Andrew Gelman is getting a lot of well deserved publicity at the moment. The topic of discussion is sloppy research practices in psychology and how researchers are responding to criticism (head in the sand and blame the messenger).
I imagine that most software developers think this is an intrinsic problem in the ‘soft’ sciences that does not apply to the ‘hard’ sciences, such as software; I certainly thought this until around 2000 or so. Writing a book containing a detailed analysis of C convinced me that software engineering was mostly opinion, with a tiny smattering of knowledge in places.
The C book tried to apply results from cognitive psychology to what software developers do. After reading lots of books and papers on cognitive psychology I was impressed with how much more advanced, and rigorous, their experimental methods were, compared to software engineering.
Writing a book on empirical software engineering has moved my views on to the point where I think software engineering is the ideal topic for the academic fraudster.
The process of cleaning up their act that researchers in psychology are going through now is something that software engineering will have to go through. Researchers have not yet reached the stage of directly pointing out that software engineering research is a train wreck. Instead, they write parody papers and polite article showing how dirty popular datasets are.
Of course, industry is happy to keep quiet. The development of software systems is still a sellers market (the packaged market is dog eat dog) or at least that is still the prevalent mentality. I doubt anything much will change until the production of software systems becomes a buyers market, which will create a real incentive for finding out what really works.
Converting between IFPUG & COSMIC function point counts
Replication, repeating an experiment to confirm the results of previous experiments, is not a common activity in software engineering. Everybody wants to write about their own ideas and academic journals want to publish what is new (they are fashion driven).
Conversion between ways of counting function points, a software effort estimating technique, is one area where there has been a lot of replications (eight studies is a lot in software engineering, while a couple of hundred is a lot in psychology).
Amiri and Padmanabhuni’s Master’s thesis (yes, a thesis written by two people) lists data from 11 experiments where students/academics/professionals counted function points for a variety of projects using both the IFPUG and COSMIC counting methods. The data points are plotted below left and regression lines to each sample on the right (code+data):
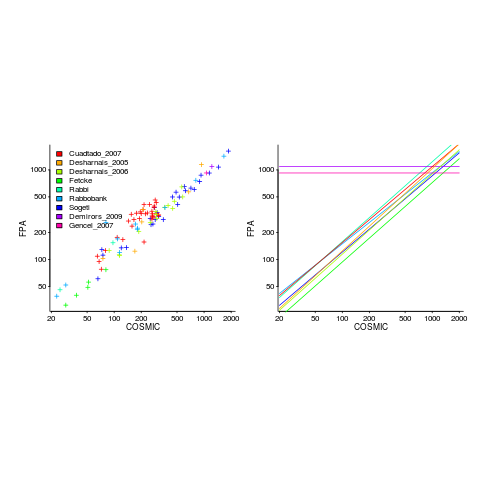
The horizontal lines are two very small samples where model fitting failed.
I was surprised to see such good agreement between different groups of counters. A study by Grimstad and Jørgensen asked developers to estimate effort (not using function points) for various projects, waited one month and repeated using what the developers thought were different projects. Most of the projects were different from the first batch, but a few were the same. The results showed developers giving completely different estimates for the same project! It looks like the effort invested in producing function point counting rules that give consistent answers and the training given to counters has paid off.
Two patterns are present in the regression lines:
- the slope of most lines is very similar, but they are offset from each other,
- the slope of some lines is obviously different from the others, with the different slopes all tilting further in the same direction. These cases mostly occur in the Cuadrado data (these three data sets are not included in the following analysis).
The kind of people doing the counting, for each set of measurements, is known and this information can be used to build a more sophisticated model.
Specifying a regression model to fit requires making several decisions about the kinds of uncertainty error present in the data. I have no experience with function points and in the following analysis I list the options and pick the one that looks reasonable to me. Please let me know if you have theory or data one suggesting what the right answer might be, I’m just juggling numbers here.
First we have to decide whether measurement error is additive or multiplicative. In other words, is there a fixed amount of potential error on each measurement, or is the amount of error proportional to the size of the project being measured (i.e., the error is a percentage of the total).
Does it make a difference to the fitted model? Sometimes it does and its always worthwhile to try building a model that mimics reality. If I tell you that 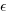 (Greek lower-case epsilon) is the symbol used to denote measurement error, you should be able to figure out which of the following two equations was built assuming additive/multiplicative error (confidence intervals have been omitted to keep things simple, they are given at the end of this post).
(Greek lower-case epsilon) is the symbol used to denote measurement error, you should be able to figure out which of the following two equations was built assuming additive/multiplicative error (confidence intervals have been omitted to keep things simple, they are given at the end of this post).
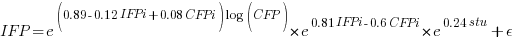
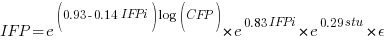
where: 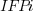 is 0 when the IFPUG counting is done by academics and 1 when done by industry,
is 0 when the IFPUG counting is done by academics and 1 when done by industry, 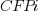 is 0 when the COSMIC counting is done by academics and 1 when done by industry,
is 0 when the COSMIC counting is done by academics and 1 when done by industry, 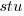 is 1 when the counting was done by students and 0 otherwise.
is 1 when the counting was done by students and 0 otherwise.
I think that measurement error is multiplicative for his problem and the remaining discussion is based on this assumption. Everything after the first exponential can be treated as effectively a constant, say  , giving:
, giving:
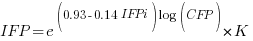
If we are only interested in converting counts performed by industry we get:
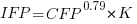
If we are using academic counters the equation is:

Next we have to decide where the uncertainty error resides. Nearly all forms of regression modeling assume that all the uncertainty resides in the response variable and that there is no uncertainty in the explanatory variables are measured without uncertainty. The idea is that the values of the explanatory variables are selected by the person doing the measurement, a handle gets turned and out pops the value of the response variable, plus error, for those particular, known, explanatory variable.
The measurements in this analysis were obtained by giving the subjects a known project specification, getting them to turn a handle and recording the function point count that popped out. So all function point counts contain uncertainty error.
Does the choice of response variable make that big a difference?
Let’s take the model fitted above and do some algebra to invert it, so that COSMIC is expressed in terms of IFPUG. We get the equation:
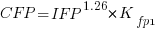
Now lets fit a model where the roles of response/explanatory variable are switched, we get:
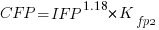
For this problem we need to fit a model that includes uncertainty in both variables containing function point counts. There are techniques for building models from scratch, known as errors-in-variables models. I like the SIMEX approach because it integrates well with existing R functionality for building regression models.
To use the simex function, from the R simex package, I have to decide how much uncertainty (in the form of a value for standard deviation) is present in the explanatory variable (the COSMIC counts in this case). Without any knowledge to guide the choice, I decided that the amount of error in both sets of count measurements is the same (a standard deviation of 3%, please let me know if you have a better idea).
The fitted equation for a model containing uncertainty in both counts is (see code+data for model details):
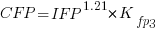
If I am interested in converting IFPUG counts to COSMIC, then what is the connection between the above model and reality?
I’m guessing that those most likely to perform conversions are in industry. Does this mean we can delete the academic subexpressions from the model, or perhaps fit a model that excludes counts made by academics? Is the Cuadrado data sufficiently different to be treated as an outlier than should be excluded from the model building process, or is it representative of an industry usage that does not occur in the available data?
There are not many industry only counts in the combined data. Perhaps the academic counters are representative of counters in industry that happen not to be included in the samples. We could build a mixed-effects model, using all the data, to get some idea of the variation between different sets of counters.
The 95% confidence intervals for the fitted exponent coefficient, using this data, is around 8%. So in practice, some of the subtitles in the above analysis are lost in the noise. To get tighter confidence bounds more data is needed.
p-values in software engineering
Data relating to software engineering activities is starting to become common and the results of any statistical analysis of data will include something known as the p-value.
Most of the time having a p-value below some cut-off value is a good thing, but sometimes good things occur when the value is above the cut-off (see p-values for programmers for details about what the p-value is).
A commonly encountered cut-off value is 0.05 (sometimes written as 5%).
Where did this 0.05 come from? It was first proposed in 1920s by Ronald Fisher. Fisher’s Statistical Methods for Research Workers and later Statistical Tables for Biological, Agricultural, and Medical Research had a huge impact and a p-value cut-off of 0.05 became enshrined as the magic number.
To quote Fisher: “Either there is something in the treatment, or a coincidence has occurred such as does not occur more than once in twenty trials.”
Once in twenty was a reasonable level for an event occurring by chance (rather than as a result of some new fertilizer or drug) in an experiment in biological, agricultural or medical research in 1900s. Is it a reasonable level for chance events in software engineering?
A one in twenty chance of a new technique resulting in a building falling down would not be considered acceptable in civil engineering. In high energy physics a p-value of 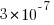 is used to decide whether a new particle has been discovered (or not).
is used to decide whether a new particle has been discovered (or not).
In business p-values should be treated as part of cost/benefit analysis. How confident are we that this effect is for real, how much would it cost to be right or wrong about it? Using a cut-off value to make yes/no decisions (e.g., 0.049 yes, 0.051 no) is very simplistic decision making.
To get a paper published in a software engineering journal requires any data analysis to have p-values below 0.05. In this regard the editors are aping journals in the social sciences; in fact the high impact social science journals require p-values below 0.01 (the high impact journals receive more submissions and can afford to be choosier about what they publish).
What is a sensible choice for a p-value cur-off in software engineering journals? The simple answer is: As low as possible, given the need to accept  papers per month for publication. A more complicated answer would involve different cut-offs for different kinds of measurements, e.g., measuring people or measuring code.
papers per month for publication. A more complicated answer would involve different cut-offs for different kinds of measurements, e.g., measuring people or measuring code.
While the p-value attracts plenty of criticism, there is nothing wrong with p-values. Use of p-values has a dominant market position in statistics and they are frequently misused by the clueless and those wanting to mislead their audience. Any other technique is just as likely to be misused, if not more so.
The killer phrase associated with p-values is “statistically significant”, often abbreviated to just “significant”. How people love to describe the results of their measurements as being shown to be “significant”. Of course, I am free to choose whatever p-value cut-off I like for my experiments and then claim the results are significant. I have had researchers repeatedly tell me that their results were “significant”, every time I asked them about p-values; a serious red flag.
When dealing with statistical results, ask yourself what the reported p-values mean to you. Don’t accept the 0.05 is the cut-off that everybody uses nonsense. If the research won’t reveal actual p-values, walk away from the snake oil.
Software engineering data sets
The pretty pictures from my empirical software engineering book are now online, along with the 210 data sets and R code (330M).
Plotting the number of data sets in each year shows that empirical software engineering has really taken off in the last 10 years (code+data). Around dozen or so confidential data sets are not included; I am only writing about data that can be made public.
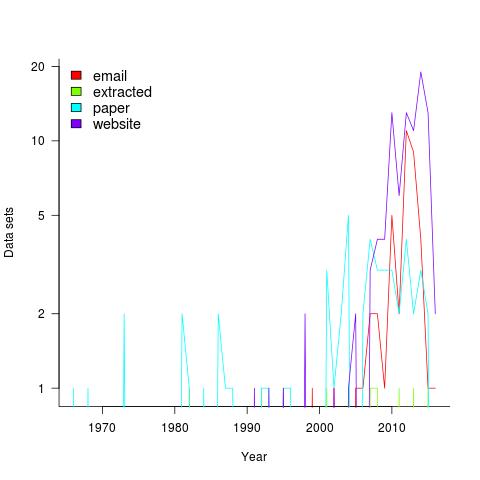
It used to be rare to find the data associated with a paper on the author’s website. Of course, before around 1995 there was no web, but since around 2012 the idea has started to take off.
Contact via email goes back to 1985 and before that people sent mag tapes through the post and many years ago somebody sent me punched tape (there is nothing like seeing the bits with the naked eye).
I have sent several hundred emails asking for data and received 55 data sets. I’m hoping this release will spur those who have promised me data to invest some time to send it.
My experience is that research data often lives on laptops and dies when the laptop is replaced (a study of biologists, who have been collecting data for hundreds of years, found a data ‘death rate’ of 17% a year). Had I started actively collecting data before 2010 the red line in the plot would be much higher for earlier years; I often received data from authors when writing my C book at the start of the century (Google went from nothing to being the best place to search, while I wrote).
In nine cases I extracted the data, either from the pdf or an image and then reverse engineered values.
I have around 50 data sets waiting to be processed. Given that lots more are bound to arrive before the book is finished, I expect to easily reach the 300 mark. A tiny number given my aim of writing about all software engineering issues for which public data exists.
If you know of interesting software engineering data, that is not to be found in these plots, please let me know.
Recent Comments