Preferential attachment applied to frequency of accessing a variable
If, when writing code for a function, up to the current point in the code 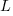 distinct local variables have been accessed for reading
distinct local variables have been accessed for reading 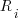 times (
times (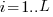 ), will the next read access be from a previously unread local variable and if not what is the likelihood of choosing each of the distinct
), will the next read access be from a previously unread local variable and if not what is the likelihood of choosing each of the distinct 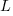 variables (global variables are ignored in this analysis)?
variables (global variables are ignored in this analysis)?
Short answer:
- With probability
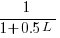 select a new variable to access,
select a new variable to access, - otherwise select a variable that has previously been accessed in the function, with the probability of selecting a particular variable being proportional to
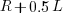 (where
(where 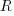 is the number of times the variable has previously been read from.
is the number of times the variable has previously been read from.
The longer answer is below as another draft section from my book Empirical software engineering with R. As always comments and pointers to more data welcome. R code and data here.
The discussion on preferential attachment is embedded in a discussion of model building.
What kind of model to build?
The obvious answer to the question of what kind of model to build is, the cheapest one that produces the desired output.
Many of the model building techniques discussed in this book find patterns in the data and effectively return one or more equations that produce output similar to the data given some set of inputs; the equations are the model.
The advantage of this approach is that in many cases the implementation of the model building has been automated (I don’t say much about those that have not yet been automated), the user contribution is in choosing which kind of model to build. In some cases the R function requires that the user provide a general direction of attack (e.g., the form of function to use in fitting a nonlinear regression).
An alternative kind of model is one whose output is obtained by running an iterative algorithm, e.g., a time series created by calculating the next value in a sequence from one or more previous values.
In most cases a great deal of domain knowledge is required of the user building the model, while in a few cases an automated procedure for creating the iterative algorithm and its parameters is available, e.g., time series analysis.
There is never any guarantee that any created model will be sufficiently accurate to be useful for the problem at hand; this is a risk that occurs in all model building exercises.
The following discussion builds two models, one using an established automated model building technique (regression) and the other using an iterative algorithm built using domain knowledge coupled with experimentation.
The problem
Consider local variable usage within a function. If a function contains a total of  read accesses to locally defined variables, how many variables will be read from only once, how many twice and so on (this is a static count extracted from the source code, not a dynamic count obtained by executing the function)?
read accesses to locally defined variables, how many variables will be read from only once, how many twice and so on (this is a static count extracted from the source code, not a dynamic count obtained by executing the function)?
The data for the following analysis is from Jones <book Jones_05a> (see figure 1821.5) and contains three columns, total count: the total number of read accesses to all variables defined within a function definition, object access: the number of read accesses from a distinct local variable, and occurrences: the number of distinct variables that have at least one read access within the function (i.e., unused variables are not counted); the occurrences counts have been summed over all functions.
In the following extract, within functions containing 24 totals accesses there were 783 occurrences of variables accessed once, 697 occurrences of variables accessed twice and so on.
total access,object access,occurrences 24,1,783 24,2,697 24,3,474 |
The data excludes everything about source code apart from read access information.
Fitting an equation to the data
Plotting the data shows an exponential-like decrease in occurrences as the number of accesses to a variable increases (i.e., most variables are accessed a small number of time); also there is an overall increase in the counts as the total numbers of accesses increases (see below).
The fit obtained by the nls function for a simple exponential equation is the following (all p-values less than 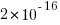 ; see rexample[local-use]):
; see rexample[local-use]):
where 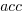 is the number of read accesses to a given variable and
is the number of read accesses to a given variable and  is the total accesses to all local variables within the function. Because the data has been normalised the value returned is a percentage.
is the total accesses to all local variables within the function. Because the data has been normalised the value returned is a percentage.
As an example, a function containing a total of 30 read accesses of local variables the expected percentage of variables accessed twice is: 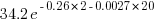 .
.
Modeling with an incremental algorithm
If, when writing code for a function, up to the current point in the code 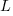 distinct local variables have been accessed for reading
distinct local variables have been accessed for reading 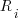 times (
times (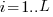 ), will the next read access be from a previously unread local variable and if not what is the likelihood of choosing each of the distinct
), will the next read access be from a previously unread local variable and if not what is the likelihood of choosing each of the distinct 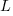 variables (global variables are ignored in this analysis)?
variables (global variables are ignored in this analysis)?
Each access in the code of a local variable could be thought of as a link to the information contained in that variable. One algorithm that has been found to do a reasonable job of modeling the number of links between web pages is Preferential attachment. Might this algorithm also be applicable to modeling read accesses to local variables?
The Preferential attachment algorithm is:
- With probability
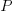 select a new web page (in this case a new variable to access),
select a new web page (in this case a new variable to access), - with probability
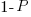 select an existing web page (a variable that has previously been accessed in the function), select a variable with a probability proportional to the number of times it has previously been accessed (i.e., a variable that has four previous read accesses is twice as likely to be chosen as one that has had two previous accesses).
select an existing web page (a variable that has previously been accessed in the function), select a variable with a probability proportional to the number of times it has previously been accessed (i.e., a variable that has four previous read accesses is twice as likely to be chosen as one that has had two previous accesses).
The following plot shows the results of running this algorithm 1,000 times each with 100 total accesses per function definition, for two values of 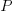 (left plot 0.05, right plot 0.0004, red points) and smoothed data (blue points; smoothing involved summing the access counts for all measured functions having total accesses between 96 and 104), green line is a fitted exponential. Values have been normalised so that variables with one access have a count of 100, also access counts greater than 20 have a very low occurrences and are not plotted.
(left plot 0.05, right plot 0.0004, red points) and smoothed data (blue points; smoothing involved summing the access counts for all measured functions having total accesses between 96 and 104), green line is a fitted exponential. Values have been normalised so that variables with one access have a count of 100, also access counts greater than 20 have a very low occurrences and are not plotted.
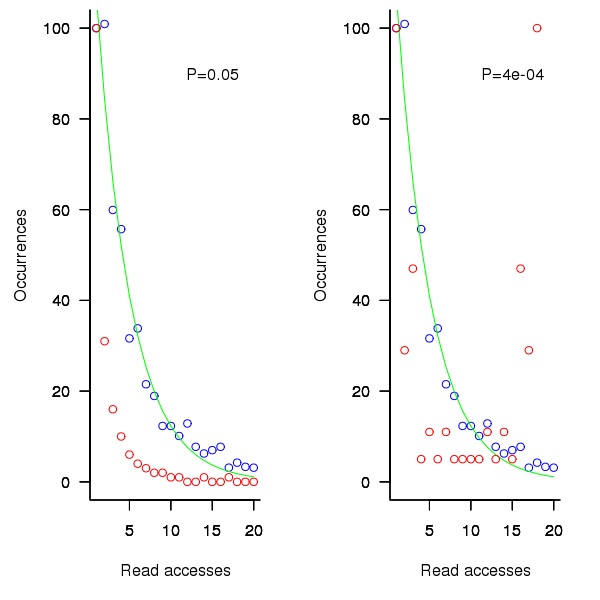
Figure 1. Variables having a given number of read accesses, given 100 total accesses, calculated from running the preferential attachment algorithm with probability of accessing a new variable at 0.05 (left, in red) and 0.0004 (right, in red), the smoothed data (blue) and a fitted exponential (green).
The results show that decreasing the probability of accessing a new variable, 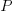 , does not shift the distribution of occurrences in the desired way. Note: the well known analytic solution to the outcome of running the preferential attachment algorithm, i.e., a power law, applies in the situation where the number of accesses per function definition goes to infinity.
, does not shift the distribution of occurrences in the desired way. Note: the well known analytic solution to the outcome of running the preferential attachment algorithm, i.e., a power law, applies in the situation where the number of accesses per function definition goes to infinity.
The Preferential attachment algorithm uses a fixed probability for deciding whether to access a new variable; other measurements <book Jones_05a> imply that in practice this probability decreases as the number of distinct local variables increases. An obvious modification is to use a probability having a form something like
the number of distinct variables accessed so far). A little experimentation finds that 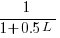 produces results that more closely mimic the data.
produces results that more closely mimic the data.
While 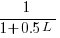 improves the fit for infrequently accessed variables, the weighting system used to select a previously accessed variable still needs attention; perhaps it also has a dependency on
improves the fit for infrequently accessed variables, the weighting system used to select a previously accessed variable still needs attention; perhaps it also has a dependency on 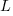 . Some experimentation finds that changing the probability of selection from
. Some experimentation finds that changing the probability of selection from 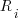 to
to 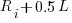 (where
(where  is the number of read accesses to variable
is the number of read accesses to variable  so far) produces behavior that matches the data to the same degree as the exponential model.
so far) produces behavior that matches the data to the same degree as the exponential model.
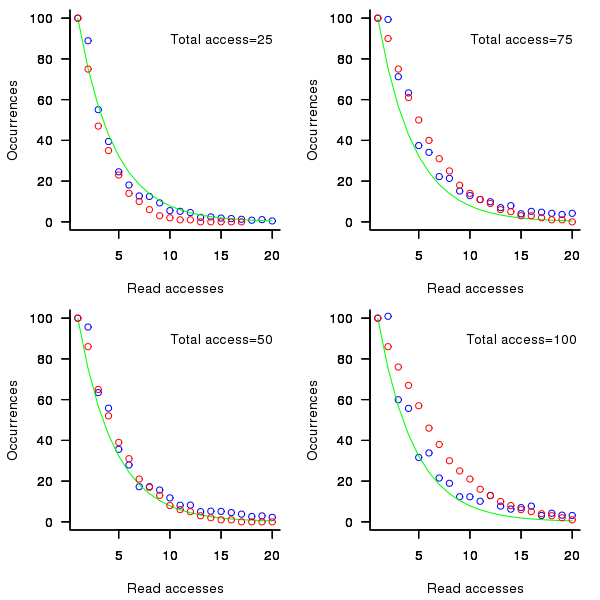
Figure 2. Variables having a given number of read accesses, given 25, 50, 75 and 100 total accesses, calculated from running the weighted preferential attachment algorithm (red), the smoothed data (blue) and a fitted exponential (green).
The weighted preferential attachment algorithm is as follows:
- With probability
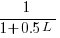 select a new variable to access,
select a new variable to access, - with probability
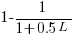 select a variable that has previously been accessed in the function, select an existing variable with probability proportional to
select a variable that has previously been accessed in the function, select an existing variable with probability proportional to 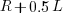 (where
(where 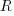 is the number of times the variable has previously been read from; e.g., if the total accesses up to this point in the code is 12, a variable that has had four previous read accesses is
is the number of times the variable has previously been read from; e.g., if the total accesses up to this point in the code is 12, a variable that has had four previous read accesses is 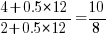 times as likely to be chosen as one that has had two previous accesses).
times as likely to be chosen as one that has had two previous accesses).
So what?
Both of the models are wrong in that they do not account for the small number of very frequently accessed variables that regularly occur in the data. However, as the adage goes: All models are wrong but some are useful; usefulness being evaluated by the extent to which a model solves the problem at hand. Both models have their own advantages and disadvantages, including:
- the fitted equation is quick and simple to calculate, while the output from the algorithmic model has to be averaged over many runs (1,000 are used in the example code) and is much slower,
- the algorithm automatically generates a possible sequence of accesses, while the equation does not provide an obvious way for generating a sequence of accesses,
- multiple executions of the algorithm can be used to obtain an estimate of standard deviation, while the equation does not provide a method for estimating this quantity (it may be possible to build another regression model that provides this information),
If insight into variable usage is the aim, each model provides its own particular kind of insight:
- the equation provides an end result way of thinking about how the number of variables having a given number of accesses changes, but does not provide any insight into the decision process at the level of individual accesses,
- the algorithm provides a way of thinking about how choices are made for each access, but does not provide any insight into the behavior of the final counts.
Other application domains and languages
The data used to build these models was extracted from the C source code of what might be termed desktop applications. Will the same variable access behavior characteristics occur in source written for other application domain or in other languages?
Variables might be broadly grouped into those used to hold application values (e.g., length of something) and those used to hold housekeeping values (e.g., loop counters).
Application variables are likely to be language invariant but have some dependence on algorithm (e.g., stored in an array or linked list) or cultural coding habits (e.g., within the embedded community accessing local variables is often considered to be much less efficient than accessing global variables and there are measurably different usage patterns <book Engblom_99a><book Jones 05a> figure 288.1).
The need for housekeeping values will depend on the construct supported by a language. For instance, in C loops often involve three accesses to the loop control variable to initialise, increment and test it for (i=0; i < 10; i++); in languages that support usage of the form for (i in v_list) only one access is required; in languages with vector operations many loops are implicit.
It is possible that application and language issues will change the absolute number of accesses but not effect their distribution. More measurements are needed.
Recent Posts
Recent Comments
Tags
Archives
- December 2024
- November 2024
- October 2024
- September 2024
- August 2024
- July 2024
- June 2024
- May 2024
- April 2024
- March 2024
- February 2024
- January 2024
- December 2023
- November 2023
- October 2023
- September 2023
- August 2023
- July 2023
- June 2023
- May 2023
- April 2023
- March 2023
- February 2023
- January 2023
- December 2022
- November 2022
- October 2022
- September 2022
- August 2022
- July 2022
- June 2022
- May 2022
- April 2022
- March 2022
- February 2022
- January 2022
- December 2021
- November 2021
- October 2021
- September 2021
- August 2021
- July 2021
- June 2021
- May 2021
- April 2021
- March 2021
- February 2021
- January 2021
- December 2020
- November 2020
- October 2020
- September 2020
- August 2020
- July 2020
- June 2020
- May 2020
- April 2020
- March 2020
- February 2020
- January 2020
- December 2019
- November 2019
- October 2019
- September 2019
- August 2019
- July 2019
- June 2019
- May 2019
- April 2019
- March 2019
- February 2019
- January 2019
- December 2018
- November 2018
- October 2018
- September 2018
- August 2018
- July 2018
- June 2018
- May 2018
- April 2018
- March 2018
- February 2018
- January 2018
- December 2017
- November 2017
- October 2017
- September 2017
- August 2017
- July 2017
- June 2017
- May 2017
- April 2017
- March 2017
- February 2017
- January 2017
- December 2016
- November 2016
- October 2016
- September 2016
- August 2016
- July 2016
- June 2016
- May 2016
- April 2016
- March 2016
- February 2016
- January 2016
- December 2015
- November 2015
- October 2015
- September 2015
- August 2015
- July 2015
- June 2015
- May 2015
- April 2015
- March 2015
- February 2015
- January 2015
- December 2014
- November 2014
- October 2014
- September 2014
- August 2014
- July 2014
- June 2014
- May 2014
- April 2014
- March 2014
- February 2014
- January 2014
- December 2013
- November 2013
- October 2013
- September 2013
- August 2013
- July 2013
- June 2013
- May 2013
- April 2013
- March 2013
- February 2013
- January 2013
- December 2012
- November 2012
- October 2012
- September 2012
- August 2012
- July 2012
- June 2012
- May 2012
- April 2012
- March 2012
- February 2012
- January 2012
- December 2011
- November 2011
- October 2011
- September 2011
- August 2011
- July 2011
- June 2011
- May 2011
- April 2011
- March 2011
- February 2011
- January 2011
- December 2010
- November 2010
- October 2010
- September 2010
- August 2010
- July 2010
- June 2010
- May 2010
- April 2010
- March 2010
- February 2010
- January 2010
- December 2009
- November 2009
- October 2009
- September 2009
- August 2009
- July 2009
- June 2009
- May 2009
- April 2009
- March 2009
- February 2009
- January 2009
- December 2008
Interesting concept, I never thought of studying that.
It isn’t clear what you are trying to optimize here, but in terms of making the program execute faster, there will be some highly nonlinear jumps involved. For example, the most common CPU architecture (i386) has about 8 registers, not all of which are general purpose. So providing a chunk of code can keep the number of local variables down to a single digit, the compiler can register everything and access is essentially instantaneous (or as fast at that CPU could process those instructions in any case).
Once there are too many variables to fit into registers, the compiler must choose some to spill onto the stack. As you point out, there tends to be a small number of variables that are accessed a large number of times, so presuming the compiler is smart, those would be in registers and their influence on run speed is zero. However, the big jump comes when variables end up on the stack because access to real memory is slow.
It gets even more complicated because of the cache. My gut feeling is that the middle section of the curve is the bit that has the biggest influence.
By the way, as CPU’s get faster, optimizing algorithms is becoming moot. You may iterate 100 times to get an answer, but the answer is still gets there faster than anything else you can do, so don’t worry too much.
Hmmm, that seems a bit unfair. Maybe you are arguing that good looking and easily readable source code is an advantage (fair enough) but for example, java has some nice iteration syntax, which is clean at the source-code level; but with huge and menacing machinery under the hood. A whole loop iteration object gets created to hold the loop variable and functions get called against that object.
Again, with CPU power growing faster than anyone knows what to do with it, many people are happy writing clean source code, and so long as the machinery works they don’t care. But in that case, counting a java iterator as only one read access is ridiculous.
If you are trying to measure the overall readability of source code and productivity of the programmer (ignoring runtime execution efficiency), then your metrics don’t seem appropriate for that (and all metrics of programmer productivity tend to be arguable).