Randomizing a list of items using sort() and rand()
I’m busy putting together the experiment I will be running at the ACCU conference next week. If you are attending the conference please reserve your Thursday lunchtime slot for taking part as a subject!
Experiment generation invariably involves randomizing the sequence of items seen by every subject. While few languages support a randomise function many support sorting and random number generation. These two functions can be combined to create a randomize function; simply append a random number to the start of each item, sort it and then strip off the random number. Voilà a randomized list (awk code below).
function rand_items(items) { for (v in items) { items[v]=rand() " " items[v] } asort(items) for (v in items) { sp_pos=index(items[v], " ") items[v]=substr(items[v], sp_pos+1) } } |
This randomization problem is not yet listed on Rosetta code and probably has longer solutions in other languages.
Update (the next day).
The glow I have had for the last 10 years over coming up with a neat solution to a problem has now disappeared. Following the link kindly provided by D. Herring in the comments eventually lead me to the Fisher-Yates shuffle, which has 
performance (the call to sort is probably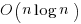 
. The following shuffles a deck of cards:
for (i = 0; i < 52; i++) { j = i + (rand() % (52 - i)); tmp = card[i]; card[i] = card[j]; card[j] = tmp; } |
The proof of the uniform shuffling behavior of Fisher-Yates (also known as Knuth shuffle) is straight forward but not nearly as appealing as using rand and sort.
Using a similar idea you can randomly select N elements from a stream of elements of unknown size if you keep the N biggest values (after you prepend the random numbers).
For each element
…prepend random number
…if the new value is bigger than any of the saved values, replace the smallest saved value with this value.
strip N saved values of prefix
return the N saved values
So you don’t need to know the size of the stream/list you are reading, you will always have N randomly sampled elements as long as you read N elements 🙂
Here’s the same algorithm in CL, circa 2008.
http://www.pvk.ca/Blog/Lisp/trivial_uniform_shuffling.html
I look forward to reading about your latest ACCU experiment. The results are usually quite interesting.
@D Herring
Thanks for the link which lead me to the Fisher-Yates shuffle and an update to the post.
The standard C++ library has random_shuffle() in the algorithm include file, which is O(n).
random_shuffle(v.begin(), v.end());
which I suppose would be random_shuffle(begin(v), end(v)); in the new-fangled C++11. There’s a also an override where you can supply your own RNG.
@Magnus
Yes, it has been there since C++99. These days there are freely available libraries for doing almost everything. I guess my post should have said something like “if you are using a language that does not easily support linking against third party libraries (awk in my case) here is a useful technique”.
The Knuth (a.k.a. Fisher-Yates shuffle) is on Rosetta Code here: http://rosettacode.org/wiki/Knuth_shuffle
If you’re using C, you probably don’t want to use rand() : it’s a very poor random-number generator. (For example, on many implementations the least significant bit of rand()s result is either constant, or just tlggles bacn and forth between 0 and 1 with each successive call.) random() or drand48() are much better.