Archive
Using Coccinelle to match if sequences
I have been using Coccinelle to obtain measurements of various properties of C if and switch statements. It is rare to find a tool that does exactly what is desired, but it is often possible to combine various tools to achieve the desired result.
I am interested in measuring sequences of if-else-if statements and one of the things I wanted to know was how many sequences of a given length occurred. Writing a pattern for each possible sequence was the obvious solution, but what is the longest sequence I should search for? A better solution is to use a pattern that matches short sequences and writes out the position (line/column number) where they occur in the code, as in the following Coccinelle pattern:
@ if_else_if_else @ expression E_1, E_2; statement S_1, S_2, S_3; position p_1, p_2; @@ if@p_1 (E_1) S_1 else if@p_2 (E_2) S_2 else S_3 @ script:python @ expr_1 << if_else_if_else.E_1; expr_2 << if_else_if_else.E_2; loc_1 << if_else_if_else.p_1; loc_2 << if_else_if_else.p_2; @@ print "--- ifelseifelse" print loc_1[0].line, " ", loc_1[0].column, " ", expr_1 print loc_2[0].line, " ", loc_2[0].column, " ", expr_2 |
noting that in a sequence of source such as:
if (x == 1) stmt_1; else if (x == 2) stmt_2; else if (x == 3) stmt_3; |
the tokens if (x == 2) will be matched twice, the first setting the position metavariable p_2 and then setting p_1. An awk script was written to read the Coccinelle output and merge together adjacent pairs of matches that were part of a longer if-else-if sequence.
The first pattern did not concern itself with the form of the controlling expression, it simply wrote it out. A second set of patterns was used to match those forms of controlling expression I was interested in, but first I had to convert the output into syntactically correct C so that it could be processed by Coccinelle. Again awk came to the rescue, converting the output:
--- ifelseifelse 186 2 op == FFEBLD_opSUBRREF 191 7 op == FFEBLD_opFUNCREF --- ifelseifelse 1094 3 anynum && commit 1111 8 ( c [ colon + 1 ] == '*' ) && commit |
into a separate function for each matched sequence:
void f_1(void) { // --- ifelseifelse /* 186 2 */ op == FFEBLD_opSUBRREF ; /* 191 7 */ op == FFEBLD_opFUNCREF ; } void f_2(void) { // --- ifelseifelse /* 1094 3 */ anynum && commit ; /* 1111 8 */ ( c [ colon + 1 ] == '*' ) && commit ; } |
The Coccinelle pattern:
@ if_eq_1 @ expression E_1; constant C_1, C_2; position p_1, p_2; @@ E_1 == C_1@p_1 ; E_1 == C_2@p_2 ; @ script:python @ expr_1<< if_eq_1.E_1; const_1 << if_eq_1.C_1; const_2 << if_eq_1.C_2; loc_1 << if_eq_1.p_1; loc_2 << if_eq_1.p_2; @@ print loc_1[0].line, " ", loc_1[0].column, " 3 ", expr_1, " == ", const_1 print loc_2[0].line, " ", loc_2[0].column, " 2 ", expr_1, " == ", const_2 |
matches a sequence of two statements which consist of an expression being compared for equality against a constant, with the expression being identical in both statements. Again positions were written out for post-processing, i.e., joining together matched sequences.
I was interested in any sequence of if-else-if that could be converted to an equivalent switch-statement. Equality tests against a constant is just one form of controlling expression that meets this requirement, another is the between operation. Separate patterns could be written and run over the generated C source containing the extracted controlling expressions.
Breaking down the measuring process into smaller steps reduced the amount of time needed to get a final result (with Coccinelle 0.1.19 the first pattern takes round 70 minutes, thanks to Julia Lawall‘s work to speed things up, an overhead that only has to occur once) and allows the same controlling expression patterns to be run against the output of both the if-else-if and if-if patterns.
At the end of this process I ended up with a list information (line numbers in source code and form of controlling expression) on if-statement sequences that could be rewritten as a switch-statement.
GLR parsing is the future
Traditionally parser generators have required that their input grammar be LALR(1) or some close variant (I would include LL(1) in this set). Back when 64k was an unimaginably large amount of memory being able to squeeze parser tables in a few kilobytes was very important; people received PhDs on parser table compression.
There is still a market for compact, fast parsers. Formal language grammars abound in communication protocols and vendors of communications hardware are very interested in keeping down costs by using minimizing the storage needed by their devices.
The trouble with LALR(1) is that value 1. It means that the parser only looks ahead one token in the input stream. This often means that a grammar is flagged as being ambiguous (i.e., it contains shift/reduce or reduce/reduce conflicts) when it is actually just locally ambiguous, i.e., reading tokens further head on the input stream would provide sufficient context to unambiguously specify the appropriate grammar production.
Restructuring a grammar to make it LALR(1) requires a lot of thought and skill and inexperienced users often give up. I once spent a month trying to remove the conflicts in the SQL/2 grammar specified by the SQL ISO standard; I managed to get the number down from over 1,000 to a small number that I decided I could live with.
It has taken a long time for parser generators to break out of the 64k mentality, but over the last few years it has started to happen. There have been two main approaches: 1) LR(n) provides a mechanism to look further ahead than one token, ie,
I think that GLR parsing is the future for two reasons:
- It is supported by the most widely used parser generator, bison.
- It enables working parsers to be created with much less thought and effort than a LALR(1) parser. (I don’t know how it compares against LR(n)).
GLR parsers resolve any language ambiguities by effectively delaying decisions until runtime in the hope that reading enough tokens will resolve local ambiguities. If an ambiguity in the token stream cannot be resolved a runtime error occurs (this is the one big downside of a GLR parser, the parser generated by a LALR(1) parser generator may produce lots of build time warnings but never produces errors when the parser is executed).
One example of a truly ambiguous construct (discussed here a while ago) is:
x * y; |
which in C/C++ could be a declaration of y to be a pointer to x, or an expression that multiplies x and y.
Tools that can detect these global ambiguities in a grammar are starting to appear, e.g., DTWA is a bison extension.
I reviewed an early draft of the new O’Reilly book “flex & bison” and tried to get the author to be more upbeat on GLR support in bison; I think I got him to be a bit less cautious.
To if-else-if or if-if, that is the question
I am currently measuring if-statements, occurring in visible source, that might be mapped to an equivalent switch-statement. The most obvious usage to look for is a sequence of if-else-if statements that all involve the same expression being tested against an integer constant, as in
if (x == 1) stmt_1; else if (x == 2) stmt_2; else if (x == 3) stmt_3; |
Another possible sequence is:
if (x == 1) stmt_1; if (x == 2) stmt_2; if (x == 3) stmt_3; |
provided all but the last conditionally executed arms do not change the value of the common control variable (e.g., x).
I started to wonder about what would cause a developer to chose one of these forms over the other. Perhaps the if-if form would be used when it was obvious that the common conditional variable was not modified in the conditionally executed arm. This would imply that there would be more statements in the arms of if-else-if sequences than if-if sequences. The following plot of percentage occurrence (over all detected if-else-if/if-if forms) of line number difference between pars of associated if-statements (e.g., when the controlling expression occurs on line
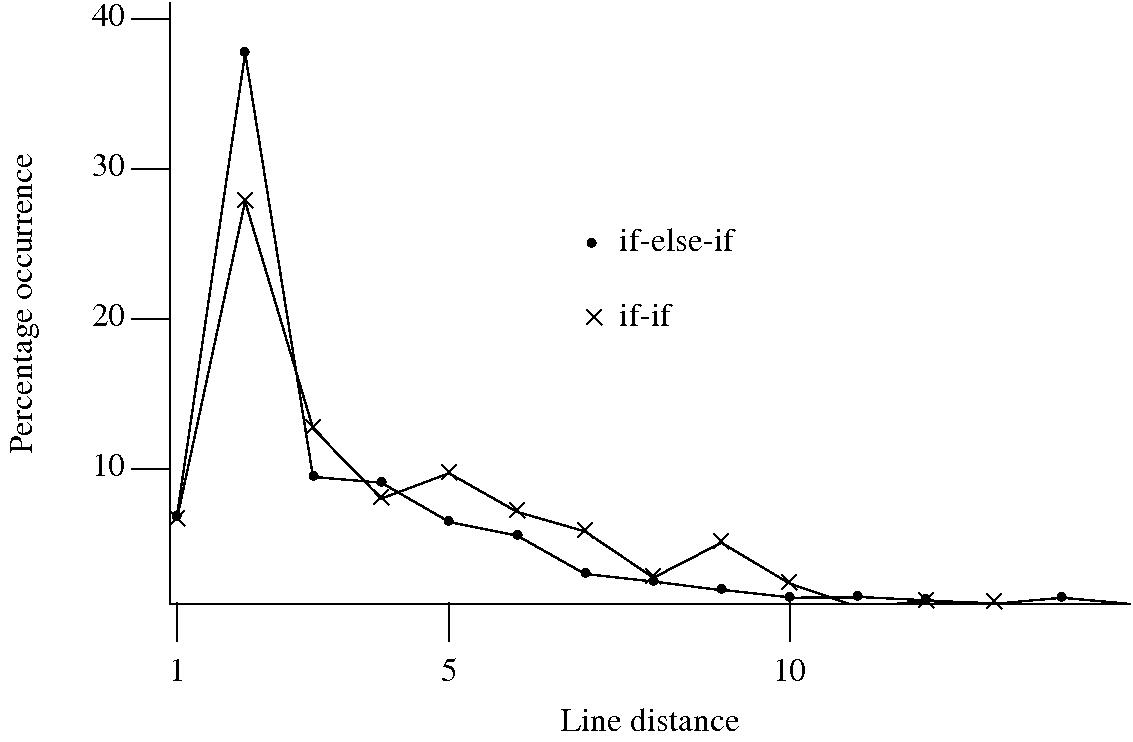
Just over a quarter of the arms contain a single statement (or to be exact the code is contained on a single line); this suggests that when using the if-else-if form most developers put the else and if on the same line. At the next distance along the percentage of if-else-if forms is twice as great as the if-if, probably because of else and if appearing on separate lines (as in the introductory example) in one case and less frequently a comment/blank line in the other. Next along, why the big increase in if-if forms? A comment + blank line, or perhaps no comment or blank line but the use of curly brackets (this is too off the track of where I am supposed to be going to investigate).
This morning I realized why the original plot did not look right, one of the data sets was a way off adding to 100%. An updated version has been uploaded.
It turns out that a single statement (or at least a single line) is more common in the if-else-if form, the opposite of what I had expected. At slightly larger distances there are still differences that can be attributed to else and if appearing on separate lines, curly brackets and a comment/blank line, but the effect is not as large as seen in the original, less accurate, plot.
I have a feeling that I ought to say something about the if-else-if form being preferred to the if-if form. One of the forms will have its behavior changed if the common control variable is modified in one of its arms. But is this an intended or unintended behavior? What is the typical characteristic usage of a common control variable, e.g., do they tend to be accessed but not modified in a given function definition? At the moment I see no obvious cost or benefit strongly favoring one usage over the other, so I will remain silent on the issue.
Recent Comments