Home > Uncategorized > Ternary radix will have to wait for photonic computers

Ternary radix will have to wait for photonic computers

July 9, 2012 Leave a comment Go to comments

Computer cpu economics suggest that a ternary radix representation rather than binary should be used for representing integer values. The economic cost of a cpu is is roughly proportional to 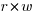r*w, where 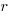r is the integer radix and 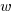w is the width, in bits, of the basic integer type (for simplicity I’m assuming there is only one and that the bus width has the same value); the maximum value that can be represented is r^w.

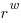If we fix the maximum representable value 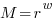M = r^w and ask which value of 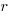r minimises 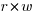r*w, then we need to differentiate 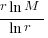{r ln M}/{ln r} w.r.t. 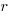r, giving 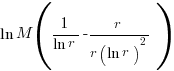ln M (1/{ln r} - r/{r (ln r)^2}) and this equals 0 when 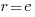r = e (the closest integer to 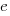e is 3).

The following plot shows the maximum representable value (right point of horizontal line) that can be achieved for a given ‘cost’ when the radix is 2 and 3.

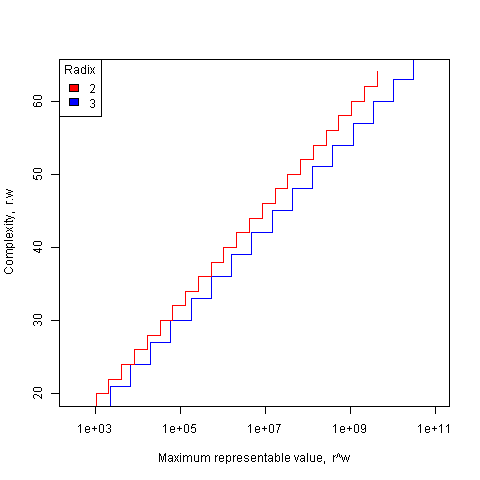
Binary/Ternary complexity vs maximum representable value

The reason binary is used in practice is purely to do with the characteristics of power consumption in electronic switching circuits (originally vacuum tube and then transistor based). Electrical power is proportional to voltage times current and a binary circuit can be implemented by switching between states where either the voltage or the current is very small, in either of these two states the power consumption is very low; it is only during the very short transition period switching between them, when the voltage and current have intermediate values, that the power consumed is relatively high. A 3-state switch would need a voltage/current combination denoting a state other than 0/1, and any such combination would consume non-trivial amounts of power (tri-state devices are used in some situations).

I have little idea about the complications of storing ternary values in memory systems, but I guess there will be complications.

In the 1960’s the Setun computer used a ternary radix and there has been the odd experimental systems since.

Are there any kinds of switching circuit whose use is not primarily dictated by device power characteristics and hence might be used to support a ternary radix? One possibility is a light based cpu (i.e., using photons rather than electrons), using polarization to specify state has been proposed. What about storage? Using Josephson junctions could provide the high speed and low power consumption required (we just need somebody to discover a room temperature superconductor).

The technology needed to build a practical cpu using a ternary radix appears to be some years in the future.

What about all the existing code containing a myriad of dependencies on the characteristics of two’s complement integer representation? If a photonic cpu became available that was ten times faster than existing cpus, or consumed 10 times less power or some combination thereof, then I’m sure here would be plenty of economic incentive to get software running on it. The problem is that 10 times better cpus are unlikely to just turn up, they will probably need to be developed in steps and the economics of progressing from step to step don’t look good.

While our civilization is likely to continue on down the binary rabbit hole, another one may have started down, or switched to, the ternary hole. I hope the SETI people are not to blinkered by the binary view of the universe.

Categories: Uncategorized Tags: , , , , , , ,
  1. anon
    July 9, 2012 22:27 | #1
    Reply | Quote

    Could be a scaling issue, but the chart you included makes it look as though the benefit from switching to ternary is pathetic. Binary is more convenient to work with and think about, just because of XOR if for absolutely no other reason, and I don’t think that’s just a result of our growing up with and being used to it. Those CPU speeds would have to *really* defy expectations before anyone would take the ternary idea seriously.

  2. Derek-Jones
    July 9, 2012 23:10 | #2
    Reply | Quote

    @anon
    The log scale on the x-axis does make ratios hard to judge. They are roughly a factor of 2 for 16-bit (binary equivalent) and factor of 4 for 32-bit. I suspect the Russians used ternary for the Setun because of severe component shortages. There might be a niche market for ternary in applications where component count is crucial.

    The figure was created using the following R code:

    w=seq(6, 32)
m3=3^w
m2=2^w
 
par(las=1)
 
plot(m3, w*3, log="x", xlim=c(3e2, 1e11), ylim=c(20, 64),
                type="s", col="blue", xlab="Maximum representable value,  r^w", ylab="Complexity,  r.w")
par(new=TRUE)
plot(m2, w*2, log="x", xlim=c(3e2, 1e11), ylim=c(20, 64),
                type="s", col="red", xlab="Maximum representable value,  r^w", ylab="Complexity,  r.w")
legend("topleft", legend=as.character(c(2, 3)),
       title="Radix", fill=c("red", "blue"))
  1. No trackbacks yet.